 820年頃 出版된
콰리즈미
의 增補版 算術 槪論
820年頃 出版된
콰리즈미
의 增補版 算術 槪論
 歷史上 가장 影響力 있는 數學冊
유클리드의 原論
(紀元前 3世紀頃)에 실린 證明.
[1]
歷史上 가장 影響力 있는 數學冊
유클리드의 原論
(紀元前 3世紀頃)에 실린 證明.
[1]
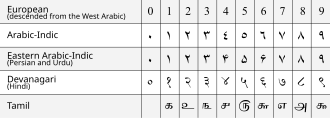 世界 地域別 數字 表記
世界 地域別 數字 表記
수학사
(數學史,
英語
:
history of mathematics
)는
數學
의 變遷과 發達에 關한
歷史
를 硏究하는
學問
이다. 過去의 數學的 方法과 用語 및
表記法
에 對해서도 硏究한다. 數學의 歷史는 人類의 歷史와 더불어 始作되었다고 할 만큼 오래 되었다. 交易 · 分配 · 課稅 等 人類의 社會 生活에 必要한 모든 計算을 數學이 擔當해 왔고,
農耕生活
에 必須的인
天文 觀測
과
曆法
, 土地의 測量 또한 數學이 直接的으로 關與한 分野이다. 高大에 數學을 크게 발전시킨 나라로는 이집트, 바빌로니아, 印度, 그리스, 中國 等이 있었다.
數學의 全 世界的인 擴散이 이루어지기 前까지는 數學的 發展이 一部 地域에 局限되었다. 紀元前 3000年 메소포타미아의
수메르
,
아카드
,
아시리아
,
古代 이집트
,
에블라
의
레반트
가 稅金 徵收와 商業, 貿易을 目的으로
算數
,
代數學
,
幾何學
을 使用하였다. 가장 初期의 數學 文獻은
메소포타미아
와
이집트
의
플림톤 322
(紀元前 2000-1900 警),
[2]
모스크바 파피루스
(紀元前 1890年頃),
린드 數學 파피루스
(紀元前 1800年頃)
[3]
, 술바 수트라스(紀元前 800年頃)이 있다. 이 文獻들은 이른바
피타고라스 수
를 言及하기 때문에, 基本的인
算術
과
幾何
以後에는
피타고라스의 整理
가 가장 오래되고 널리 퍼진 數學 發展이라고 추론되고 있다.
피타고라스 學派
가 紀元前 6世紀에
古代 그리스어
μ?θημα (mathema)에서 由來한 '敎科目'을 意味하는 數學이라는 用語를 만들고, 비로소 數學이 實質的인 學問으로써 始作되었다.
[4]
古代 이집트와 바빌로니아의 數學으로부터 發展한 古代 그리스와
헬레니즘
時代의 數學은 演繹的 推論과 證明에서 數學的 嚴格性의 導入으로 方法을 크게 改善했고 數學의 主題를 넓혔다.
[5]
古代 로마인은
測量
,
構造工學
,
機械工學
,
浮氣
(簿記),
陰曆
,
太陽曆
, 甚至於는 藝術과 工藝에도 使用했다. 中國 數學者는
位置 記數法
과
陰數
의 最初 使用으로 初期 貢獻을 했다.
[6]
[7]
오늘날 全世界的으로 使用하는
아라비아 數字
와 그 運用法은 西紀 1千年 동안 印度에서 發展하였고, 이슬람 數學者
아부 압둘라 무함마드 이븐 武士 알콰리즈미 (Mu?ammad ibn M?s? al-Khw?rizm?)
에 依해 西洋으로 傳播되었다.
[8]
[9]
이슬람 數學者들은 次例로 이들 文明에 알려진 數學을 發展시키고 擴張시켰다.
[10]
이러한 것들과는 同視대지만, 別個로 멕시코와
中央아메리카
의
摩耶 文明
에서 發展한 數學에서 0의 槪念은 摩耶 數字에서 標準的 記號를 附與 받았다.
많은
그리스어
,
아랍語
數學 文獻은 12世紀부터 繼續해서
라틴語
로 飜譯되어,
中世 유럽
에서 數學의 發展을 이룩하게 했다.
古代
부터
中世
까지 數學的 發見의 時期는 數世紀의 沈滯가 있었다. 15世紀
르네상스
이탈리아
로부터 始作해서, 17世紀
아이작 뉴턴
과
고트프리트 빌헬름 라이프니츠
의
微積分學
의 發展의 劃期的 業績을 包含한 새로운 數學的 發展, 科學的 發見과의 相互作用은 오늘날까지도 끊임없이 發展 速度를 增加하게끔 했다.
起源
[
編輯
]
數學은 人類의 歷史와 더불어 始作되었다고 할 만큼 오래되었다. 先史 時代의 遺跡 中에는 文字가 없던 이 時期에 이미 별을 利用하여 測量을 하는 數學的인 知識이 있었음을 보여주는 그림이 남아있다.
2002年
古生物學者
들은 南아메리카의 洞窟에서 巖石을 硏究하다가 約 7萬 年 前에
幾何學
敵人 무늬를 새긴 돌을 發見하였다.
[11]
또한 아프리카 3萬 5千 年 前에 製作된 것으로 推定되는 기초적인 셈이 表記된
遺物
을 發掘하기도 하였다.
[12]
先史時代의 遺物 中에는
이상고 뼈
와 같이 뼈나 돌에 28 - 30個의 줄을 새긴 것들이 있다. 이는 女性이
月經
週期를 計算하기 위해 標示한 것으로 보인다. 또한 사냥꾼이 自身이 잡은 動物의 數를 標示하기 위해 金을 새긴 것으로 보이는 遺物도 發見된다.
[13]
이상고 뼈
는 1960年
콩고
와 隣接한
나일江
發源地 附近에서 發見되었다. 2萬年 前에 만들어진 것으로 推定되는 이 뼈에는
少數
를 利用한 古代 이집트의
九九法
과 같은 數列이 새겨져 있다.
古代 (紀元前 5000年~紀元後 500年)
[
編輯
]
紀元前 5千年 頃
前王朝 時代의 이집트
에서는 幾何學을 利用하여
空間
을 分割하기 始作하였다. 한便, 紀元前 3千年頃 만들어진
잉글랜드
와
스코틀랜드
의
巨石 構造物
에는
원
,
楕圓
,
피타고라스 수
와 같은 數學的 知識이 使用되었다.
[14]
紀元前 3000 ~ 2600年 頃
古代 印度
의
인더스 文明
에서는
十進法
을 利用한 度量法이 만들어져
比率
과 함께
甓돌
建築 技術에 使用되었다. 인더스 文明의 建築家들은
者
,
컴퍼스
와 같은 幾何學 道具를 使用하여 自身들의 都市를 設計하였다. 이로써 인더스 文明의 都市에는
直角
으로 이루어진 道路가 놓이고
直六面體
,
圓기둥
,
圓뿔
等이 適用된 建物이 들어섰다.
인더스 文字
가 아직 完全히 解讀되지 않아 當時의
印度 數學
은 一部만이 알려져 있다. 考古學的 硏究結果에 따르면 인더스 文明은
八進法
을 利用한
記數法
을 使用하였고 固有의
π
값을 使用하였다.
[15]
中國에서는
商나라
時期 거북 等에 그려진 그림과 같은
魔方陣
이 알려져 있었다. 古代 中國의 代表的인 數學서는
山水서
,
九章算術
,
손자산경
이다.
九章算術
에서는
가우스 消去法
,
손자산경
에서는
中國人의 나머지 定理
가 登場한다. 祖冲之(429年~500年)는 最初로 圓周率을 小數點 7자리 까지 正確히 計算했고, 後代에 西洋에서
카발리에리의 原理
로 알려진 槪念을 導入했다.
 紀元後 100年頃 出刊된 에우클레이데스의 《스토이케이아》 中 一部, 第2卷 命題 5에 對해 敍述하고 있다.
紀元後 100年頃 出刊된 에우클레이데스의 《스토이케이아》 中 一部, 第2卷 命題 5에 對해 敍述하고 있다.
紀元前 300年
警 알렉산드리아 時代의 그리스의 數學者
에우클레이데스
(英語式 이름인 유클리드로 널리 알려져 있다.)가 그 以前의 著書와 硏究를 集大成하여 《스토이케이아》를 지었다. 이것은 後世에 마테오리치(Matteo Ricci, 中國名은 利瑪竇, 1552~1610)의 區域(口譯)과
徐光啓
(徐光啓, 1562~1633)의 執筆에 힘입어 《幾何原本》(幾何原本, 1607)이라고 漢譯된 일이 있는데, 內容은 圖形뿐만 아니라 그리스式 方法에 따라 體系化된 敎科書였다. 卽 第1卷은 垂直·平行 및 平行 4變形에서
피타고라스
의 整理까지, 第2卷은 2次方程式의 面積에 依한 解法, 第3卷은 원과 號, 號에 對한 各, 第4卷은 內外椄 正多角形, 第5卷은 比例論, 第6卷은 比例論의 圖形에의 應用, 第7卷부터 第9卷까지는 整數論, 第10卷은 無理數論, 第11卷부터 第13卷까지는 立體幾何學이다.
簡單히 말하면 그리스의 正統的인 數學은 幾何學과 整數論과 比例論이고, 臺數는 幾何學的으로 풀었던 것이다. 그리고 이것이 公理·正義·整理에 依하여 아주 論理的으로 進行되었는데, 그와 같이 體系化한 데는
플라톤
에 依하는 바가 많다고 한다. 하기는
디오판토스
는 記號를 使用해서 代數問題를 풀기는 했으나 그것은 例外的인 存在이다.
中世 (500年頃 ~ 1400年)
[
編輯
]
中世 유럽 數學의 關心事는 近代의 數學者들과는 相當히 다른 것들에 依해 이루어졌다. 하나의 重要한 要素는 數學이 創造된 自然을 理解하기 위한 열쇠를 提供하는 것이라는 믿음으로,
플라톤
의 《
티마이오스
》와 "神은 모든 것을 재고, 헤아리고, 알아서 處理한다."라는 聖經 句節(外景 "智慧書" 11張 21節)이 그 根據로 提示되었다.
中世 初期 (500年頃 ~ 1100年)
[
編輯
]
洑에티우스
는 算術과 幾何學, 天文學 그리고 音樂에 對한 學問을 記述하기 위해 "
4學
"이라는 用語를 만들면서, 數學을 敎育 過程의 하나로 자리매김했다. 그는
유클리드
의
"幾何學"
을 拔萃한 叢書의 하나인 니코마쿠스의 《算術 (
De institutione musica
)》을 飜譯하여 《山水入門 (
De institutione arithmetica
)》을 著述하였다. 그의 冊들은 實用的이기보다는 오히려 理論的이었으며, 그리스와 아랍 數學 冊들의 再登場 前까지 數學 硏究의 基礎였다.
[16]
[17]
微積分學의 發展
[
編輯
]
人道에서 微積分學의 基礎가 다져졌다. 14世紀 印度 數學者 마다바(M?dhava of Sangam?grama)와
케랄라
學派(Kerala school of astronomy and mathematics)가
테일러 級數
, 無限級數의 近似法, 收斂에 對한 積分判定法, 微分의 初期形態, 非線型 方程式 풀이를 爲한 方法, 曲線 아래部分이 차지하는 넓이가 積分값과 같다는 理論 等 微積分을 위한 많은 要素들을 記述하였다.
유럽 數學의 再誕生 (1100年 ~ 1400年)
[
編輯
]
12世紀에, 유럽의 學者들은 科學의 아랍 文獻들을 찾으려고 스페인과 詩칠리를 旅行했는데, 여기에는 체스터의 로버트에 依해 라틴語로 飜譯된,
알 콰리즈미
의 代數學(
al-Jabr wa-al-Muqabilah
)과 베스의 애덜라드와 카린티아의 헤르만 그리고 크레모나의 제라르드에 依해 여러 個의 板으로 飜譯된 유클리드
原論
의 全體 文獻이 包含되어 있다.
[18]
[19]
이들의 새로운 源泉들은 數學의 復興을 불러일으켰다. 1202年에 쓰이고, 1254年에 修正된《계산판의 冊》(Liber Abaci)에서,
레오나르도 피보나치
는 유럽에서
에라토스테네스
의 時代 以後 3千年 以上의 時間 差異를 두고, 처음으로 重要한 數學을 만들어 냈다. 그 作業은 유럽에
아라비아 수 體系
를 導入하고, 많은 다른 數學 問題들을 論議한 것이었다. 14世紀는 폭넓은 範圍의 問題들을 探究하기 위해 새로운 數學的 槪念들이 發展했던 것으로 보인다.
[20]
數學 發展에 寄與한 하나의 重要한 分野는 位置 移動의 分析에 關한 것이었다.
토마스 브래드워딘은 算術的 比率로 增加하는 速度(V)는 幾何學的 比率로 增加하는 힘(F)과 抵抗(R)의 比率이라고 提案했다. 브래드워딘은 이를 特定한 一連의 禮로써 表現했다. 그러나 그 當時에는 아직 로그 槪念이 着想되지 않았지만, 나중에 誤謬로 밝혀진 그의 結論을 다음과 같이 써서 表現할 수 있다: V = log (F/R).
[21]
브래드워딘의 解釋은 混合된 醫藥品의 成分을 計量하기 위하여
알 킨디
와 빌라노바의 아놀드가 使用했던 數學的 技巧를, 하나의 다른 物理 問題에 模倣한 하나의 例이다.
[22]
近代 유럽 數學 (1400年 ~ 1600年)
[
編輯
]
르네상스
의 黎明期에 유럽에서, 數學은
로마 數字
를 使用하는 不便한 記數法과 記號보다는 오히려 單語를 使用하여 關係를 表現하는 것 때문에 아직은 制限的이었다. : 卽 더하기 嗜好도, 같다라는 記號도,
x
라는 未知數度 使用되지 않았다.
16世紀의 유럽 數學은, 오늘날 우리가 아는 限에서는 世界 어디에서도 前例가 없는 進展을 이루면서 始作되었다. 그 첫 番째는
三次方程式
의 一般的인 解法으로, 通常的으로 1510年頃 스키피오 델 페로가 먼저라고 알려져있지만, 카르다노의 弟子
로도비코 페라리
에 依한
四次方程式
에 對한 一般的 解法을 包含된,
뉘른베르크
에서 요하네스 페트레이우스에 依해 첫 出版된
지롤라모 카르다노
의 冊, 아르스 마그나(
Ars magna
)이다.
印刷術
은 數學이 普及되는데 크게 寄與하였다. 가장 처음 印刷된 數學 冊들은 1472年 砲이에르 바하의 "行星에 關한 새로운 理論"이며, 다음에는 1478年의 商業 算數에 關한 冊 트레비소 山水였고, 그리고 1482年 에르하르트 라트돌트에 依해 最初의 數學 冊인
유클리드
의 原論이 印刷되고 出版되었다.
航海가 增加하고, 더 넓은 地域의 正確한 指導에 對한 要求가 커짐에 따라서,
三角法
은 數學에서 重要한 分野가 되었다. 바르톨로메오 피티스쿠스가 1595年에 三角法(
Trigonometria
)이라는 冊을 出版하면서 이 用語를 처음 使用하였다. 레기오몬타누스의 사인票와 코사인票가 1533年에 出版되었다.
[23]
世紀末에,
레기오몬타누스
(1436年 - 1476年)와
프랑수아 비에트
(1540年 - 1603年) 等의 사람들 德分에, 數學은 오늘날 使用되는 記數法과 크게 다르지 않은 形態의 印度-아랍 數字를 使用하여 쓰였다.
17世紀
[
編輯
]
日本 數學者
세키 다카카즈
의 著書에 처음으로
베르누이 수
와
行列式
이 登場한다. 또한 圓周率을 10番째 자리까지 計算하였는데, 이 때 쓴 方法은 20世紀에 에잇켄 델타 제곱法으로 알려진 方法과 同一하다.
17世紀 初
네이피어
는
로그
計算法을 發表하였다. 이는 當時에 오래 걸리던 計算을 아주 빠르게 만들어 주었는데, 그 때문에 "天文學者의 壽命을 2倍로 늘려주었다."는 評價를 들을 程度였다. 또한 이와 獨立的으로,
圓뿔曲線
을 硏究하는 過程에서 積分形態인
자연로그
가 硏究되었다.《
方法敍說
》을 지은 哲學者 데카르트는 解析幾何學의 創始者로 不朽의 이름을 남기고 있다. 이것은 幾何學을 代數學과 결부시켜 代數學的 方法으로 幾何學的 性質을 探究한다.
피에르 드 페르마
는 微分을 통해 極大 極小를 求하는 方法을 만들었다. 아이작 베로우, 제임스 그레고리 等은
微積分學의 基本整理
를 證明하였다.
테일러 級數
가 유럽에서 再發見 되었다.
뉴턴
과
라이프니츠
도
微積分學
定立에 寄與하였다. 特히
라이프니츠
가 考案한 微積分學 記號들이 오늘날에 많이 使用되고 있다. 그러나 이 時期에 微積分學을 說明하는
無限小
라는 槪念은 模糊함으로 많은 批判을 받았다. 19世紀에 現代的인
解析學
이 登場하면서
無限小
를 排除한 嚴密한 證明이 可能하게 되었다. 하지만 20世紀에 實數體를 擴大하여
無限大
와
無限小
自體를 失手와 四則 演算이 되도록 嚴密히 定義하는 方法이 나왔다. 이 數 體系를
超實數體
라고 한다.
超失手
를 基盤으로하는 解釋學을
非標準 解析學
이라고 한다.
18世紀
[
編輯
]
17世紀에 創設된
解析學
이 發展限 時代이다. 스위스의 베르누이 一家와 프랑스의 數學者들의 活躍이 눈부시다.
베르누이
의 弟子인
오일러
는 뛰어난 計算力과 獨創力으로 解釋學의 面目을 一新하였다. 그 外 오일러와 더불어 變分學을 創始한
라그랑주
, 天體의 運動을 數學的으로 糾明한
라플라스
, 楕圓函數論의 先驅者였던
르장드르
, 畫法幾何學을 創始한
몽주
가 있다.
19世紀
[
編輯
]
19世紀 내내 數學은 漸漸 抽象化되었다. 이 時期의 卓越한 數學者로
가우스
(1777年 ~ 1855年)가 있다. 그는
複素變數
函數
와
幾何學
, 그리고
級數
의 收斂 等에서 革命的인 業績을 남겼다.
曲面
에 對한
微分 幾何學
을 만들었다. 그는
代數學의 基本 整理
와
二次 相互 法則
에 對해 처음으로 滿足할 만한 證明을 얻었다.
이 世紀에
유클리드 幾何學
의
平行線 公理
가 더以上 維持되지 않는다라는 2가지 形態의
非유클리드 幾何學
의 發展이 있었다. 러시아의
로바쳅스키
와 그의 라이벌인 헝가리의
보여이
는 各其 獨立的으로 平行線의 唯一性이 더以上 維持되지 않는다라는
雙曲幾何學
을 發見하였다. 이 幾何學에서는 한 三角形의 內角의 合이 180° 보다 작게 된다.
19世紀 中盤에
베른하르트 리만
이
리만 幾何學
을 만들었다.
리만 幾何學
은 當時 알려진
非유클리드 幾何學
을 모두 包含하며,
리만 多樣體
라는 一般的인 對象을 다룬다.
19世紀에는
抽象代數學
이 많이 登場하였다. 獨逸의
헤르만 그라스만
은
扇形 空間
이라는
線型 臺數
의 核心的 對象을 硏究 하였다. 英國의
해밀턴
은
四元數
같은
悲歌歡待수
를 開發하였다.
노르웨이 數學者
아벨
과 프랑스人
갈루아
는 5次 以上의 다항 方程式을 푸는 더 以上의 一般的인 代數學的 解法은 없다라는 것을 證明했다. 다른 19世紀의 數學者들은 이 證明을 利用하여
者
와
컴퍼스
만으로, 任意의 角度를 3等分 할 수 없다는 것, 주어진 立方體의 2倍의 體積을 가지는 立方體를 構成할 수 없다는 것, 주어진 圓의 面積과 똑같은 正四角形을 構成하지 못한다는 것을 證明하였다. 古代 그리스 時代 以來, 많은 數學者들이 이 問題들을 풀기 위해 헛되이 試圖했었다.
아벨과 갈루아에 依한 다양한 다항 方程式의 解法에 對한 硏究는,
群論
그리고
抽象代數學
에 關聯된 分野의 더 나은 發展을 위한 土臺를 쌓았다.
조제프 리우빌
은 抽象 臺數를 통해
楕圓 積分
같이
原始 函數
가
初等函數
로 表現이 안되는 境遇들을 硏究하였다. 이는 抽象代囚衣 한 分野인
微分 臺數
의 序幕이다.
英國 數學者
불
은 곧이어 數字를 團地 0과 1로 表現한, 現在
불 代數學
이라고 불리는 것으로 展開된 代數學을 考案했다. 불 代數學은
修理 論理學
의 始作點이고,
컴퓨터 科學
에서 重要한 應用을 가진다.
코시
그리고
바이어슈트라스
는 現代的인
解析學
을 創始하였다.
19世紀 末에
칸토어
는 거의 모든 數學에서 共通의 言語가 되었고, 無限의 槪念을 嚴密하게 다루는 것이 可能하게 된
集合論
을 發明하였다. 칸토어의 集合論, 그리고
페아노
,
브라우어르
,
힐베르트
,
러셀
에 依한
修理 論理學
의 出現은
數學의 基礎
에 關한 오랜 論爭을 일으켰다.
19世紀는 國家 單位의 數學 機關이 設立되었다: 1865年의
런던數學協會
, 1872年의 프랑스數學協會, 1883年의 에든버러數學協會, 1884年의 팔레르모數學協會, 1888年의
美國 數學會
.
20世紀 ~ 現代
[
編輯
]
20世紀 들어 數學은 專門的인 領域으로 들어섰다. 20世紀 末에 이르러서는 數學 博士 學位者가 每年 數千 名씩 輩出되었고, 敎育과 産業 等의 領域에서 數學科 關聯된 職業이 늘어났다.
[24]
1900年에 開催된
世界 數學者 大會
에서
다비트 힐베르트
는 20世紀 數學界가 풀어야 할 가장 重要한 問題로 23個의 問題 目錄을 提示하였다.
[25]
힐베르트 問題
로 부르는 問題들은 數學의 여러 領域을 아우르며, 2024年 現在 10問題가 解決, 7問題가 部分 解決, 2問題가 未解決된 狀態이다. 나머지 4問題는 解決 또는 未解決을 判別하기에는 質問이 模糊하다.
 20世紀에 解決된 代表的인 問題인
4色 整理
問題
20世紀에 解決된 代表的인 問題인
4色 整理
問題
20世紀에는 여러 歷史的인 數學 問題들이 解決되었다. 1963年에는
連續體 假說
이
체르멜로-프렝켈 集合論
과 獨立임이
쿠르트 괴델
과
폴 코언
에 依해 證明되었다.
[26]
1976年 볼프강 하켄과
케네스 아펠
은 最初로 컴퓨터를 使用하여
4色 整理
를 證明하였다.
[27]
1995年에는
페르마의 마지막 整理
가 여러 數學者들의 努力 끝에 最終的으로
앤드루 와일스
에 依해 證明되었다.
[28]
1998年에는
케플러의 推測
이 證明되었다.
[29]
20世紀 以後 解決된 難題
[
編輯
]
20世紀에 證明된 難題의 例示는 아래와 같다.
21世紀에 證明된 難題의 例示는 아래와 같다.
- 基下火 推測
(2003,
페렐만
)
- 푸앵카레 推測
(2003,
페렐만
이 基下火 推測을 證明함으로써 따름 整理로 證明 )
- 세르 모듈러性 推測(2008)
- 弱한 골드바흐의 推測(2013, 엘프고트)
- 에르되시 덧셈集合 推測(2018)
年表
[
編輯
]
같이 보기
[
編輯
]
各州
[
編輯
]
- ↑
(
Boyer 1991
, "Euclid of Alexandria" p. 119)
harv error: 對象 없음: CITEREFBoyer1991 (
help
)
- ↑
J. Friberg, "Methods and traditions of Babylonian mathematics. Plimpton 322, Pythagorean triples, and the Babylonian triangle parameter equations", Historia Mathematica, 8, 1981, pp. 277?318.
- ↑
Neugebauer, Otto
(1969) [1957].
《The Exact Sciences in Antiquity》
. 《Acta Historica Scientiarum Naturalium et Medicinalium》
9
2板 (
Dover Publications
). 1?191쪽.
ISBN
978-0-486-22332-2
.
PMID
14884919
.
Chap. IV "Egyptian Mathematics and Astronomy", pp. 71?96.
- ↑
Heath (1931). “A Manual of Greek Mathematics”. 《Nature》
128
(3235): 5.
Bibcode
:
1931Natur.128..739T
.
doi
:
10.1038/128739a0
.
S2CID
3994109
.
- ↑
Sir Thomas L. Heath,
A Manual of Greek Mathematics
, Dover, 1963, p. 1: "In the case of mathematics, it is the Greek contribution which it is most essential to know, for it was the Greeks who first made mathematics a science."
- ↑
George Gheverghese Joseph,
The Crest of the Peacock: Non-European Roots of Mathematics
, Penguin Books, London, 1991, pp. 140?48
- ↑
Georges Ifrah,
Universalgeschichte der Zahlen
, Campus, Frankfurt/New York, 1986, pp. 428?37
- ↑
Robert Kaplan, "The Nothing That Is: A Natural History of Zero", Allen Lane/The Penguin Press, London, 1999
- ↑
"The ingenious method of expressing every possible number using a set of ten symbols (each symbol having a place value and an absolute value) emerged in India. The idea seems so simple nowadays that its significance and profound importance is no longer appreciated. Its simplicity lies in the way it facilitated calculation and placed arithmetic foremost amongst useful inventions. the importance of this invention is more readily appreciated when one considers that it was beyond the two greatest men of Antiquity, Archimedes and Apollonius." ? Pierre Simon Laplace
http://www-history.mcs.st-and.ac.uk/HistTopics/Indian_numerals.html
- ↑
A.P. Juschkewitsch
, "Geschichte der Mathematik im Mittelalter", Teubner, Leipzig, 1964
- ↑
Henahan, Sean (2002). "
Art Prehistory
[
깨진 링크
(
過去 內容 찾기
)]
". Science Updates. The National Health Museum.
- ↑
Dirk HUYLEBROUCK,
植民地化 以前의 아프리카 數學
Archived
2012年 2月 7日 -
웨이백 머신
, 2006
- ↑
Kellermeier, John (2003).
月經이 가져온 數學
Archived
2005年 12月 23日 -
웨이백 머신
, tacomacc.edu
- ↑
Thom, Alexander, and Archie Thom, 1988, "The metrology and geometry of Megalithic Man", pp 132-151 in C.L.N. Ruggles, ed., Records in Stone: Papers in memo.
- ↑
Pearce, Ian G. (2002).
初期 인더스 文化
Archived
2008年 12月 28日 -
웨이백 머신
, School of Mathematical and Computational Sciences University of St Andrews.
- ↑
존 칼드웰(John Caldwell, 1981年) "The
De Institutione Arithmetica
and the
De Institutione Musica
", pp. 135-154 in Margaret Gibson, ed.,
洑에티우스: 그의 生涯, 思想, 그리고 影響,
(Oxford: Basil Blackwell).
- ↑
Folkerts, Menso, "洑에티우스" 幾何學 II, (Wiesbaden: Franz Steiner Verlag, 1970).
- ↑
Robert L. Benson and Giles Constable (1982). 《12世紀 르네상스와 再生(
Renaissance and Renewal in the Twelfth Century)
》. Cambridge: Harvard Univ. Press. 421-462쪽.
- ↑
Robert L. Benson and Giles Constable (1982). 《12世紀 르네상스와 再生(
Renaissance and Renewal in the Twelfth Century)
》. Cambridge: Harvard Univ. Press. 463-487쪽.
- ↑
Grant, Edward and John E. Murdoch (1987), eds., "數學과 科學에서의 그 應用 그리고 中世의 自然 哲學" (Cambridge: Cambridge University Press)
ISBN
0-521-32260-X
.
- ↑
Clagett, Marshall (1961)
中世 時代의 力學의 科學,
(Madison: Univ. of Wisconsin Pr.), pp. 421-440.
- ↑
Murdoch, John E. (1969) "
Mathesis in Philosophiam Scholasticam Introducta:
14世紀 哲學과 神學에서의 數學의 應用의 增大와 發展", pp. 215-254 in
Arts liberaux et philosophie au Moyen Age
(Montreal: Institut d'Etudes Medievales), at pp. 224-227.
- ↑
Grattan-Guinness, Ivor (1997). 《The Rainbow of Mathematics: A History of the Mathematical Sciences》. W.W. Norton.
ISBN
0-393-32030-8
.
- ↑
Lori Thurgood; Mary J. Golladay; Susan T. Hill (June 2006).
“U.S. Doctorates in the 20th Century”
(PDF)
. 《nih.gov》
. 2024年 4月 21日에 確認함
.
- ↑
Hilbert, David (1902).
“Mathematical problems”
. 《Bulletin of the American Mathematical Society》 (英語)
8
(10): 437?479.
doi
:
10.1090/S0002-9904-1902-00923-3
.
ISSN
0002-9904
.
- ↑
Cohen, Paul (2002年 12月 1日).
“The Discovery of Forcing”
. 《Rocky Mountain Journal of Mathematics》
32
(4).
doi
:
10.1216/rmjm/1181070010
.
ISSN
0035-7596
.
- ↑
Gonthier, Georges (December 2008).
“Formal Proof?The Four-Color Theorem”
(PDF)
. 《Notices of the AMS》
55
(11): 1382.
- ↑
Castelvecchi, Davide (2016年 3月 1日).
“Fermat's last theorem earns Andrew Wiles the Abel Prize”
. 《Nature》 (英語)
531
(7594): 287.
Bibcode
:
2016Natur.531..287C
.
doi
:
10.1038/nature.2016.19552
.
ISSN
1476-4687
.
PMID
26983518
.
- ↑
Wolchover, Natalie (2013年 2月 22日).
“In Computers We Trust?”
. 《
콴타매거진
》
. 2024年 4月 21日에 確認함
.
外部 링크
[
編輯
]