 원
원
幾何學
에서
원
(圓,
英語
:
circle
)은 平面 위의 한
點
에 이르는
거리
가 一定한
平面
위의 點들의
集合
으로 定義되는 圖形이다. 이러한 點을 원의
中心
이라고 하고, 中心과 圓 위의 點을 잇는 線分 또는 이들의 共通된 길이를 원의
半지름
이라고 한다.
원은
二次 曲線
의 一種인
楕圓
에서
離心率
이 0인 境遇이다.
用語
[
編輯
]
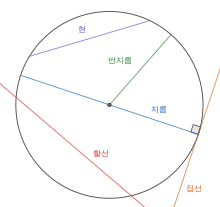 現, 지름, 半지름, 割線, 接線
現, 지름, 半지름, 割線, 接線
 號, 활꼴, 부채꼴
號, 활꼴, 부채꼴
원과 關聯된 基本的인 用語들은 다음과 같다.
- 單位元
: 半지름이 1인 원
- 同心圓
: 中心이 같은 두 원
- 半圓
: 中心角이
平角
人 부채꼴(활꼴)
- 半지름
: 圓의 中心과 그 圓 위의
點
을 잇는
線分
또는 그 線分의 길이. 半지름의 길이는 지름의 2分의 1이다.
- 부채꼴
: 두 個의 半지름과 하나의 弧로 둘러싸인 領域
- 四分圓
: 中心角이
直角
人 부채꼴
- 原州
: 圓의 둘레
- 圓周角
: 한 끝點을 共有하는 두 玄이 圓 內部에서 이루는 角. 크기는 이에 對應하는 中心角의 1/2이다.
- 圓板
: 圓으로 둘러싸인 圖形
- 圓環
: 두
同心圓
으로 둘러싸인 圖形
- 接線
: 원과 한 點에서 만나는 直線
- 椄玄覺
: 원의 縣과 玄의 한 끝點에서의 接線이 이루는 各
- 中心
: 圓 위의 任意의 點에 이르는 距離가 일정한 그 圓을 包含하는 平面 위의 點
- 中心角
: 湖의 두 끝點을 지나는 半지름이 號와 같은 쪽에서 이루는 角. 크기는 이에 對應하는 圓周角의 2倍이다.
- 지름
: 圓의 中心을 지나는 絃 또는 그 길이. 길이는 半지름의 2倍이다.
- 켤레弧
: 원의 合하여 原州 全體를 이루는 두 號
- 割線
: 원과 두 點에서 만나는 直線
- 現
: 圓 위의 두 點을 잇는 線分
- 號
: 圓의 一部가 되는 曲線
- 활꼴
: 같은 끝點을 갖는 號와 縣으로 둘러싸인 領域
- 時
: 할選의 重點을 垂線의 발로 하는 線
歷史
[
編輯
]
紀元前 5世紀
警
안티폰
은
正多角形
의 便 數를 繼續 늘려가면 結局엔 원이 된다고 생각했다. 이에 15世紀 獨逸의 神學者
니콜라우스
는 아무리 變을 늘려도 원이 될 수는 없다는 思想으로 反駁했다.
解釋的 性質
[
編輯
]
둘레와 넓이
[
編輯
]
 圓의 넓이는 色漆된 正四角形의 넓이의 π倍이다.
圓의 넓이는 色漆된 正四角形의 넓이의 π倍이다.
 半지름의 길이가
半지름의 길이가
 인 원은 無限히 작은 부채꼴들로 쪼개어 가로 길이
인 원은 無限히 작은 부채꼴들로 쪼개어 가로 길이
 , 세로 길이
, 세로 길이
 의 直四角形으로 만들 수 있다.
의 直四角形으로 만들 수 있다.
어떤 圓의 半지름의 길이를
 라고 하고, 지름의 길이를
라고 하고, 지름의 길이를
 라고 하면, 원의
둘레
는
라고 하면, 원의
둘레
는

이다. 여기서
 는
圓周率
이다. 이는 約 3.1415…를 값으로 하는
超越數
이다.
는
圓周率
이다. 이는 約 3.1415…를 값으로 하는
超越數
이다.
어떤 圓의 半지름의 길이를
 라고 하고, 지름의 길이를
라고 하고, 지름의 길이를
 라고 하고, 둘레를
라고 하고, 둘레를
 라고 하면, 원(으로 둘러싸인
圖形
)의
넓이
는
라고 하면, 원(으로 둘러싸인
圖形
)의
넓이
는

이다.
燈住 不等式
에 따르면, 이는 둘레가
 人 닫힌 曲線으로 둘러싸인 圖形이 가질 수 있는 最大 넓이이다.
人 닫힌 曲線으로 둘러싸인 圖形이 가질 수 있는 最大 넓이이다.
方程式
[
編輯
]
데카르트 座標系
[
編輯
]
 中心이
(2, 1)
이고 半지름이 3人 원
中心이
(2, 1)
이고 半지름이 3人 원
2次元
데카르트 座標系
위의 中心이
 이고 半지름이
이고 半지름이
 인 원의 方程式은
인 원의 方程式은

이다.
[1]
:22, §3
이는
피타고라스 整理
를 통해 誘導된다.
2次元 데카르트 座標系 위의 원의 方程式의 一般的인 꼴은

이다. 單,
 는
失手
이며,
는
失手
이며,

이어야 한다.
[1]
:23, §3.2
左邊은 半지름의 4倍에 對應하며, '=0'일 境遇
한元素 集合
이 되고, '<0'일 境遇
空集合
이 된다.
[1]
:24, §3.2, Example 3.2
平面 위의 모든 圓은 適切한 데카르트 座標系를 取했을 때

와 같은 標準的인 方程式으로 表現된다. 單,
 이어야 한다. 이러한 꼴의 方程式을 얻으려면 圓의 中心을 座標系의 原點으로 삼기만 하면 된다.
이어야 한다. 이러한 꼴의 方程式을 얻으려면 圓의 中心을 座標系의 原點으로 삼기만 하면 된다.
2次元 데카르트 座標系 위의 中心이
 이고 半지름이
이고 半지름이
 인 원은 다음과 같은
媒介變數 方程式
을 갖는다.
[1]
:23, §3.2, (3.5)
인 원은 다음과 같은
媒介變數 方程式
을 갖는다.
[1]
:23, §3.2, (3.5)

여기서
 은 各各
코사인 函數
와
사인 函數
이고,
은 各各
코사인 函數
와
사인 函數
이고,
 는 媒介 變數이다.
는 媒介 變數이다.
極座標界
[
編輯
]
데카르트 座標
 代身
極座標
代身
極座標
 를 使用할 수도 있다. 卽,
極座標界
위의 中心이
를 使用할 수도 있다. 卽,
極座標界
위의 中心이
 이고 半지름이
이고 半지름이
 인 원의 方程式은
인 원의 方程式은

이다.
複素平面
[
編輯
]
데카르트 座標나 極座標를
複素數
 로 代身하면, 원과
直線
의 統一된 方程式을 얻을 수 있다.
로 代身하면, 원과
直線
의 統一된 方程式을 얻을 수 있다.
複素平面
위에서, 中心이
 이고 半지름이
이고 半지름이
 인 원의 方程式은
인 원의 方程式은

이다. 여기서
 는 複素數의
絶對값
이다.
는 複素數의
絶對값
이다.
또한 複素平面 위의 원의 方程式의 一般的인 꼴은

이다. 여기서
 는
켤레 複素數
이다. 單,
는
켤레 複素數
이다. 單,
 는
失手
이고,
는
失手
이고,
 는 複素數이며,
는 複素數이며,


이어야 한다. 또한,
 代身
代身
 을 取하고 다른 條件을 그대로 두면 複素平面 위의 直線의 方程式의 一般的인 꼴을 얻는다. 卽,
을 取하고 다른 條件을 그대로 두면 複素平面 위의 直線의 方程式의 一般的인 꼴을 얻는다. 卽,
 이라는 條件을 除去하고 다른 條件을 그대로 두면
一般化 원
의 方程式의 一般的인 꼴을 얻는다.
이라는 條件을 除去하고 다른 條件을 그대로 두면
一般化 원
의 方程式의 一般的인 꼴을 얻는다.
接線의 方程式
[
編輯
]
2次元 데카르트 座標系 위에서, 員

의
 을 接點으로 하는
接線
의 方程式은
을 接點으로 하는
接線
의 方程式은

이다.
원

의 기울기가
 人 接線의 方程式은
人 接線의 方程式은

이다.
幾何적 性質
[
編輯
]
對稱
[
編輯
]
- 원은 지름에 對한
反射
와 圓의 中心에 對한
回戰
에 對하여 對稱이다.
[2]
:227, §20.1, Theorem 20.3
- 卽, 원의
對稱軍
은 2次元
直交群
 이다.
이다.
- 任意의 두 圓은 서로
中心 닮음
이며,
同心圓
이 아닐 境遇 두 圓의 中心을 잇는 線分의 半지름의 비에 따른 內分點 및 外分點을
닮음 中心
으로 갖는다.
[3]
:19, §25
- 半지름의 길이가 같은 모든 圓은 서로
合同
이다.
[4]
:23, §1F
- 공先占
이 아닌 세 點을 지나는 圓은 恒常 唯一하게 存在한다.
[4]
:23, §1F, Theorem 1.15
- 卽, 모든
三角形
의
外接圓
은 唯一하게 存在한다.
- 卽, 任意의 세 點을 지나는
一般化 원
은 恒常 唯一하게 存在한다.
號와 現
[
編輯
]
- 玄의
垂直 二等分線
은 圓의 中心을 지난다.
[2]
:227, §20.1, Theorem 20.2
- 卽, 縣에 垂直인 지름은 弦을 二等分한다.
[2]
:227, §20.1, Theorem 20.2
- 卽, 지름이 아닌 弦을 二等分하는 지름은 縣에 垂直이다.
[2]
:227, §20.1, Theorem 20.2
- 지름은 圓의 가장 긴 縣이다.
[4]
:23, §1F
- (
方冪 整理
) 圓 위에 있지 않은 點
 를 지나는 두 直線 가운데 하나는 圓과 點
를 지나는 두 直線 가운데 하나는 圓과 點
 와
와
 에서 만나고, 다른 하나는 圓과 點
에서 만나고, 다른 하나는 圓과 點
 와
와
 에서 만난다고 하면,
에서 만난다고 하면,
 이다.
[4]
:47, §1H, Theorem 1.35
이다.
[4]
:47, §1H, Theorem 1.35
- 圓 위의 點과 現 사이의 距離와 지름의 곱은 點과 玄의 兩 끝點 사이의 距離의 곱과 같다.
[3]
:71, §101
圓과 直線의 位置 關係
[
編輯
]
平面 위의 圓과 直線의 位置 關係는 圓의 中心에서 直線까지의 距離
 와 圓의 半지름
와 圓의 半지름
 의 對蘇 關係에 따라 다음과 같은 境遇로 나뉜다.
의 對蘇 關係에 따라 다음과 같은 境遇로 나뉜다.
- 萬若
 라면, 圓과 直線은 만나지 않는다.
라면, 圓과 直線은 만나지 않는다.
- 萬若
 라면, 圓과 直線은 한 點에서 만난다. 卽, 直線은 원의
接線
이다.
라면, 圓과 直線은 한 點에서 만난다. 卽, 直線은 원의
接線
이다.
- 萬若
 라면, 圓과 直線은 두 點에서 만난다. 卽, 直線은 원의
割線
이다.
라면, 圓과 直線은 두 點에서 만난다. 卽, 直線은 원의
割線
이다.
두 원의 位置 關係
[
編輯
]
두 원의 位置 關係는 두 圓의 半지름
 와 두 中心 사이의 距離
와 두 中心 사이의 距離
 에 따라 다음과 같은 境遇로 나뉜다.
에 따라 다음과 같은 境遇로 나뉜다.
- 萬若
 이거나
이거나
 라면, 두 圓은 만나지 않는다.
라면, 두 圓은 만나지 않는다.
- 萬若
 라면, 두 圓은 서로의 外部에 놓이며, 交點을 가지지 않는다.
라면, 두 圓은 서로의 外部에 놓이며, 交點을 가지지 않는다.
- 萬若
 라면, 작은 圓은 큰 圓의 內部에 놓이며, 交點을 가지지 않는다.
라면, 작은 圓은 큰 圓의 內部에 놓이며, 交點을 가지지 않는다.
- 萬若
 이거나
이거나
 라면, 두 원은 한 點에서 만난다. 卽, 두 圓은 서로 接한다.
라면, 두 원은 한 點에서 만난다. 卽, 두 圓은 서로 接한다.
- 萬若
 라면, 두 圓은 서로의 外部에서 接한다. 卽, 두 圓은 外接한다.
라면, 두 圓은 서로의 外部에서 接한다. 卽, 두 圓은 外接한다.
- 萬若
 라면, 작은 원이 큰 圓의 內部에서 큰 圓에 接한다. 卽, 두 圓은 內接한다.
라면, 작은 원이 큰 圓의 內部에서 큰 圓에 接한다. 卽, 두 圓은 內接한다.
- 萬若
 라면, 두 원은 두 點에서 만난다.
라면, 두 원은 두 點에서 만난다.
中心角과 圓周角
[
編輯
]
- 주어진 號에 對한
圓周角
의 크기는 그 號에 對한
中心角
의 1/2이다.
[4]
:25, §1F, Theorem 1.16
- 같은 號에 對한 두 圓周角의 크기는 서로 같다.
[4]
:25, §1F
- 켤레弧
에 對한 두 中心角은 서로
보각
이다.
- 卽,
內接 四角形
의 두 大覺은 서로
보각
이다.
[4]
:26, §1F, Corollary 1.17
- 卽, 內接 四角形의 外角의 크기는
內對角
과 같다.
- (
탈레스 整理
) 지름에 對한 圓周角은 直角이다.
- 卽, 三角形의
外心
이 邊 위에 있을 必要充分條件은
直角 三角形
이다.
[4]
:30, §1F, Corollary 1.22
- 圓의 두 玄이 圓 內部에서 이루는 角의 크기는 이 各科
맞꼭지角
의 內部에 包含되는 두 弧에 對한 中心角의 合意 1/2이다.
[4]
:27, §1F, Corollary 1.19
- 圓의 두 할線이 원 外部에서 이루는 角의 크기는 이 角의 內部에 包含되는 두 弧에 對한 中心角의 車의 1/2이다.
[4]
:27, §1F, Corollary 1.18
接線
[
編輯
]
- 圓 위의 한 點을 지나는 圓의 接線은 唯一하게 存在하고, 이는 이 點을 지나는 半지름에 垂直이다.
[2]
:228, §20.1, Theorem 20.4
[4]
:30-31, §1F
- 卽, 半지름의 半지름 끝點에서의 修繕은 圓에 接한다.
[2]
:228, §20.1, Theorem 20.4
- 卽, 圓의 接線의 接點에서의 修繕은 圓의 中心을 지난다.
- 원 外部의 한 點을 지나는 圓의 接線은 正確히 2個이고, 이 點과 두 接點 사이의 距離는 같으며, 두 接線이 이루는 各科 두 接點을 지나는 半지름이 이루는 覺은 서로 補閣이다.
- 원의
椄玄覺
의 크기는 絃을 基準으로 이와 같은 쪽에 있는 號에 對한 中心角의 1/2이다.
[4]
:31, §1F, Theorem 1.23
- 圓의 接線과 할線이 원 外部에서 이루는 覺은 角의 內部에 包含된 두 好意 中心角의 車의 1/2이다.
[4]
:31, §1F, Corollary 1.24
- 外接하는 두 원의 交點을 지나는 두 共通 割線 사이의 두 玄은 서로
平行
한다.
[4]
:31, §1F, Problem 1.25
- (接線에 對한
方冪 整理
)원 外部의 點
 를 지나는 두 直線 가운데 하나는 원과
를 지나는 두 直線 가운데 하나는 원과
 와
와
 에서 만나고, 하나는 원에 點
에서 만나고, 하나는 원에 點
 에서 接한다고 하면,
에서 接한다고 하면,
 이다.
이다.
원의 直交
[
編輯
]
- 두 원의 交點에서의 두 接線이 서로
垂直
일 境遇 두 圓이 서로
直交
한다고 한다.
[3]
:33, §48
- 두 圓의 半지름이
 이고, 두 中心 사이의 距離가
이고, 두 中心 사이의 距離가
 라고 할 때, 두 圓이 서로 直交할 必要充分條件은
라고 할 때, 두 圓이 서로 直交할 必要充分條件은
 이다.
[3]
:34, §48
이다.
[3]
:34, §48
- 주어진 원에 直交하고 中心이 원 外部의 주어진 點인 원은 唯一하게 存在한다.
[3]
:34, §48
- 주어진 원에 直交하고 圓의 지름이 아닌 絃의 두 끝點을 지나는 圓은 唯一하게 存在한다.
[3]
:34, §48
作圖
[
編輯
]
공先占이 아닌 세 點을 지나는 원
[
編輯
]
공先占이 아닌 세 點
 를 지나는 圓은 컴퍼스와 자를 使用하여 다음과 같이
作圖
할 수 있다.
를 지나는 圓은 컴퍼스와 자를 使用하여 다음과 같이
作圖
할 수 있다.
- 線分
 의
垂直 二等分線
을 그린다.
의
垂直 二等分線
을 그린다.
- 線分
 의 垂直 二等分線을 그린다.
의 垂直 二等分線을 그린다.
- 線分
 와
와
 의 交點
의 交點
 를 取한다.
를 取한다.
- 點
 를 中心으로 하고 線分
를 中心으로 하고 線分
 를 半지름으로 하는 圓을 그린다. 이 境遇 원은 點
를 半지름으로 하는 圓을 그린다. 이 境遇 원은 點
 를 지난다.
를 지난다.
圓의 中心
[
編輯
]
주어진 圓의 中心은 컴퍼스와 자를 使用하여 다음과 같이 作圖할 수 있다.
- 圓 위의 두 點
 을 取한다.
을 取한다.
- 線分
 의 點
의 點
 에서의 修繕
에서의 修繕
 를 그린다.
를 그린다.
- 直線
 와 원의 交點
와 원의 交點
 를 取한다. 이 境遇 線分
를 取한다. 이 境遇 線分
 는 圓의 지름이다.
는 圓의 지름이다.
- 또 다른 지름
 을 作圖한다.
을 作圖한다.
- 線分
 와
와
 의 交點
의 交點
 를 取한다. 이 境遇 點
를 取한다. 이 境遇 點
 는 圓의 中心이다.
는 圓의 中心이다.
원적 問題
[
編輯
]
원적 問題
는 주어진 圓과 넓이가 같은 正四角形을 컴퍼스와 字로 作圖하는 問題를 일컫는다. 이는
圓周率
 가
超越數
이므로 不可能하다.
가
超越數
이므로 不可能하다.
其他 關聯 主題
[
編輯
]
內接圓, 外接圓, 傍接圓
[
編輯
]
모든 三角形은 唯一한
內接圓
및
外接圓
과 正確히 3個의
傍接圓
을 갖는다. 그러나, 일一般的로
多角形
은 內接圓이나 外接圓을 가질 必要가 없다. 어떤 多角形이 모든 邊에 接하는 원을 가질 境遇, 이 多角形을
外接 多角形
이라고 한다. 어떤 多角形이 모든 꼭짓點을 지나는 원을 가질 境遇, 이 多角形을
內接 多角形
이라고 한다. 同時에 外接 多角形이며 內接 多角形인 多角形을
二重中心 多角形
이라고 한다. 例를 들어, 모든 三角形과 모든
正多角形
은 이中中心 多角形이다.
주어진 원의 內接
 角形 가운데 넓이가 가장 큰 것은 鄭
角形 가운데 넓이가 가장 큰 것은 鄭
 角形이다.
[4]
:35, §1G
角形이다.
[4]
:35, §1G
文學
[
編輯
]
- 에드윈 A. 애보트의 公傷
數學
小說 《
플랫랜드
》에서는 원이
聖職者
로 出現하며, 平面圖形들 中 가장 高貴한 階級으로 여겨진다.
같이 보기
[
編輯
]
各州
[
編輯
]
- ↑
가
나
다
라
Gibson, C. G. (2003). 《Elementary Euclidean geometry》 (英語). Cambridge: Cambridge University Press.
ISBN
978-0-521-83448-3
.
- ↑
가
나
다
라
마
바
Martin, George E. (1975). 《The Foundations of Geometry and the Non-Euclidean Plane》. Undergraduate Texts in Mathematics (英語). New York, NY: Springer.
doi
:
10.1007/978-1-4612-5725-7
.
ISBN
978-1-4612-5727-1
.
- ↑
가
나
다
라
마
바
Johnson, Roger A. (1960) [1929]. 《Advanced Euclidean Geometry》 (英語). New York, N. Y.: Dover Publications.
- ↑
가
나
다
라
마
바
社
아
者
次
카
타
파
下
거
Isaacs, I. Martin (2001). 《Geometry for College Students》. The Brooks/Cole Series in Advanced Mathematics (英語). Brooks/Cole.
ISBN
0-534-35179-4
.