| この記事は
??可能
な
?考文?や出典
が全く示されていないか、不十分です。
出典を追加
して記事の信?性向上にご協力ください。
(
このテンプレ?トの使い方
)
出典?索
?
:
"円" ??
?
ニュ?ス
·
書籍
·
スカラ?
·
CiNii
·
J-STAGE
·
NDL
·
dlib.jp
·
ジャパンサ?チ
·
TWL
(
2020年9月
)
|

|
この項目では、
??
における
?形
の「円」
について?明しています。
- 日本
の現行
通貨
については「
円 (通貨)
」をご?ください。
- その他の用法については「
円
」をご?ください。
|
??
において、
円
(えん、
英
:
circle
)とは、
平面
(2次元
ユ?クリッド空間
)上の、定点O(オ?) からの距離が等しい
点
の集合でできる
曲線
のことをいう。
その「定点 O(オ?)」を円の
中心
という。円の中心と円周上の 1 点を結ぶ
線分
や、その線分の長さは
半?
という
[1]
[2]
円は
定幅?形
の一つ。
なお円が?む部分すなわち「円の?部」を含めて「円」ということもある。この場合、?密さを必要とする時は、境界となる曲線のほうは「
円周
(circumference)」 という。これに?して、?部を含めていることを?調するときには「
円板
(disk)」 という。また、三角形、四角形などと呼?を統一して「円形」ということもある。
習慣的に、とりあえず円をひとつ?げその中心に名?をつける時は「O (オ?)」と呼ぶことが多い。これは
原点
を英語で「オリジン(
英
:
Origin
)」というのでその
頭文字
をとったものである。中心が点Oである円は「円O(えんオ?)」と呼ぶ。なお中心は英語では「センタ?(
英
:
Center
)」というので、円の中心が「C(シ?)」になっている文?もある
[3]
。
なお、??以外の分野ではこの曲線のことを(あるいはそれに近い
卵形
の??として)「
丸
(まる)」という俗?で呼?することがある。
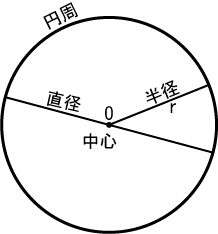 円: 中心、半??直?、円周
円: 中心、半??直?、円周
円の性質
[
編集
]
弦と弧
[
編集
]
円周と2 点で交わる直線を
割線
という。このときの交点を 2 点 A, B とするとき、円周によって、割線から切り取られる線分 AB のことを
弦
といい、弦 AB と呼ぶ。特に円の中心を通る割線を
中心線
という。中心線は円の??軸であり、
円の面積
を 2 等分する。円周が中心線から切り取る弦やその長さを、円の
直?
という。直?は半?の 2 倍に等しい。円周の長さは、円の大きさによってさまざまであるが、円周の長さの直?に?する比の値は、円に依らず一定であり、これを
円周率
という。特に?りのない限り、普通、円周率は
π
で表す。円の半?を
r
(半?の英語 radiusの頭文字が由?) とすると、円周の長さは 2
π
r
で表される。また、
円の面積
は、
π
r
2
で表すことができる。同じ長さの周を持つ閉曲線の中で、面積が最大のものである。(
等周問題
)
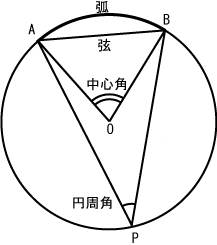 中心角と円周角
中心角と円周角
一方、円周は割線によって 2 つの部分に分けられる。このそれぞれの部分を
円弧
(arc) または?に
弧
という。
- 2つの弧の長さが等しくないとき、長い方の弧を
優弧
(major arc)、短い方の弧を
劣弧
(minor arc) という。
- 2つの弧の長さが等しいとき、これらの弧を
半円周
という。このとき、割線は円の中心を通る中心線である。
円周上の2点 A, B を?端とする弧を弧 AB と呼ぶ。記?では、A?B と表記する(記? ⌒ は AB の上にかぶせて書くのが正しい)。これでは優弧?劣弧のどちらであるかを指定できていないデメリットがあり、一方を特定したい場合は、その弧上の点 P を用いて 弧APB のように表記する。
円 O の周上に2点 A, B があるとき、半? OA, OB と弧 AB とで?まれた?形を
扇形
(sector) O-A?B という。また、扇形に含まれる側の ∠BOA を弧 AB を見?む
中心角
という。一つの円で考えるとき、中心角とその角が見?む弧の長さは
比例
する。同?に、中心角とその角が切り取る扇形の面積も比例する。
弦 AB と弧 AB で?まれた?形を
弓形
(segment) という。
中心角と円周角
[
編集
]
弧 AB に?して、弧 AB 上にない円 O の周上の点 P を取るとき、∠APB を弧 AB に?する
円周角
という。弧 AB に?する円周角は点 P の位置に依らず一定であり、中心角 AOB の半分に等しい(
円周角の定理
)。特に弧 AB が半円周のときは、弧 AB に?する円周角は
直角
である(
直?を見?む円周角
:
タ?レスの定理
)。
 円と?接四角形
円と?接四角形
円 O の周上に 4 点 A, B, C, D があるとき、
四角形
ABCD は円 O に
?接する
という(
?接四角形
)。このとき、円 O を四角形 ABCD の
外接円
という。四角形が円に?接するならば、四角形の?角の和は平角に等しい(
?接四角形の定理
)。円に?接する四角形の外角の大きさは、その
??角
の大きさに等しい。また、これらの逆も成立する(
四点共円定理
、?接四角形の定理)。
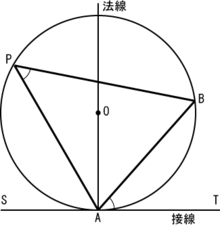 接弦定理
接弦定理
円周と直線が1つの共有点を持つとき、その直線を円の
接線
(tangent) といい、共有点を
接点
という。円の中心と
接点
を結ぶ半?(
接点半?
)は、接線と接点で
直交
する。
円の外部の点 A から円 O に2つの接線が描ける。この接点を S, T とすると、線分 AS, AT の長さを
接線の長さ
という。接線の長さは等しい。円の接線とその接点を通る弦が作る角は、その角の中にある弧に?する円周角に等しい(
接弦定理
)。すなわち、下?で AT が接線ならば、∠BAT = ∠APB である。接弦定理は逆も成立する。
円の
接吻?
は6である。このことの
完全な?明は
1910年
までできなかった。
[
要出典
]
2円の位置?係
[
編集
]
 半?が異なる2円の位置?係
半?が異なる2円の位置?係
位置?係
[
編集
]
2つの円(円 A, 円 B とする)の位置?係は次の場合に分けられる。
- 円 A が円 B の?部にある場合 : 円 B は円 A を
?包する
という。特に、中心の位置が一致するとき、この2円を
同心円
と呼ぶ。
- 円 A が円 B の周または?部にあり、1点のみを共有する場合 : 円 A は円 B に
?接する
という。
- 2円が異なる2点を共有する場合 : 2円は2点で
交わる
という。この2点を結ぶ弦を
共通弦
という。
- 2円が互いの周または外部にあり、1点のみを共有する場合 : 円 A は円 B に
外接する
という。
- 2円が互いの外部にあり、共有点がない場合 : 2円は
離れている
という。
共通弦の性質
[
編集
]
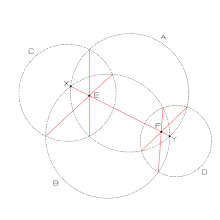 直線XYを共通弦とする正円をA?B、Xを包みYを外にする正円をC、Yを包みXを外にする正円をD、ACの共通弦とBCの共通弦の交点をE、ADの共通弦とBDの共通弦の交点をF、とした時、EとFはXYの線上にある。
直線XYを共通弦とする正円をA?B、Xを包みYを外にする正円をC、Yを包みXを外にする正円をD、ACの共通弦とBCの共通弦の交点をE、ADの共通弦とBDの共通弦の交点をF、とした時、EとFはXYの線上にある。
 三角形の三?の位置と長さそのものを
直?
とする三つの円によって生じる3本の共通弦は、その三角形の3本の
頂垂線
となる。
三角形の三?の位置と長さそのものを
直?
とする三つの円によって生じる3本の共通弦は、その三角形の3本の
頂垂線
となる。
- ?定の共通弦を持つ2円(A?B)と、その共通弦の一端のみを包む任意の別の円Cとの間にできる2本の共通弦(ACとBCの共通弦)の交点は、ABの共通弦上に存在する。
- 三角形の三?の位置と長さそのものを
直?
とする三つの円によって生じる3本の共通弦は、その三角形の3本の
頂垂線
となる。
共通接線
[
編集
]
2つの円に共通する
接線
を
共通接線
という。
特に、2円が共通接線に?して、同じ側にあるとき
共通外接線
、異なる側にあるとき
共通?接線
という。
上記の場合分けにおいて、描ける共通接線の個?は、
- なし
- 共通外接線1本
- 共通外接線2本
- 共通?接線1本、共通外接線2本の計3本
- 共通?接線2本、共通外接線2本の計4本
のいずれか。
円の方程式
[
編集
]
 半?
r
? 1
, 中心
(
a
,
b
) ? (1.2, ?0.5)
の円
半?
r
? 1
, 中心
(
a
,
b
) ? (1.2, ?0.5)
の円
解析幾何?
において、
(
a
,
b
)
を中心とする半?
r
の円は

を?たす点
(
x
,
y
)
全?の
軌跡
である。この方程式を、
円の方程式
と言う。これは、中心
(
a
,
b
)
と円上の任意の点
(
x
,
y
)
との二点間の距離が
r
であるということを述べたものに他ならず、半?を斜?とする直角三角形に
ピタゴラスの定理
を適用しすることで導出できる(直角を?む二?は、各座標の
絶?差
|
x − a
|, |
y − b
|
を長さとする)。
- 中心を原点に取れば、方程式は
 と簡?になる。
と簡?になる。
α, β, γ, δ
は??で
α
≠ 0
なるものとし、

と書けば、上記の方程式は

の形になる。この形(
x
2
,
y
2
の係?が等しく、
xy
の項を持たない)の方程式が?えられたとき、以下の何れか一つのみが成り立つ:
- ρ
< 0
のときは、この方程式に解となる?点は存在しない。この場合を
?円
[4]
(
imaginary circle
) の方程式と呼ぶ。
- ρ
= 0
のとき、方程式
f
(
x
,
y
) = 0
は中心となる一点
O
? (
a
,
b
)
のみを解とし、
点円
[5]
(
point circle
) の方程式と言う。
- ρ
> 0
のときには、
f
(
x
,
y
) = 0
は
O
を中心とする半?
r
?
√
ρ
の円(あるいは
?円
(
real circle
))の方程式になる。
α
= 0
のとき
f
(
x
,
y
) = 0
は直線の方程式であり、
a, b, ρ
は(射影平面上で、あるいは見かけ上)無限大になる。?は、直線を「
無限遠点
を中心とする半?無限大の円」と考えることができる(
一般化された円
(
英語版
)
の項を?照)。
別の表示法
[
編集
]
- ベクトル表示
- 中心の位置ベクトルを
c
とし、円上の任意の点の位置ベクトルを
x
とすると、これら二点間の距離は、ベクトルの
ユ?クリッドノルム
‖ • ‖ ? ‖ • ‖
2
: (
x
,
y
) ?
√
x
2
+
y
2
を用いて、
‖
x
−
c
‖
と書けるから、半?
r
の円の方程式は

 は上記の円の方程式である。
は上記の円の方程式である。
- 媒介??表示
- (
a
,
b
)
を中心とする半?
r
の円の方程式を
正弦函?
および
余弦函?
を用いて

- 円の別の媒介表示が
半角正接置換
により、

その他の標準形
[
編集
]
- 三点標準形
- 同一直線上
にない三点を
(
x
i
,
y
i
)
(
i
= 1, 2, 3
) とすると、その三点を通るという?件を?たす円は一つに決まり、その方程式を


射影平面
[
編集
]
射影平面
上の円の方程式は、円上の任意の点の
?次座標
(
英語版
)
を(
埋め?み
(
x
,
y
) ? [
x
:
y
: 1]
のもとで)
[
x
:
y
:
z
]
と書くとき、その一般形を

と書くことができる。
極座標系
[
編集
]
平面の座標系として、
直交座標系
の代わりに
極座標系
を用いれば、円の方程式の極座標表示が作れる。円上の任意の点の極座標を
(
r
,
θ
)
とし、中心の極座標を
(
r
0
,
φ
)
(つまり、中心の原点からの距離が
r
0
で、
φ
は原点から中心へ結んだ半直線が、
x
-軸の正の部分から反時計回りになす角)とするとき、半?
ρ
の
円の極方程式
は

と書ける。
- 中心が原点にあるときには、方程式は
r
=
ρ
(
θ
は任意) という?純な形をしている(極座標系において原点は、動?成分が
r
= 0
かつ偏角成分
θ
は任意と表されるのであった)。
- 原点が円上にあるとき、方程式は
 と簡約される。例えば、半?
ρ
が中心の動?成分
r
0
に等しいときはそうである。
と簡約される。例えば、半?
ρ
が中心の動?成分
r
0
に等しいときはそうである。
- 一般の場合の方程式を
r
について解くことができて、

複素?平面
[
編集
]
複素?平面
を用いれば、平面上の円は複素?を用いても記述できる。中心が
c
で半?が
r
の円の方程式は、
複素?の絶?値
を用いて

と書ける。これは本質的に
円のベクトル方程式
と同じものである(複素?平面における複素?の加法および??倍は、成分表示された平面ベクトルの加法および??倍と同一であり、複素?の絶?値はユ?クリッドノルムと同一視できる)。
極形式
を考えれば、
|
z − c
| =
r
という?件は、
z − c
=
r
⋅
exp
(
iθ
)
(
θ
は任意) と同値であることがわかる(これは上記の
媒介??表示
に??する)。
複素?の積に?して
|
z
|
2
=
z
⋅
z
が成り立つことに注意すれば、この方程式は??
p, q
および複素?
g
を用いて

の形に書ける(

)。この形の方程式は、円だけでなく一般には
一般化された円
(
英語版
)
を表すものである(一般化された円とは、通常の円となるか、さもなくば
直線
である)。
極方程式
も
極形式
を用いれば複素?で記述できる。
接線の方程式
[
編集
]
円上の点
P
における
接線
は、
P
を通る直?に垂直である。したがって、円の中心を
(
a
,
b
)
, 半?を
r
とし、
P
? (
x
1
,
y
1
)
とすれば、垂直?件により接線の方程式は
(
x
1
?
a
)
x
+ (
y
1
?
b
)
y
=
c
の形をしていなければならない。これが
(
x
1
,
y
1
)
を通るから
c
は決定できて、接線の方程式は

または

の形に書ける。
y
1
≠
b
ならばこの接線の傾きは

であるが、これを
陰函?微分法
を用いて求めることもできる。
中心が原点にあるときは、接線の方程式は
 となり、傾きは
となり、傾きは
 である。原点を中心とする円では、各点の位置ベクトル
(
x
,
y
)
と接ベクトル
(
dx
,
dy
)
が常に
直交
する(つまり、?積が零になる)から、
である。原点を中心とする円では、各点の位置ベクトル
(
x
,
y
)
と接ベクトル
(
dx
,
dy
)
が常に
直交
する(つまり、?積が零になる)から、
 は微分形の円の方程式である。
は微分形の円の方程式である。
円の幾何?
[
編集
]
三角形
や円に?する事柄を扱う
幾何?
(相似や面積を用いない)は
円論
と呼ばれ、古?非常に深く?究されてきた。最も
平面幾何?
らしい幾何?とも呼ばれる。
九点円の定理
[
編集
]
三角形の
- それぞれの頂点から??に下ろした垂線の足(3つ)
- ?の中点(3つ)
- 頂点と垂心を結んだ線分の中点(3つ)
は全て同一円上にある。この円のことを九点円と呼ぶ。
六点円の定理
[
編集
]
三角形のそれぞれの頂点から下ろした垂線の足から他の二?に下ろした、合計 6 個の垂線の足は、同一円周上にある、という定理。中?で習う円の性質だけで?明することができるが、かなり難解。
パスカルの定理
[
編集
]
円に?接する六角形の??の延長線の交点は一直線上にある。さらに?張して、二次曲線上に異なる6つの点 P
1
~P
6
を取ると、直線 P
1
P
2
と P
4
P
5
の交点 Q
1
、P
2
P
3
と P
5
P
6
の交点 Q
2
、P
3
P
4
と P
6
P
1
の交点 Q
3
は同一直線上にある。また、P
i
における接線と P
j
における接線の交点を R
ij
とすると、3 直線 R
12
R
45
, R
23
R
56
, R
34
R
61
は1点で交わる。一番初めの、円に?接する六角形の?明は、うまく補助円を書くことで、円の性質と三角形の相似だけですることができる。
フォイエルバッハの定理
[
編集
]
三角形の
?接円
は、九点円に?接する。
一般化
[
編集
]
球面?超球面
[
編集
]
3 次元ユ?クリッド空間においてある点からの距離が一定であるような点の集合を球面という。?部を含めた球面を
球
という。一般に、
n
を自然?とするとき、
n
+ 1 次元ユ?クリッド空間においてある点からの距離が一定であるような点の集合のことを、
n
次元球面といい、
S
n
と書く。円は 1 次元球面である。
円錐曲線
[
編集
]
2つの点(焦点と呼ばれる)からの距離の和が一定であるような点の軌跡を
楕円
という。楕円は一般に円を潰したような形をしており、楕円のうち特別な場合――2つの焦点が一点で一致する場合――が円である(このとき、焦点は「円の中心」と呼ばれる)。一般の楕円でなく円であることを特に明示したいときには、円のことを
正円
(せいえん)または
?円
(しんえん)と呼ぶことがある。
距離円、ノルム円
[
編集
]
 異なる
p
に?する
p
-ノルム
?位円
を?示したもの。
異なる
p
に?する
p
-ノルム
?位円
を?示したもの。
「定点からの距離が一定である点全?の成す集合」として円を定義するならば、定義に用いる「距離」の定義を?えれば異なる形?の「円」を考えることができるということになる。
p
-ノルム
(
英語版
)
の誘導する距離は

で?えられる。ユ?クリッド幾何?における通常の
ユ?クリッド距離
:

は
p
= 2
の場合である。
タクシ?幾何?で用いる
マンハッタン距離
(
L
1
-距離)は
p
= 1
の場合であり、この距離に?する円(タクシ?円)は各?が座標軸から
45°
ずれた
正方形
となる。半?
r
のタクシ?円の各?の長さは、ユ?クリッド距離で測れば
√
2
r
だが、タクシ?距離で測れば
2
r
である。よって、この幾何?で
円周率
(半?に?する周長の比)に相?するものは
4
ということになる。タクシ?幾何?における?位円(半?が 1 の円)の方程式は、
直交座標系
では
 ,
極座標系
では
,
極座標系
では
 と書ける。これは、その中心の
フォンノイマン近傍
(
英語版
)
である。
と書ける。これは、その中心の
フォンノイマン近傍
(
英語版
)
である。
平面上の
チェビシェフ距離
(
L
∞
-距離)に?する半?
r
の円もまた各?の長さが
2
r
の正方形(ただし、各?は座標軸に平行)であるから、平面チェビシェフ距離は平面マンハッタン距離を回?およびスケ?ル?換したものと看做せる。しかし
L
1
と
L
∞
の間に成り立つこの同値性は他の次元に一般化することはできない。
その他の円を特別の場合として含む曲線族
[
編集
]
円は他の??な?形の極限の場合と見ることができる:
- デカルトの卵形線は
焦点
と呼ばれるふたつの定点からの距離の重み付き和が一定となるような点全?の成す軌跡である。各距離に付ける重みが全て等しいとき
楕円
となり、
離心率
が
0
であるような楕円として円が得られる(これは二つの焦点が互いに重なる極限の場合であり、一致した焦点は得られる円の中心となる)。ふたつの重みのうちの一方を
0
として得られるデカルトの卵形線としても、円が得られる。
- 超楕円
は、適?な正?
a, b > 0
と自然?
n
に?する
 の形の方程式を持つ。
b
=
a
のとき超円と言う。円は
n
= 2
となる特別な超円である。
の形の方程式を持つ。
b
=
a
のとき超円と言う。円は
n
= 2
となる特別な超円である。
- カッシ?ニの卵形線
は二つの定点からの距離の積が一定となるような点全?の軌跡を言う。ふたつの定点が一致するとき、円が得られる。
- 定幅曲線
は、その幅—?形の幅は、それを?む二つの平行線が、各?その?形の境界と一点のみを共有するときの、それら平行線間の距離として定める—が平行線の方向のとり方に依らず一定であるような?形を言う。円はもっとも?純な定幅曲線形の例である。
?幅円弧の長さ
[
編集
]
半?
R
の円弧上の始点で幅
w
1
、終点で幅
w
2
の?幅円弧の長さの計算


とすると、


ゆえに、?幅円の長さは、平均半?に中心角をかけたものとなる。
脚注
[
編集
]
出典
[
編集
]
?考文?
[
編集
]
?連項目
[
編集
]
ウィキメディア?コモンズには、
円 (??)
に?連する
メディア
および
カテゴリ
があります。
特別な名?のある円
[
編集
]
三角形に?する円
[
編集
]
四?形に?する円
[
編集
]
多角形に?する円
[
編集
]
円錐曲線に?する円
[
編集
]
球面に?する円
[
編集
]
ト?ラスに?する円
[
編集
]
外部リンク
[
編集
]