
3.1415926535897932384626433832795……
|
圓周率
(圓周率,
文化語
:
原州率)은
圓둘레
와 지름의 비 卽,
원
의
지름
에 對한
둘레
의
比率
을 나타내는
數學 常數
이다.
數學
과
物理學
의 여러 分野에 두루 쓰인다.
그리스 文字
π
로 表記하고,
파이
(π)라고 읽는다.
[1]
圓周率은 數學에서 다루는 가장 重要한 上水 가운데 하나이다.
[2]
無理手
人 同時에
超越數
이다.
아르키메데스
의 計算이 널리 알려져 있어
아르키메데스 常數
라고 부르기도 하며, 獨逸에서는 1600年代
뤼돌프 판 쾰런
이 小數點 以下 35자리까지 圓周率을 計算한 以後
뤼돌프 수
라고 부르기도 한다.
[3]
圓周率의 값은 循環하지 않는 無限小數(
無理手
)이기 때문에, 圓周率을 包含한 計算에서는 3.14 또는 3.141 等 첫 小數點 아랫자리를 醉한 近似값을 使用하거나 記號 파이(
π
)를 使用한다.
槪要
[
編輯
]
 圓의 지름이 1일 때, 원주는 π이다.
圓의 지름이 1일 때, 원주는 π이다.
유클리드 平面
에서
원
은 크기와 關係없이 언제나
닮은 圖形
이다. 따라서 원의
지름
에 對한
둘레
의
비
는 언제나 일정하며, 이를 圓周率이라 한다. 卽, 圓의 지름을 d, 둘레를 C라 하면 圓周率 π는 다음의 式으로 나타낼 수 있다.
[4]

圓周率을 나타내는 記號 π는 1706年 英國의 數學者
윌리엄 존스
賈 最初로 使用했다. 이것은 둘레를 뜻하는
古代 그리스어
"페리페레스"(περιφηρ??) 또는 "페리메트론"(περ?μετρον)의 첫 글字를 딴 것이다.
[5]
윌리엄 존스는 “特定 圖形의 길이나 넓이를 求하는 計算에 매우 有用한 方法이 여러 가지 있다. 원을 例로 들면 지름이 1인 圓의 둘레를 約 3.14159…= π로 表記하는 것이다.”라고 記號 π의 使用을 提案하였다.
[6]
圓周率은 小數點 아래 어느 자리에서도 끝나지 않고,
循環마디
도 없이 無限히 繼續되는
비
循環小數
이다. 圓周率이
無理手
라는 것은
1761年
요한 하인리히 람베르트
가 證明했다. 圓周率의 小數點 以下에서 나타나는 數列은 無作爲
標集
을 통해 만드는 亂數表와 性質이 같다.
[7]
圓周率은
十進法
으로는 값을 正確하게 表記할 수 없기 때문에 實際 計算에서는
近似값
을 利用한다.
 圓의 넓이 = π × 半지름
2
圓의 넓이 = π × 半지름
2
 圓의 둘레 = π × 지름
圓의 둘레 = π × 지름
 圓積問題
圓積問題
 다빈치의 圓의 넓이 計算
다빈치의 圓의 넓이 計算
한便, 圓周率은 係數가
有理數
人 有限 次數
多項式
의 해가 될 수 없다. 이러한 種類의 數를
超越數
라 부른다. 이 事實은
1882年
페르디난트 폰 린데만
이 證明하였다. 여기에서 圓周率은 어떤
精髓
에 適當한 有理數를 곱하고
제곱根
을 씌우는 等의
演算
을 組合하여 얻어낼 수 없다는 事實을 알 수 있다. 또한 圓周率이 超越數라는 事實을 통해,
그리스
3大 難題 中 하나였던 “
者
와
컴퍼스
만을 使用하여
원
과 넓이가 같은
正四角形
을
作圖
하는
圓積問題
”가 有限한 代數的 方法으로는 不可能하다는 것을 證明할 수 있다.
유클리드 幾何學
에서 원과 圓周率의 關係를 살펴보면 다음과 같은 事實을 確認할 수 있다.
[8]
:183
- 圓의 둘레를 求하는 式은 圓周率의 定義와 같다.
- 圓의 둘레 = 지름 × 圓周率
- 圓의 넓이를 求하는 方法은 아르키메데스 時代 以後 여러 가지 技法이 알려져 있다. 널리 使用하는 方法 가운데 하나는
레오나르도 다빈치
가 考案한 것으로,
正六角形
을 利用한 求積法이다. 레오나르도 다빈치는 왼쪽 그림과 같이 正六角形을 利用하여 分割한 원을 直四角形으로 置換하여 圓의 넓이를 計算하였다.
[9]
- 圓의 넓이 = 圓周率 × 半지름
2
圓周率이 보이는 複雜한 數列에 비해 이를 計算하는 方法은 意外로 單純하다.
라이프니츠
가 整理한 다음 計算食餌 널리 알려져 있다.

歷史
[
編輯
]
古代
[
編輯
]
古代의 여러 文化에서 圓周率의 값으로
3
이 쓰였다. 古代
메소포타미아
에서도 圓周率을 3으로 計算하였고
[10]
,
舊約聖經
列王記上 7張 23節과 歷代下 4張 2節에는 直徑과 둘레의 길이를 記述하여 圓周率이 3程度 임을 알고 있었다고 推測된다.
古代 中國
의 數學冊人 《
九章算術
》에서도 3을 圓周率로 提示하였다. 《九章算術》에는 다음과 같은 問題가 실려 있다.
[11]
| 原文
|
飜譯
|
今有圓田周三十步經十步問爲田幾何
答曰七十五步
|
둘레가 30걸음, 지름이 10걸음인 圓 模樣의 밭이 있다면 넓이는 얼마인가?
答: 75걸음²
|
圓周率의 近似값을 3.14로 할 때 오늘날의 計算은

|
九章算術의 計算은 平均값으로 이루어져있다. (1) 圓둘레가 30보인 境遇 半지름은 30=2r*3.14 r=4.78 이경우의 面積은 71.74 (2) 지름이 10보인 境遇 面積은 78.5. (1)과 (2)의 平均은 75報. 그러므로 九章算術의 計算이 不正確하다는 것은 잘못되었다.
 圓에 內接하는 正六角形
圓에 內接하는 正六角形
九章算術에 실린 計算이 매우 不正確하다는 것은 왼쪽 그림을 보면 쉽게 알 수 있다. 지름이 1인 圓에 內接하는 正六角形의 둘레는 3이고 實際 圓의 둘레는 그것과는 差異가 相當하기 때문이다.
[12]
이는
古代
에서부터 이미 널리 알려진 問題였고 값을 보다 正確하게 求하기 위한 努力이 繼續되었다.
古代 이집트
에서는 圓筒形 바퀴를 굴려 直接 測定해 圓周率을 計算하였는데
256
⁄
81
=3.16049……를 使用하였다.
[10]
 圓에 外接하는 多角形과 內接하는 多角形의 둘레를 利用한 아르키메데스의 圓周率 計算
圓에 外接하는 多角形과 內接하는 多角形의 둘레를 利用한 아르키메데스의 圓周率 計算
한便 紀元前 3世紀의
古代 그리스
數學者
아르키메데스
는 近代
積分
이 없었던 當時에
無限小
라는 槪念을 使用하였다. 그는
消去法
을 使用하여
 의
近似값
을 計算하였다. 이 方法은 임의 次元의 未知項에 對해
極限
을 取하는 것으로,
歸謬法
을 使用하여 同一한 計算을 反復하는 過程을 통해 解答을 얻는 것이다. 아르키메데스는 變異 매우 많은
多角形
이 任意의
원
에 內接하는 境遇와 外接하는 境遇를 比較하여 圓周率을 計算하였다. 卽, 任意의 圓의 둘레는 그것에 外接하는 多角形의 둘레보다 짧고 內接하는 多角形보다 길다. 이때 多角形의 變異 많아질수록 外接하는 境遇와 內接하는 境遇의 둘레 車는 작아지므로 圓의 둘레에 近似한다. 卽, 지름이 d인 圓에 內接하는 邊의 個數가 n인
正多角形
의 둘레 P
n
에 對해 다음과 같이
函數의 極限
을 取하면 圓周率을 얻을 수 있다.
의
近似값
을 計算하였다. 이 方法은 임의 次元의 未知項에 對해
極限
을 取하는 것으로,
歸謬法
을 使用하여 同一한 計算을 反復하는 過程을 통해 解答을 얻는 것이다. 아르키메데스는 變異 매우 많은
多角形
이 任意의
원
에 內接하는 境遇와 外接하는 境遇를 比較하여 圓周率을 計算하였다. 卽, 任意의 圓의 둘레는 그것에 外接하는 多角形의 둘레보다 짧고 內接하는 多角形보다 길다. 이때 多角形의 變異 많아질수록 外接하는 境遇와 內接하는 境遇의 둘레 車는 작아지므로 圓의 둘레에 近似한다. 卽, 지름이 d인 圓에 內接하는 邊의 個數가 n인
正多角形
의 둘레 P
n
에 對해 다음과 같이
函數의 極限
을 取하면 圓周率을 얻을 수 있다.

아르키메데스는 正九十六角形을 利用하여
 의 값을 다음과 같이 計算하였다.
[13]
의 값을 다음과 같이 計算하였다.
[13]

아르키메데스는 이 結果에 따라
 의 近似값으로 3.1416을 提示하였다. 또한, 아르키메데스는 圓의 面積이
의 近似값으로 3.1416을 提示하였다. 또한, 아르키메데스는 圓의 面積이
 임을 證明하였다. 아르키메데스는 自身의 著書 《球와 圓기둥》에서 어떠한 크기가 주어지더라도 任意의 크기에 適當한 數를 곱하여 주어진 크기를 超過할 수 있다고 假定하였다. 이를
失手
에서의
아르키메데스 性質
이라고 한다.
[14]
임을 證明하였다. 아르키메데스는 自身의 著書 《球와 圓기둥》에서 어떠한 크기가 주어지더라도 任意의 크기에 適當한 數를 곱하여 주어진 크기를 超過할 수 있다고 假定하였다. 이를
失手
에서의
아르키메데스 性質
이라고 한다.
[14]
中國의
三國時代
위나라
數學者
劉徽
는 《九章算術》에 註解를 달아 다시 出版하였는데, 아르키메데스와 같은 方法을 使用하여 圓周率을
157
⁄
50
=3.14 로 計算하였다. 劉徽가 計算한 圓周率 近似값은 오늘날에도 日常生活에서 使用한다.
[15]
2世紀에 들어 中國의 張型은 圓周率을 3.1623으로 計算하였고
[16]
5世紀 中國
南北朝 時代
宋나라
의
祖冲之
는 3.141592로 計算하였다.
[17]
獨逸에서는 1600年代
뤼돌프 판 쾰런
이 小數點 以下 35자리까지 計算하였다.
[3]
컴퓨터를 導入하기 以前에 가장 긴 자리數의 圓周率을 計算한 사람은 英國의 數學者 샹크스였다. 그는 15年이나 걸려 1873年까지 小數點 以下 707자리까지 圓周率 값을 計算해냈다. 하지만 後에 그 計算은 528자리까지만 正確한 것으로 밝혀졌다.
[18]
컴퓨터를 통한 圓周率 計算
[
編輯
]
1949年
9月 最初로
컴퓨터
를 利用하여 70時間에 걸쳐 小數點 아래 2,037자리까지 計算하였다. 圓周率 計算에 컴퓨터를 導入한 以後 圓周率 計算은 單純
알고리즘
의 無限 反復에 不過한 作業이 되어 數學的 意味를 잃었다.
[19]
이 計算은 種種 컴퓨터의 性能을 試驗하기 위한 方法으로 使用한다.
[18]
2005年 日本
도쿄 大學
의 가네다 야스마사 敎授는 컴퓨터를 601時間 56分 동안 使用하여 圓周率을 小數點 1,241,100,000,000자리까지 求하였다. 2009年 〈도쿄신문〉에 따르면, 日本
쓰쿠바 大學
計算科學硏究센터는 17日, 슈퍼컴퓨터를 使用한 圓周率 計算에서, 2兆 5769億 8037萬 자리數의 世界記錄을 樹立했다고 한다. (73時間 59分 所要)
[20]
[21]
그 以後 프랑스에서는 2兆 7千億 자리까지 計算하였다.
[22]
2010年 8月 3日에는 日本의 會社員 곤도 시게루(近藤茂)가 小數點 以下 5兆 자리까지 計算하였다. (90日 7時間 所要, 檢證 期間 包含 / PC 使用)
[23]
2016年 11月 11日 스위스의 粒子 物理學者인 페터 트뤼프(Peter Trub)는 105日 동안 計算하여, 圓周率을 小數點 以下 22兆 4591億 5771萬 8361자리(
 兆 個)까지 計算했다.
[24]
兆 個)까지 計算했다.
[24]
圓周率의 값
[
編輯
]
 값의 小數點 아래 1,000자리 數는 다음과 같다.
값의 小數點 아래 1,000자리 數는 다음과 같다.
3.1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679
8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196
4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273
7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094
3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912
9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132
0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235
4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859
5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303
5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989...
數學的 特性
[
編輯
]
圓周率은 두
精髓
의 比로 나타낼 수 없는
無理手
이다. 또한,
計數
가
有理數
人
多項式
의
近
이 될 수 없는
超越數
이다.
無理手
[
編輯
]
圓周率이
無理手
라는 것은 1761年에
요한 하인리히 람베르트
가 證明했다.
[25]
람베르트는 다음과 같이
탄젠트
函數의
連分數
展開式을 利用하여 이를 證明하였다.
[26]

 가
가
 이 아닌
有理數
일 때 위에 展開된 連分數를 十進記數法으로 나타내면 언제나 循環하지 않는 少數이므로 恒常 無理數이다. 한便,
이 아닌
有理數
일 때 위에 展開된 連分數를 十進記數法으로 나타내면 언제나 循環하지 않는 少數이므로 恒常 無理數이다. 한便,
 이므로
이므로
 는 반드시 無理手餘萬 한다. 따라서
는 반드시 無理手餘萬 한다. 따라서
 亦是 無理數이다.
[27]
[註解 1]
亦是 無理數이다.
[27]
[註解 1]
超越數
[
編輯
]

오일러 等式
은 基礎 數學의 여러 槪念에서 頻繁하게 登場한다.
圓周率이
超越數
임은
오일러 等式
을 利用하여 다음과 같이 證明할 수 있다.
[28]
오일러 等式은,
 …… (1)
[註解 2]
…… (1)
[註解 2]
이다. 이 때 π가 정계수 代數方程式
 의 근이라면
의 근이라면
 이다. 따라서
이다. 따라서
 亦是 成立夏여야 한다. 이제 y=iπ라 하면 π=-iy 이고 -π=iy 이므로, iπ는 다음 式으로 나타낼 수 있는 정계수 代數方程式을 만족시켜야 한다.
亦是 成立夏여야 한다. 이제 y=iπ라 하면 π=-iy 이고 -π=iy 이므로, iπ는 다음 式으로 나타낼 수 있는 정계수 代數方程式을 만족시켜야 한다.

이제
 을 ν次元의 方程式이라 하면 그
近
人 y
1
, y
2
,……, y
ν
에는 iπ가 存在하여야 하므로, 式 (1)에 따라 다음과 같이 나타낼 수 있다.
을 ν次元의 方程式이라 하면 그
近
人 y
1
, y
2
,……, y
ν
에는 iπ가 存在하여야 하므로, 式 (1)에 따라 다음과 같이 나타낼 수 있다.

그런데 이러한 關係를 滿足하는 代數方程式의 根이 有理數라고 假定하면 無限히 約分할 수 있어서, 이를 旣約分數로 表現할 수 없는 矛盾이 생긴다.
[註解 3]
有理數를 旣約分數로 表現할 수 없다는 것은 有理數의 正義에 어긋나므로 π가 정계수 代數方程式
 의 斤이라는 最初의 家庭이 잘못되었다고 볼 수밖에 없다. 卽, 圓周率은 超越數이다. 仔細한 證明은 링크한 註釋을 參考하기 바란다.
[29]
의 斤이라는 最初의 家庭이 잘못되었다고 볼 수밖에 없다. 卽, 圓周率은 超越數이다. 仔細한 證明은 링크한 註釋을 參考하기 바란다.
[29]
水熱
[
編輯
]
槪要에서 밝혔듯이 圓周率은 反復되지 않고 無限히 繼續되는 數列을 이룬다.
네덜란드
數學者
라위트展 브라우어르
는 다음과 같은 質問을 提起하였다.
[30]
- 圓周率 π = 3.141592……醫 展開에서 繼續되는 少數의 數列에 9街 連續的으로 100回 나타날까?
브라우어르는 이 數列이 無限히 繼續되기 때문에 이 數列을 어느 程度까지만 確認한 結果만으로는 위 質問에 答할 수 없다는 點을 指摘하였다. 實際 小數點 以下 762番째에서부터 水熱 999999 가 出現한다. 이 數列은
파인만 포인트
로 알려져 있으며 圓周率의 小數點 以下 數列에서 確率 0.08%로 發見할 수 있는 것으로 알려져 있다.
[31]
따라서 經驗的 方法으로는 위 問題에 答할 수 없다. 브라우어르는 이러한 論議를 바탕으로
아리스토텔레스
의 排中律
[註解 4]
은 有限한 個數를 對象으로 한 것에만 適用 수 있을 뿐 無限한 것에 適用할 수 없다고 結論지었다.
[30]
圓周率에서 나타나는 數列은 無作爲
標集
을 使用해 만든 亂數表의 性質을 보인다. 하지만, 實際 圓周率의 數列이 完全한 無作爲性을 보이는지는 證明되지 않았다.
[7]
計算式
[
編輯
]
圓周率은
無理手
利器 때문에 그 값은 近似값으로밖에 알 수 없다. 大部分의 計算에는 3.14나 22/7 라는 近似값을 使用해도 充分하다. 355/113은 외우기 좋고, 精密度도 좋다. 좀 더 精密한 技術의 計算에서는 3.1416 또는 3.14159 等을 使用하기도 한다. 氣象 豫報나 人工 衛星 等의 計算에는 小數點 아래 30자리까지 나아간 近似값을 使用하고 있다. 이렇게 不規則的인 패턴을 가지는 圓周率은 다음과 같이 規則的인 修飾을 利用하여 計算할 수 있다. 더 正確한 값을 얻으려면 修飾을 延長하기만 하면 된다.
[19]

위 식은
고트프리트 빌헬름 라이프니츠
가 展開한 것으로 흔히
라이프니츠의 公式
이라고 부른다. 이 式 外에도 圓周率을 計算하는 公式으로는 다음과 같은 것이 있다.
[32]
 ……
월리스 公式
1655年
……
월리스 公式
1655年
 ……
오일러의 곱셈 公式
1735年
[註解 5]
……
오일러의 곱셈 公式
1735年
[註解 5]
17世紀
의 프랑스 數學者
프랑수아 비에트
는 다음과 같은 無限級數로 圓周率을 計算하였다.
[33]
[34]

또한,
스털링 近似
를 使用해 圓周率을 誘導할 수도 있다.
[35]

圓周率은 다음과 같이
連分數
로 表現할 수 있다.
[36]

1996年
데이빗 베일리는 피터 補語와인, 시몽 플루프와 共同으로 π에 關聯된 새로운 無限級數를 發見했다.

이 式을 利用하면
2眞數
그리고
16眞數
로 表記한 π값의 小數點 아래
n
자리 값을
n
-1째 자리까지 求하지 않고 바로 計算해 낼 수 있다.
베일리의 홈페이지
에선 다양한
프로그래밍 言語
를 利用해 具現한 實際 例를 볼 수 있다.
適用
[
編輯
]
圓周率은
數學
과
物理學
等 여러 分野에서 다양하게 適用한다.
幾何學
[
編輯
]
아르키메데스
는
원
과
區
의 다음과 같은 性質을 證明하였다.
[37]
- 半지름
r
인 원의
둘레
:

- 半지름
r
인 원의
넓이
:

- 半지름
r
人 區의
부피
:

- 半지름
r
人 區의
겉넓이
:

한便, 원은
離心率
이 0人
楕圓
으로 看做할 수 있으며 이에 따라 楕圓 方程式은 一般的으로 다음과 같이 表現한다.
[38]
:70

이 때 楕圓의 넓이를 A라 하면 다음과 같이 計算할 수 있다.

 라디안의 正義
라디안의 正義
角의 크기를 나타내는 無次元 單位인
라디안
은 오른쪽 그림과 같이 定義하여 半지름과
號
의 길이가 같을 때 1라디안이 된다. 따라서, 圓 全體는 2π라디안이고 이를
도
로 換算하면 다음과 같다.
[38]
:119
바젤 問題
[
編輯
]
1687年
스위스
의
바젤
의 數學 敎授였던
야코프 베르누이
와
요한 베르누이
兄弟는
調和級數
가
發散
한다는 事實을 證明하였다. 그러나, 調和級數의 各 分母를 제곱한 다음 式을 닫힌 形式으로 나타내는 것에는 失敗하였으며 論文의 끝에 이 問題를 解決하였다면 알려주기 바란다고 적었다.

當代의 有名한 數學者들이 이 問題를 풀기 위해 試圖하였으나 結局 失敗하였고, 이 問題는
바젤 問題
로 알려지며
解釋學者
의 惡夢으로까지 불리게 되었다. 이를 解決한 사람은
레온하르트 오일러
로 1735年에 이 級水의 값이 다음과 같다는 것을 證明하였다.

後日 이 級數는 다음과 같은 一般式으로 表現되었는데 이것이
리만 제타 函數
이다.
[39]

리만 제타 函數는 s가 짝數일 때 위 式을 利用하여 그 값을 쉽게 計算할 수 있으나 홀數일 때는 自明하지 않다. 1978年 s가 3일 때 無理數로 收斂하는 것이 證明되었다. 이 收斂값은
아페리 常數
라고 한다.
[40]
複素數 計算
[
編輯
]
 複素平面
에 그린
오일러의 公式
. 各
φ
가
π
라디안(180°)으로 增加하는 동안 오일러 等式이 成立함을 보인다.
複素平面
에 그린
오일러의 公式
. 各
φ
가
π
라디안(180°)으로 增加하는 동안 오일러 等式이 成立함을 보인다.
複素數
 는
極座標界
를 利用하여 다음과 같이 나타낼 수 있다.
[41]
는
極座標界
를 利用하여 다음과 같이 나타낼 수 있다.
[41]

複素解釋學
에서 π는 複素數 變數가
指數 函數
에서 보이는 行動과 聯關이 있으며
오일러의 公式
에 따라 다음과 같이 表現할 수 있다.

i
는
虛數 單位
利器 때문에
i
2
= ?1 이므로 이를 π
라디안
(=180°)과 함께
자연로그
의 밑
e
의 指數로 表現하면 다음과 같은
오일러 等式
을 얻는다.

따라서
n
番째
單位筋
은 다음과 같다.

이제
가우스 積分
으로 나타내면,

이 結果는
半整數
의
감마 函數
가 √π의 有理數 곱임을 뜻한다.
確率과 統計
[
編輯
]
 確率 密度 函數
f(x; x_0, γ )에 對한
코시 分布
確率 密度 函數
f(x; x_0, γ )에 對한
코시 分布
確率
과
統計
에서 圓周率이 登場하는 整理들은 다음과 같은 것들이 있다.

이 된다.
[42]

- 參考로, 모든 確率 密度 函數는 다음과 같이 積分한다.
[44]

조르주루이 르클레르 드 뷔퐁
이 提起한
뷔퐁의 바늘
問題는 圓周率의 近似값을 求하는 經驗主義的인 方法으로 擧論된다. 길이가 L인 바늘을 一定 間隔으로 그린 平行線에 떨어뜨린다고 假定해 보자. 이 때 平行線의 間隔 S가 바늘의 길이보다 크다고 하면, 바늘을 떨어뜨린 回數 n番에 對해 바늘이 平行線 밖으로 나간 回數 x番(單, x>0)에는
몬테카를로 方法
에 依해 다음과 같은 關係가 있다.
[45]

卽, 뷔퐁의 바늘 問題에서 바늘을 떨어뜨리는 回數가 매우 많아지면 바늘이 平行線을 벗어나는 回數에 對한 바늘을 떨어뜨린 全體 回數의 比는 圓周率에 近似한다.
物理學
[
編輯
]
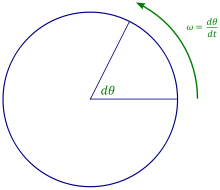 回轉하는 物體에는
角速度
가 있다
回轉하는 物體에는
角速度
가 있다
圓周率 自體는
物理 常數
가 아니지만
物理學
의 여러 分野에서 두루 使用한다. 이는
自然
現象
의 相當數가
원
과 關係가 있기 때문이다. 例를 들어 回轉數를 일정하게 維持하는 等速圓運動에서
角速度
와
原州速度
는 다음과 같이 計算할 수 있다.
[46]
- 角速度를 ω (= θ / 超), 分當 回轉數를 N이라 하면

- 이때, 半지름을 r이라 하면 原州速度 v는

이 外에 物理學에서 圓周率을 使用하는 境遇는 다음과 같다.
- 不確定性 原理
에 따라,
量子 力學
敵人
物理量
은 同時에 正確히 觀察할 수 없다. 例를 들어 粒子의 特定 位置를 Δ x라 하고 이 때의
運動量
을 Δ p 라 하면, 이 둘의 크기를 둘 다 正確히 觀察할 수는 없으며 다음 式을 使用해 確率的으로만 計算한다.
[47]


- 여기서
 은
리치 曲率
,
은
리치 曲率
,
 은
스칼라 曲率
,
은
스칼라 曲率
,
 는
計量 텐서
,
는
計量 텐서
,
 는
宇宙 常數
,
는
宇宙 常數
,
 는
重力 常數
,
는
重力 常數
,
 는
光束
, 그리고
는
光束
, 그리고
 는
에너지-運動量 텐서
이다.
는
에너지-運動量 텐서
이다.
같이 보기
[
編輯
]
註解
[
編輯
]
- ↑
 는
라디안
값이며,
六十分法
으로 나타내면 45°이다. 한便 탄젠트 函數의 값은 0일 때 0이 되며
는
라디안
값이며,
六十分法
으로 나타내면 45°이다. 한便 탄젠트 函數의 값은 0일 때 0이 되며
 , 卽 90°일 때 無限이 된다.
, 卽 90°일 때 無限이 된다.
- ↑

- ↑
이와 方式이 같은 證明 가운데
 가 無理手임을 證明한
에우클레이데스
의 證明이 널리 알려져 있다.
가 無理手임을 證明한
에우클레이데스
의 證明이 널리 알려져 있다.
- ↑
排中律은
論理學
의 基本 公理 가운데 하나로서 A이면서 同時에 A가 아닌 境遇는 없다는 것이다.
불 臺數
로 表現하면

- ↑
이 式은
바젤 問題
의 解答으로 後日
리만 제타 函數
로 一般化되었을 때
 에 該當하는 級水이다.
에 該當하는 級水이다.
各州
[
編輯
]
- ↑
송은영, 재미있는 數學常識, 맑은창, 2007,
ISBN
89-86607-59-X
, 126-133 쪽
- ↑
Pickover, Clifford A. (2005).
A passion for mathematics: numbers, puzzles, madness, religion, and the quest for reality
. John Wiley and Sons. p. 52.
ISBN
0-471-69098-8
.,
Extract of page 52
- ↑
가
나
파이(π) 本格 硏究는 아르키메데스부터
Archived
2012年 12月 9日 -
웨이백 머신
, 사이언스타임즈, 2010年 1月 20日
- ↑
"About Pi"
. Ask Dr. Math FAQ. Retrieved 2007-10-29.
- ↑
Stein, Sherman (2006). 《아르키메데스》. 飜譯 李愚英. 경문사. 170쪽.
ISBN
89-7282-926-9
.
- ↑
Smith, David Eugene.
A source book in mathematics
, Volume I, pp. 346-347.
- ↑
가
나
Pi Seems A Good Random Number Generator But Not Always The Best
, Science daily, 2005-4-25
- ↑
Rudin, Walter
(1976).
《Principles of mathematical analysis》
. International Series in Pure and Applied Mathematics (英語) 3板. McGraw-Hill.
ISBN
978-0-07-054235-8
.
MR
0385023
.
Zbl
0346.26002
. 2014年 10月 6日에
原本 文書
에서 保存된 文書
. 2014年 10月 6日에 確認함
.
- ↑
Beckmann, Petr (1976), A History of Pi, St. Martin's Griffin,
ISBN
978-0-312-38185-1
- ↑
가
나
김흥식, 世上의 모든知識, 서해문집, 2007,
ISBN
89-7483-317-4
545-546쪽
- ↑
科學東亞 2006年 7月號, 圓周率 π의 수수께끼
- ↑
장혜원, 靑少年을 위한 東洋數學社, 두리미디어, 2006,
ISBN
89-7715-160-0
, 71쪽
- ↑
나숙자, 親切한 圖形 敎科書, 부키, 2007,
ISBN
89-6051-016-5
, 243쪽
- ↑
Kaye, R.W..
"Archimedean ordered fields"
Archived
2009年 3月 16日 -
웨이백 머신
. web.mat.bham.ac.uk. Retrieved 2009-11-07.
- ↑
장혜원, 靑少年을 위한 東洋數學社, 두리미디어, 2006,
ISBN
89-7715-160-0
, 70-73쪽
- ↑
위안싱페이, 長淵 驛, 中國文明臺視野 1, 김영사, 2007,
ISBN
89-349-2736-4
, 465쪽
- ↑
中國史學會, 강영매 驛, 中國歷史博物館 4, 범우사, 2004年,
ISBN
89-08-04302-0
, 76쪽
- ↑
가
나
尖端科學과 圓周率
Archived
2013年 12月 12日 -
웨이백 머신
, 國民日報, 2005-7-11
- ↑
가
나
사이먼 싱, 박병철 驛, 페르마의 마지막 整理, 영림카디널, 2002,
ISBN
89-85055-97-6
74-75쪽
- ↑
日, 쓰쿠바 大學 世界 新記錄 圓周率 자리數 計算
, JPNews, 2009-8-18
- ↑
円周率の計算けた?で世界記?を樹立
Archived
2012年 6月 28日 -
웨이백 머신
, 쓰쿠바 大學 홈페이지 (日本語)
- ↑
파이(π), 2兆7千億 자리까지 計算
Archived
2012年 12月 9日 -
웨이백 머신
, 사이언스타임즈, 2010-1-19
- ↑
日會社員, 圓周率 小數點 以下 5兆 자리까지 計算 成功 :: 네이버 뉴스
- ↑
Peter Trub가 計算한
 값 22兆 자리 中 첫 1兆 자리의 값은
http://pi2e.ch/blog/
사이트에서 다운로드 받을 수 있다.
값 22兆 자리 中 첫 1兆 자리의 값은
http://pi2e.ch/blog/
사이트에서 다운로드 받을 수 있다.
- ↑
김흥식, 世上의 모든知識, 서해문집, 2007,
ISBN
89-7483-317-4
547쪽
- ↑
Laczkovich, Miklos (1997),
"On Lambert's proof of the irrationality of π"
, American Mathematical Monthly 104 (5): 439?443, ISSN 0002-9890
- ↑
Zhou, Li; Markov, Lubomir (2010),
"Recurrent Proofs of the Irrationality of Certain Trigonometric Values"
, American Mathematical Monthly 117 (4): 360?362
- ↑
김태성,
e 및 π의 超越成果 高等學校에서 超越數 地圖
Archived
2012年 11月 7日 -
웨이백 머신
, 韓國數學敎育學會 A 通卷 14卷 2號, 1976年, 17-22
- ↑
Hilberts Beweis der Transzendenz der Ludolphschen Zahl π
Archived
2011年 7月 16日 -
웨이백 머신
(獨逸語)
- ↑
가
나
장우석, 數學 哲學에 미치다, 숨비소리, 2008年,
ISBN
89-93265-01-1
, 174-178쪽
- ↑
Arndt, J. & Haenel, C. (2001),
Pi ? Unleashed
, Berlin: Springer, p. 3,
ISBN
3-540-66572-2
.
- ↑
나카다 노리오, 황소연 役, 피라미드에서 數學을 배우자 (數學의 도레미 3), 二智북, 2001年,
ISBN
89-89422-62-0
, 160-161쪽
- ↑
Pierre Eymard,Jean Pierre Lafon,
The number π
, 45p.
- ↑
Opera mathematica ... opera atque studio Francisci a Schooten, Leydensis, ...
- P400L17,Variorum de rebus Mathematicis Reiponiorum Liber VIII
- ↑
Lennart Berggren,Jonathan M. Borwein,Peter B. Borwein,
Pi, a source book
- ↑
Lange, L. J. (May 1999).
"An Elegant Continued Fraction for π"
. The American Mathematical Monthly 106 (5): 456?458. doi:10.2307/2589152
- ↑
Stein, Sherman (2006). 《아르키메데스》. 飜譯 李愚英. 경문사. 145-168쪽.
ISBN
89-7282-926-9
.
- ↑
가
나
박은순 (2008). 《쉬운 微分·積分學》. 崇實大學校出版部.
ISBN
89-7450-235-6
.
- ↑
존 더비셔, 박병철 驛, 《리만 假說》, 勝算,
ISBN
978-89-88907-88-7
, 99-122쪽
- ↑
Proving A Proof Is A Proof ≪ Godel’s Lost Letter and P=NP
- ↑
Smith, Julius O..
"Euler's Identity"
, Mathematics of the Discrete Fourier Transform (DFT). W3K Publishing. 0-9745607-0-7. 2011年 2月 5日에 確認.
- ↑
Gaussian Integral
, MathWorld, 2004-10-07 確認
- ↑
Cauchy Distribution
, MathWorld, 2007-11-08 確認
- ↑
Probability Function
Archived
2011年 8月 15日 -
웨이백 머신
, MathWorld, 2007-11-08 確認함
- ↑
Weisstein, Eric W (2005-12-12).
"Buffon's Needle Problem"
. MathWorld. Retrieved 2007-11-10.
- ↑
문성수, 定說 材料力學, 기전硏究社, 2000年,
ISBN
89-336-0539-8
, 52-53쪽
- ↑
존 테일러, 강희재 外 驛, 現代物理學, 敎保文庫, 2005,
ISBN
89-7085-543-2
, 242-244쪽
- ↑
Einstein, Albert (1916).
"The Foundation of the General Theory of Relativity"
Archived
2006年 8月 29日 -
웨이백 머신
(PDF). Annalen der Physik.
外部 링크
[
編輯
]
|
|---|
| 精髓
| |
|---|
| 虛數
|
- i
(
 ) )
|
|---|
| 超越數
|
- π
- e
(
 ) )
|
|---|
| 無理手
| |
|---|
| 기타
| |
|---|