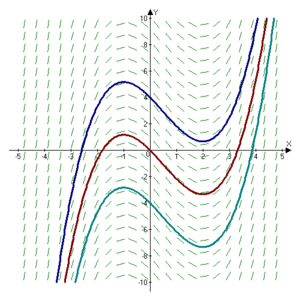
 의
기울기腸
에 그려진 函數
의
기울기腸
에 그려진 函數
 의 세 가지 圓函數
의 세 가지 圓函數
 . 積分 常數는
. 積分 常數는
 .
.
微積分學
에서
不定積分
(不定積分,
英語
:
indefinite integral
)은 어떤
函數
를
導函數
로 하는 모든 函數를 求하는 演算이다. 否定的분이 存在할 境遇, 이는 恒常 固定된 函數와 任意의 常數의 合意 꼴로 나타낼 수 있다. 따라서 常數만큼의 車를 無視하면 不定積分은
微分
또는
導函數
를 求하는 演算의 逆演算이다.
正義
[
編輯
]
函數
 (
(
 )가 주어졌을 때, 萬若 다음 條件을 만족시키는 函數
)가 주어졌을 때, 萬若 다음 條件을 만족시키는 函數
 (
(
 )가 存在한다면, 이를
)가 存在한다면, 이를
 의
圓函數
(原函數,
英語
:
antiderivative
) 또는
逆導函數
(逆導函數)라고 한다.
의
圓函數
(原函數,
英語
:
antiderivative
) 또는
逆導函數
(逆導函數)라고 한다.

函數
 (
(
 )의 한 圓函數
)의 한 圓函數
 가 存在할 境遇,
가 存在할 境遇,
 의 모든 圓函數는 正確히 다음과 같다.
의 모든 圓函數는 正確히 다음과 같다.

이를
 의
不定積分
이라고 한다. 여기서
의
不定積分
이라고 한다. 여기서
 는 任意의 常數이며, 이를
積分常數
라고 부른다. 否定的분이 恒常 위와 같은 꼴임은 다음과 같이 證明할 수 있다. 于先 任意의 常數
는 任意의 常數이며, 이를
積分常數
라고 부른다. 否定的분이 恒常 위와 같은 꼴임은 다음과 같이 證明할 수 있다. 于先 任意의 常數
 에 對하여,
에 對하여,
 이므로,
이므로,
 이다. 卽,
이다. 卽,
 는
는
 의 圓函數이다. 또한 任意의 圓函數
의 圓函數이다. 또한 任意의 圓函數
 에 對하여,
에 對하여,
 이므로,
平均값 整理
에 따라
이므로,
平均값 整理
에 따라
 는 常數 函數이다. 따라서
는 常數 函數이다. 따라서
 는
는
 꼴로 나타낼 수 있다.
꼴로 나타낼 수 있다.
위와 같은 꼴의 不定積分 公式은 定義域을 이루는 各各의 區間에서만 有效하다. 例를 들어,
 에 對한 다음과 같은 不定積分 公式이 成立하려면 두 區間
에 對한 다음과 같은 不定積分 公式이 成立하려면 두 區間
 및
및
 가운데 하나를 選擇하여야 한다.
[1]
:398-399
가운데 하나를 選擇하여야 한다.
[1]
:398-399

全體 定義域
 에서의 實際 不定積分은 다음과 같다.
[1]
:398-399
에서의 實際 不定積分은 다음과 같다.
[1]
:398-399

性質
[
編輯
]
微分과의 關係
[
編輯
]
萬若
 의 否定的분이 存在한다면 다음이 成立한다.
의 否定的분이 存在한다면 다음이 成立한다.

萬若
 가
微分 可能 函數
라면 다음이 成立한다.
가
微分 可能 函數
라면 다음이 成立한다.

이에 따라 常數 車를 無視하면 不定積分은 微分의 逆演算이다.
微積分學의 基本 整理
[
編輯
]
連續 函數
 의 한 圓函數는 積分上限을 變數로 醉한 定積分으로 나타낼 수 있다.
의 한 圓函數는 積分上限을 變數로 醉한 定積分으로 나타낼 수 있다.

反對로,
連續 函數
 의 한 圓函數
의 한 圓函數
 가 주어졌을 때, 定積分은 다음과 같이 나타낼 수 있다.
가 주어졌을 때, 定積分은 다음과 같이 나타낼 수 있다.

線型性
[
編輯
]
函數
 의 否定的분이 存在한다면,
의 否定的분이 存在한다면,
 의 不定積分 亦是 存在하며, 다음이 成立한다.
의 不定積分 亦是 存在하며, 다음이 成立한다.

函數
 의 否定的분이 存在한다면, 常數
의 否定的분이 存在한다면, 常數
 에 對하여
에 對하여
 의 不定積分 亦是 存在하며,
의 不定積分 亦是 存在하며,
 일 境遇 다음이 成立한다.
일 境遇 다음이 成立한다.

이에 따라 不定積分은
線型
演算이다.
置換 積分
[
編輯
]
萬若
 의 한 圓函數
의 한 圓函數
 가 存在하며,
가 存在하며,
 가 微分 可能 函數라면, 다음이 成立한다.
[2]
:246, 整理6.2.1
가 微分 可能 函數라면, 다음이 成立한다.
[2]
:246, 整理6.2.1

萬若
 가 微分 可能 函數이며,
가 微分 可能 函數이며,
 가 成立하며,
가 成立하며,
 의 한 圓函數
의 한 圓函數
 가 存在한다면, 다음이 成立한다.
[2]
:252, 整理6.2.2
가 存在한다면, 다음이 成立한다.
[2]
:252, 整理6.2.2

部分 積分
[
編輯
]
萬若
 가 微分 可能 函數이며,
가 微分 可能 函數이며,
 의 否定的분이 存在한다면, 다음이 成立한다.
의 否定的분이 存在한다면, 다음이 成立한다.

예
[
編輯
]
有理 函數
[
編輯
]
모든 (
失手
)
有理 函數
는 多項式과 眞分數式의 合으로 나타낼 수 있으며, 모든 眞分數式은
部分 分數 分解
를 통해 다음과 같은 꼴의 分數式들의 合으로 나타낼 수 있다.


여기서
 은 失手이며
은 失手이며
 은 陽의 精髓이다. 또한
은 陽의 精髓이다. 또한
 을 만족시킨다. 이 두 가지 分數式의 不定積分은 다음과 같이 求할 수 있다.
을 만족시킨다. 이 두 가지 分數式의 不定積分은 다음과 같이 求할 수 있다.





部分 分數 分解의 各 項이 初等 函數이므로, 모든 有理 函數의 不定積分은 初等 函數이다.
三角 有理 函數
[
編輯
]
三角 有理 函數는
 꼴의 函數를 뜻한다. 여기서
꼴의 函數를 뜻한다. 여기서
 는 2變數 有理 函數이다. 이에 對한 否定的分에 다음과 같은 置換 積分을 使用하자.
는 2變數 有理 函數이다. 이에 對한 否定的分에 다음과 같은 置換 積分을 使用하자.

그러면 元來의 不定積分은 有理 函數의 不定積分으로 變한다.

萬若
 라면, 이는 恒常
라면, 이는 恒常
 꼴로 나타낼 수 있다. 따라서 이 境遇 다음과 같은 더 簡便한 技法을 使用할 수 있다.
꼴로 나타낼 수 있다. 따라서 이 境遇 다음과 같은 더 簡便한 技法을 使用할 수 있다.

마찬가지로, 萬若
 라면, 이는
라면, 이는
 꼴이므로, 이 境遇 普通 다음과 같은 技法이 더 簡便하다.
꼴이므로, 이 境遇 普通 다음과 같은 技法이 더 簡便하다.

萬若
 라면,
라면,
 꼴이므로, 이 境遇 普通 다음과 같은 技法이 더 簡便하다.
꼴이므로, 이 境遇 普通 다음과 같은 技法이 더 簡便하다.

事實 모든 有理 函數는 위와 같은 세 有理 函數의 合으로 다음과 같이 나타낼 수 있다.

無理 函數
[
編輯
]
無理 函數의 不定積分은 初等 函數가 아닐 수 있다. 그러나 다음과 같은 꼴의 不定積分은 初等函數이다.
![{\displaystyle R\left(x,{\sqrt[{n}]{\frac {ax+b}{cx+d}}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc1ce2cc8f8f9bbd84121c010863f02cf812d584)
여기서
 는 2變數 有理 函數이며,
는 2變數 有理 函數이며,
 는 陽의 精髓이며,
는 陽의 精髓이며,
 는 失手이다. 또한
는 失手이다. 또한
 을 만족시킨다. 다음과 같은 置換 積分을 使用하자.
을 만족시킨다. 다음과 같은 置換 積分을 使用하자.
![{\displaystyle {\sqrt[{n}]{\frac {ax+b}{cx+d}}}=t,\;x={\frac {dt^{n}-b}{a-ct^{n}}},\;\mathrm {d} x={\frac {n(ad-bc)t^{n-1}}{(a-ct^{n})^{2}}}\mathrm {d} t}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19e1a41234ba327ad0462ba879ce6ab2b15ccbe8)
그러면 元來의 不定積分은 有理 函數의 不定積分으로 變한다.
![{\displaystyle \int R\left(x,{\sqrt[{n}]{\frac {ax+b}{cx+d}}}\right)\mathrm {d} x=\int R\left({\frac {dt^{n}-b}{a-ct^{n}}},t\right){\frac {n(ad-bc)t^{n-1}}{(a-ct^{n})^{2}}}\mathrm {d} t}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4337bb3f28082b6bab23337663c025ba6411944f)
函數
 를 생각하자. 여기서
를 생각하자. 여기서
 는 失手이며,
는 失手이며,
 는 有理數이다.
는 有理數이다.
 가운데 적어도 하나가 整數일 境遇 이 不定積分은 初等 函數가 된다.
가운데 적어도 하나가 整數일 境遇 이 不定積分은 初等 函數가 된다.
 이며
이며
 라고 하자. 여기서
라고 하자. 여기서
 는 精髓이다. 萬若
는 精髓이다. 萬若
 일 境遇, 函數에 나오는 제곱根式은
일 境遇, 函數에 나오는 제곱根式은
![{\displaystyle {\sqrt[{s'}]{z}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92e3632862cbf2f23f656d7aa0a8aea545d32d10) 뿐이므로, 置換 積分
뿐이므로, 置換 積分
![{\displaystyle {\sqrt[{s'}]{z}}=t}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14111933807a7880cb5e80fab91c1990c2f0e42c) 를 통해 求할 수 있다. 萬若
를 통해 求할 수 있다. 萬若
 일 境遇, 函數에 나오는 제곱根式은
일 境遇, 函數에 나오는 제곱根式은
![{\displaystyle {\sqrt[{s}]{a+bz}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f6a28d18ae30f610cf3ae09b1111391463cc31e) 뿐이므로, 亦是 置換 積分
뿐이므로, 亦是 置換 積分
![{\displaystyle {\sqrt[{s}]{a+bz}}=t}](https://wikimedia.org/api/rest_v1/media/math/render/svg/803fae17b804fe612ff45b4af31000cfd00b52bc) 를 통해 求할 수 있다. 萬若
를 통해 求할 수 있다. 萬若
 일 境遇, 函數를
일 境遇, 函數를
 와 같이 變形하였을 때 제곱根式은
와 같이 變形하였을 때 제곱根式은
![{\displaystyle \textstyle {\sqrt[{s}]{(a+bz)/z}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9214214696b50be617dc58a85bc122e7e319a74) 뿐이므로, 置換 積分
뿐이므로, 置換 積分
![{\displaystyle \textstyle {\sqrt[{s}]{(a+bz)/z}}=t}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aab24390fbfb2ea114f3573f05baf7466c4fa0c6) 를 통해 求할 수 있다.
를 통해 求할 수 있다.
보다 一般的으로, 函數
 를 생각하자. 여기서
를 생각하자. 여기서
 는 失手이며,
는 失手이며,
 는 有理數이다. 다음과 같은 置換 積分을 使用하자.
는 有理數이다. 다음과 같은 置換 積分을 使用하자.

그러면 위와 같은 꼴의 函數의 不定積分으로 變한다.

따라서
 가운데 적어도 하나가 整數일 境遇 이 不定積分은 初等 函數이다. 反對로
가운데 적어도 하나가 整數일 境遇 이 不定積分은 初等 函數이다. 反對로
 가 整數가 아닐 境遇 이 不定積分은 初等 函數로 나타낼 수 없음을 19世紀 中葉에
파프累티 체비쇼프
가 證明하였다.
가 整數가 아닐 境遇 이 不定積分은 初等 函數로 나타낼 수 없음을 19世紀 中葉에
파프累티 체비쇼프
가 證明하였다.
初等 函數로 나타낼 수 없는 不定積分
[
編輯
]
初等 函數
의 不定積分은 初等 函數가 아닐 수 있다. 例를 들어, 다음과 같은 否定的분들은 初等 函數가 아니다.
- (
誤差 函數
)

- (
프레넬 函數
)

- (
三角 積分 函數
)

- (
로그 積分 函數
)



같이 보기
[
編輯
]
各州
[
編輯
]