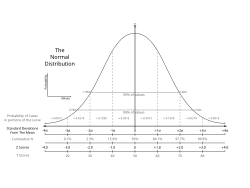
 Normaalijakauma
on tilastotieteessa usein kaytetty tyokalu.
Normaalijakauma
on tilastotieteessa usein kaytetty tyokalu.
Tilastotiede
on
todennakoisyyslaskentaan
perustuva
tieteenala
, joka tutkii
tilastollisten
aineistojen keraamista, kasittelya ja talta pohjalta tehtavaa
paattelya
.
[1]
Tilastotieteen avulla voidaan mitata havaintoja ja kasitella mittausten muodostamia aineistoja, ja tilastotiede tuo siten
empiriaa
erilaisiin tutkimuksiin. Tilastotieteen tulosten pohjalta tehtava paattely on
induktiivista paattelya
eli aineiston pohjalta pyritaan yleistamaan asioita yksittaisesta yleiseen. Havaintoaineistoja voidaan myos hankkia tietylla aikavalilla eli tuottaa
aikasarja
. Tilastotiede voidaan jakaa teoreettiseen ja soveltavaan tilastotieteeseen. Tilastotiedetta kaytetaan tilastollisten tutkimusten tekemiseen ja nama jaetaan maarallisiin (kvantitatiivisiin) ja laadullisiin (kvalitatiivisiin) tutkimuksiin. Tilastotieteen harjoittajaa kutsutaan
tilastotieteilijaksi
.
Tilastotiedetta sovelletaan monilla tutkimusaloilla, joihin kuuluvat esimerkiksi
luonnon
-,
yhteiskunta
- ja
humanistiset tieteet
. Tilastollisella paattelylla on tarkea osuus tieteellisessa
hypoteesin testauksessa
. Tilastotiedetta kaytetaan myos teollisuudessa. Tilastotiedetta hyodynnetaan myos valtion ja kuntien virallisissa tilastoissa seka kansantalouden tilan selvittamisessa, ja historiallisesti julkinen valta oli ensimmainen tilastojen hyodyntaja. Vuonna 1749 laadittiin Suomen ensimmainen vaestotilasto.
[2]
Suomessa
Tilastokeskus
tuottaa valtaosan Suomen virallisista tilastoista.
[3]
Muita
tilastoviranomaisia
Suomessa ovat
Terveyden ja hyvinvoinnin laitos
,
Luonnonvarakeskus
seka
Tulli
. Myos
Suomen Pankki
tuottaa merkittavan maaran virallisia tilastoja.
[4]
Kun tilastotieteen menetelmia kaytetaan havaitun aineiston esittamiseen, on kyse kuvailevasta tilastotieteesta. Kun kuvailusta siirrytaan aineiston tarkasteluun tai
mallinnukseen
siten, etta aineiston epavarmuus ja havaintojen satunnaisuus otetaan huomioon, puhutaan
tilastollisesta paattelysta
. Naissa molemmissa tapauksissa on kyse soveltavasta tilastotieteesta.
Matemaattinen tilastotiede
keskittyy puolestaan tarkastelemaan tilastotieteen teoreettista perustaa. Tilastotieteessa keskeisia asioita ovat otantamenetelmat, mitta-asteikot, keskiluvut seka vaihtelun ja riippuvuuden tunnusluvut. Tilastollisten tutkimusten tekeminen edellyttaa suunnitelmallisuutta tutkimussuunnitelman muodossa, koska se luo pohjan sille, mita keratysta aineistoista voidaan lopulta saada irti.
Tilastotieteen soveltaminen tarkasteltavaan tieteelliseen, teolliseen tai yhteiskunnalliseen ongelmaan alkaa
populaation
maarittelylla. Kyseessa voi olla jonkin
maan
vaesto
tai
tehtaan
valmistamat
tuotteet
. Toisaalta voidaan havainnoida aineistoa tuottava
prosessi
eri ajankohtina, jolloin kyseessa on
aikasarja
.
Aineistoa on tavallisesti mahdollista kerata vain populaation osajoukosta, jolloin tutkimuksen kohteena on
otos
. Otoksesta voidaan kerata aineistoa joko havainnoiden tai kokeellisessa asetelmassa. Kun aineisto on keratty, siita tehtava analyysi voidaan jakaa kuvailuun ja paattelyyn, jotka tosin liittyvat usein toisiinsa laheisesti.
Otannalla tarkoitetaan tutkimukseen mukaan tulevien tutkimusyksikoiden valitsemista perusjoukosta.
Otannan tavoitteena on saada mahdollisimman edustava otos koko perusjoukosta, jotta paattely voitaisiin yleistaa koskemaan myos perusjoukkoa.
[5]
Otantamenetelman valinnalla voi olla suuri vaikutus tutkimuksen onnistumiseen.
 Esimerkki
yksinkertaisesta satunnaisotannasta
.
Esimerkki
yksinkertaisesta satunnaisotannasta
.
Yksinkertainen ja hyvin yleisesti kaytetty otantamenetelma on
yksinkertainen satunnaisotanta
. Yksinkertaisessa satunnaisotannassa jokaisella perusjoukon yksikolla on yhta suuri todennakoisyys tulla valituksi otokseen. Toinen yksinkertainen otantamenetelma on
systemaattinen otanta
, jossa listatusta aineistosta valitaan tietyin valein yksikko mukaan tutkimukseen.
[6]
Monesti yksinkertaisimmat menetelmat eivat kuitenkaan tuota parasta mahdollista lopputulosta. Mikali esimerkiksi tavoitteena on selvittaa haastattelututkimuksella kaikkien Suomen kolmasluokkalaisten oppilaiden aidinkielen osaamista, olisi tutkijoilla todella kova tyo kiertaa kaikki koulut, joista oppilaita valittiin mukaan tutkimukseen. Tallaisissa tapauksissa kaytetaan usein
ryvasotantaa
. Ryvasotannassa aineisto jaetaan ryhmiin ja varsinainen otanta tapahtuu naiden ryhmien valilla. Esimerkin tapauksessa voitaisiin jakaa perusjoukko ryhmiin koululuokan perusteella ja arpoa, mitka luokat valitaan kokonaisuudessaan mukaan tutkimukseen.
[6]
Perusjoukko voidaan usein jakaa toisensa poissulkeviin osajoukkoihin. Esimerkiksi tehtaessa tutkimusta siita, ovatko yliopisto-opiskelijat tyytyvaisia paaaineeseensa, voitaisiin ajatella, etta tutkimukseen halutaan mukaan kaikkien alojen opiskelijoita. Yksinkertaista satunnaisotantaa kaytettaessa aloilta, joilla on vahan opiskelijoita, ei valttamatta tulisi lainkaan opiskelijoita mukaan tutkimukseen. Taman estamiseksi voitaisiin etukateen paattaa, kuinka monta opiskelijaa halutaan mukaan kultakin alalta ja suorittaa sitten yksinkertainen satunnaisotanta kunkin alan opiskelijoiden kesken. Tata kutsutaan
ositetuksi otannaksi
. Ositetussa otannassa on oleellista huomioida, etta havaitusta aineistosta lasketut
tunnusluvut
eivat valttamatta edusta koko perusjoukkoa. Tama on usein korjattavissa painotuksella.
[6]
Otantaa voidaan tehda myos siten, etta kunkin yksikon todennakoisyys tulla valituksi riippuu jostain taman yksikon ominaisuudesta, kuten koosta. Esimerkiksi tehtaessa tutkimusta koko Suomen tyottomyydesta yksittaisten kuntien tyottomyysprosenttien perusteella on hyvin oleellista, etta isoimmat kunnat tulevat valituksi mukaan. Nain ollen voidaan ajatella, etta isommilla kunnilla tulisi olla suurempi todennakoisyys tulla valituksi. Tata kutsutaan
otannaksi tilastoyksikon koon mukaan
.
[6]
 Muuttujien jakaumien tarkastelu ja vertailu onnistuu katevasti
viiksilaatikkokuvaajan
avulla. Kuvaaja koostuu laatikosta ja viiksista, missa laatikon ylareuna kuvaa jarjestetyn aineiston ylaneljannesta ja alareuna alaneljannesta siten, etta 25 % aineistosta jaa laatikon ylapuolelle ja 25 % laatikon alapuolelle. Laatikon sisalla oleva viiva kuvaa aineiston mediaania ja viiksien paat vastaavat aineiston minimia ja maksimia.
Muuttujien jakaumien tarkastelu ja vertailu onnistuu katevasti
viiksilaatikkokuvaajan
avulla. Kuvaaja koostuu laatikosta ja viiksista, missa laatikon ylareuna kuvaa jarjestetyn aineiston ylaneljannesta ja alareuna alaneljannesta siten, etta 25 % aineistosta jaa laatikon ylapuolelle ja 25 % laatikon alapuolelle. Laatikon sisalla oleva viiva kuvaa aineiston mediaania ja viiksien paat vastaavat aineiston minimia ja maksimia.
Kuvaileva tilastollinen analyysi on havaitun aineiston esittamista joko numeerisesti tai graafisesti. Havaitusta aineistosta voidaan laskea
tunnuslukuja
, jotka kuvaavat muuttujien ominaisuuksia, kuten sijaintia, hajontaa, vinoutta tai huipukkuutta.
Tyypillisia sijaintia kuvaavia tunnuslukuja ovat
moodi
,
minimi
,
maksimi
,
mediaani
,
kvantiilit
, seka erilaiset
keskiarvot
. Usein kaytettyja vaihtelua kuvaavia tunnuslukuja ovat
keskihajonta
,
varianssi
,
kvartiilivali
ja
vaihteluvali
. Yleinen tapa esittaa aineistoa tiivistetysti on esittaa kustakin muuttujasta minimi, maksimi, ala- ja ylakvartiilit seka mediaani.
[5]
Naista viidesta tunnusluvusta piirrettya kuvaajaa kutsutaan
viiksilaatikkokuvaajaksi
. Yksittaisen muuttujan jakaumaa voidaan kuvailla graafisesti esimerkiksi
histogrammilla
. Histogrammin sijasta voidaan kayttaa myos
ydinestimaattoria
, joka voidaan nahda histogrammin yleistyksena.
Usein ollaan kiinnostuneita myos kahden tai useamman muuttujien valisista riippuvuussuhteista. Lineaarista riippuvuutta voidaan mitata esimerkiksi
kovarianssilla
tai
korrelaatiolla
. Muita riippuvuutta kuvaavia tunnuslukuja ovat muun muassa
Kendallin jarjestyskorrelaatiokerroin
ja
Spearmanin jarjestyskorrelaatiokerroin
. Kahden muuttujan valista riippuvuutta voidaan havainnollistaa graafisesti
sirontakuviolla
.
Tilastollisessa paattelyssa pyritaan yleistamaan aineiston perusteella saatuja tuloksia koko perusjoukkoon. Havaintoihin liittyy usein satunnaisuutta ja tilastollisen paattelyn tavoitteena onkin selvittaa, etta voiko aineistossa havaittu ilmio selittya pelkalla satunnaisvaihtelulla. Paattelyyn voi kuulua esimerkiksi mallin parametrien
estimointi
seka
tunnuslukujen
laskeminen ja niiden
tilastollisen merkitsevyyden
testaus.
Hyvin suuri osa tilastollisen paattelyn teoriasta nojaa uskottavuuteen. Uskottavuudella tarkoitetaan sita, kuinka todennakoista on havaita havaitun kaltaisia arvoja asetetusta, kiinteasta mallista. Uskottavuutta mitataan uskottavuusfunktiolla

joka tulkitaan parametrin
 funktiona. Uskottavuuspaattelyn perusidea on se, etta uskottavuusfunktion arvo on suuri niille parametrin
funktiona. Uskottavuuspaattelyn perusidea on se, etta uskottavuusfunktion arvo on suuri niille parametrin
 arvoille, joista aineisto on todella peraisin. Usein oletetaan, etta havainnot ovat riippumattomia ja samoin jakautuneita. Talloin havaintoihin
arvoille, joista aineisto on todella peraisin. Usein oletetaan, etta havainnot ovat riippumattomia ja samoin jakautuneita. Talloin havaintoihin
 perustuva uskottavuusfunktio voidaan kirjoittaa
perustuva uskottavuusfunktio voidaan kirjoittaa

jossa
 on kunkin satunnaismuuttujan
on kunkin satunnaismuuttujan
 uskottavuusfunktio, eli jatkuvilla muuttujilla
tiheysfunktio
ja diskreeteilla muuttujilla
pistetodennakoisyysfunktio
.
[7]
uskottavuusfunktio, eli jatkuvilla muuttujilla
tiheysfunktio
ja diskreeteilla muuttujilla
pistetodennakoisyysfunktio
.
[7]
Uskottavuusfunktio on hyvin paljon kaytetty tyokalu seka
frekventistisessa
etta
Bayesilaisessa
tilastotieteessa.
[7]
[8]
Frekventistisessa tilastotieteessa
ajatellaan, etta tapahtuman todennakoisyys on tapahtuman suhteellinen osuus, kun toistojen maara lahestyy aaretonta. Nain ollen todennakoisyys on maaritelty vain toistettavissa olevien tilanteiden mielessa. Esimerkiksi mallien parametrit ajatellaan kiinteiksi luvuiksi, joilla ei siis ole
todennakoisyysjakaumaa
. Sen sijaan frekventistisessa paattelyssa lasketaan usein, etta kuinka todennakoista on havaita havaitun kaltaisia tunnuslukujen arvoja jostain tietysta tilanteesta.
Suuri osa nykyaan kaytossa olevista tilastotieteen kasitteista, kuten
harha
,
tunnusluvun
keskivirhe
,
p-arvo
ja
luottamusvali
, on alun perin maaritelty frekventistisessa tilastotieteessa.
[7]
Bayesilainen tilastotiede perustuu
Bayesin teoreemaan
, joka maarittelee ehdollisen todennakoisyyden:
 .
.
Bayesin teoreemassa yhdistetaan aineistosta
 laskettava uskottavuus
laskettava uskottavuus
 parametrien
parametrien
 priorijakaumaan
priorijakaumaan
 , jolloin saadaan parametreille
, jolloin saadaan parametreille
 posteriorijakauma
posteriorijakauma
 . Haluttu tilastollinen paattely tehdaan taman posteriorijakauman perusteella. Bayesilaisessa tilastotieteessa siis ajatellaan, etta tilastollisiin tunnuslukuihin ja malliparametreihin liittyy epavarmuutta, jota voidaan kuvata
todennakoisyysjakaumien
avulla.
. Haluttu tilastollinen paattely tehdaan taman posteriorijakauman perusteella. Bayesilaisessa tilastotieteessa siis ajatellaan, etta tilastollisiin tunnuslukuihin ja malliparametreihin liittyy epavarmuutta, jota voidaan kuvata
todennakoisyysjakaumien
avulla.
Bayesilaiseen tilastotieteeseen liittyy oleellisesti priorijakauman maarittaminen, joka kuvastaa maarittajan ennakkotietoa kiinnostuksen kohteena olevasta parametrista. Bayesilaista tilastotiedetta onkin usein kritisoitu ennakkotiedon sisallyttamisesta priorijakaumaan, mutta maarittamalla priorijakauma sopivasti saadaan sen merkitys posteriorijakaumaan hyvin pieneksi tai jopa olemattomaksi. Monet Bayesilaista tilastotiedetta harjoittavat eivat kuitenkaan pida ennakkotiedon kayttoa priorijakauman valitsemisessa ongelmana, vaan pikemminkin tyokaluna, jolla mallinnuksessa voidaan hyodyntaa esimerkiksi edellisia tutkimustuloksia samalta alalta.
[9]
 Esimerkki yksinkertaisesta
lineaarisesta regressiomallista
.
Esimerkki yksinkertaisesta
lineaarisesta regressiomallista
.
Tilastollinen malli on todennakoisyysjakauma, jonka avulla pyritaan tekemaan paatelmia kayttaen hyodyksi havaittua aineistoa.
[10]
Mallintamisessa ollaan usein kiinnostuneita siita, miten yhden tai useamman muuttujan arvot keskimaarin muuttuvat, kun muiden muuttujien arvo muuttuu. Tilastollista mallintamista voidaan esimerkiksi hyodyntaa sen tutkimisessa, kasvavatko kuukausitulot keskimaarin, kun koulutuksen kesto pitenee. Tilastollista mallintamista voidaan tehda seka frekventistisesta etta Bayesilaisesta nakokulmasta.
[10]
Usein kaytettyja mallinnusmenetelmia ovat muun muassa
Tilastollisilla testeilla testataan tunnusluvuille tai parametreille asetettuja
hypoteeseja
.
Tilastollisessa testissa
lasketaan ensin havaittu testisuureen arvo aineistosta ja sen jalkeen lasketaan
p-arvo
, eli todennakoisyys havaita vahintaan nain poikkeavia testisuureen arvoja
nollahypoteesin
ollessa totta. Mikali todennakoisyys havaita vahintaan nain poikkeavia testisuureen arvoja nollahypoteesin ollessa voimassa on alle ennalta asetetun merkitsevyystason, voidaan nollahypoteesi hylata valitulla merkitsevyystasolla. Mikali
p-arvo
on yli merkitsevyystason, niin voidaan todeta, etta ei ole nayttoa siita, ettei nollahypoteesi olisi voimassa. Huomion arvoista on, ettei yli merkitsevyystason olevaa p-arvoa voida tulkita niin, etta nollahypoteesi on totta. Merkitsevyystaso kuvaa testin todennakoisyytta hylata nollahypoteesi virheellisesti. Tyypillisesti kaytettyja merkitsevyystasoja ovat 10 %, 5 %, 1 % ja 0,1 %.
[5]
Testin voima on oleellinen kasite tilastollisessa testaamisessa. Testin voima on todennakoisyys, milla nollahypoteesi hylataan kun vaihtoehtoinen hypoteesi on tosi. Nain ollen mita lahempana lukua 1 testin voima on, sita herkemmin testi havaitsee eroavaisuuden nollahypoteesista.
[5]
Yleisesti kaytettyja tilastollisia testeja ovat muun muassa
Monesti testisuureen otantajakauma on hankala tai jopa mahdoton laskea. Talloin voidaan kayttaa laskennallisia menetelmia, kuten nollahypoteesin mukaisen jakauman
simulointia
tai pelkkaan havaittuun aineistoon perustuvaa
bootstrap
-menetelmaa.
[5]
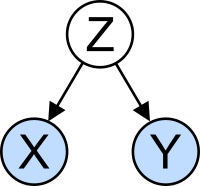 Graafinen kuvaus muuttujien X, Y, Z valisesta kausaalisuhteesta. Z vaikuttaa molempiin muuttujiin X ja Y, joilla ei kuitenkaan ole suoraa kausaalivaikutusta toisiinsa.
Graafinen kuvaus muuttujien X, Y, Z valisesta kausaalisuhteesta. Z vaikuttaa molempiin muuttujiin X ja Y, joilla ei kuitenkaan ole suoraa kausaalivaikutusta toisiinsa.
Tilastotieteessa on tarkeaa tehda ero kausaliteetin ja
korrelaation
valilla. Kausaliteetti eli syy-seuraussuhde tarkoittaa tilastollisessa yhteydessa, etta yhden muuttujan arvosta seuraa toisen muuttujan arvo.
lahde?
Kahden muuttujan valinen korrelaatio taas tarkoittaa, etta niiden arvot vaihtelevat aineistossa yhdessa, mutta kausaliteetin suuntaan ei oteta kantaa. Esimerkiksi tulojen ja elinian tutkimus voi osoittaa, etta rikkaat elavat koyhia pidempaan. Talloin tulot ja elinika ovat aineistossa korreloituneita. Tasta ei voida kuitenkaan johtaa kausaalisuhdetta, jonka mukaan varallisuus lisaisi elinikaa. Korrelaatio voi syntya kolmannen havaitsemattoman muuttujan vaikutuksesta, joka saattaisi olla esimerkiksi terveyspalveluiden saatavuus.
Perinteisesti ollaan ajateltu, etta kausaalipaattely on mahdollista vain siina tapauksessa, etta selittavan muuttujan arvoja pystytaan kontrolloimaan.
[11]
Viime aikoina ollaan kuitenkin pyritty kehittamaan menetelmia, joilla kausaalipaattelya pystytaan tekemaan myos havainnoivassa tutkimuksessa. Pearlin
kausaalimalli
perustuu ajatukseen siita, etta muuttujien valiset vuorovaikutukset ja niiden suunta tunnetaan ja taman perusteella pystytaan joissain tapauksissa
kausaalilaskennan
saannoilla poistamaan tarve kontrolloida selittavan muuttujan arvoja.
[12]
Lotossa pelaaja valitsee yhteen riviinsa seitseman numeroa 39 vaihtoehdon joukosta. Arvonnassa 39 numeron joukosta valitaan 7 numeroa ja 3 lisanumeroa. Voittoluokat ovat 7 oikein, 6 oikein + lisanumero, 6 oikein, 5 oikein ja nelja oikein. Tarkasteltaessa sita, kuinka monta erilasta lottorivia on olemassa, on selvitettava kuinka monella tavalla seitseman numeroa voidaan valita 39 joukosta. 39 numerosta voidaan muodostaa 39*38*37*...*2*1 erilaista yhdistelmaa. Lukusarjaa kutsutaan 39:n kertomaksi, 39!. Vastaavasti seitsemasta luvusta voidaan muodostaa 7! erilaista yhdistelmaa. Riviin kuulumattomat 32 numeroa voidaan valita 32! eri tavalla. Erilaisten seitseman numeroa sisaltavien rivien maara voidaan laskea seuraavasti: 39!/(7!*32!) = 15 380 937. Erilaisia lottoriveja on siis reilut 15 miljoonaa. Samalla laskukaavalla voidaan selvittaa myos kuinka monta erilaista voittoyhdistelmaa on. Erilaisia nelja oikein yhdistelmia voidaan seitseman oikean numeron joukosta muodostaa 7!/(4!*3!) = 35 kappaletta. Arpomatta jaaneet kolme numeroa voidaan lisaksi valita 32!/(3!*29!) = 4 960 tavalla. Erilaisten nelja oikein rivien maara saadaan naiden tulosten tulona eli 35*4 960 = 173 600. Samalla kombinaatioihin perustuvalla menetelmalla saadaan erilaisten voittoyhdistelmien lukumaarat:
7 oikein 1
6+1 oikein 21
6 oikein 203
5 oikein 10 416
4 oikein 173 600
Todennakoisyys sille, etta yhdella rivilla voittaa yhdella kierroksella jotain voidaan laskea jakamalla kaikkien voittoyhdistelmien summa erilaisten rivien lukumaaralla eli (1 + 21 + 230 + 10 416+ 173 600) / 15 380 937 = 0.012 eli hieman yli 1%. Koska jokaisella rivilla tapahtuu varmasti jompikumpi tapahtuma, joko tulee voitto tai ei tule voittoa, on niiden yhteenlaskettu todennakoisyys yksi. Todennakoisyys olla voittamatta mitaan voidaan laskea vahentamalla voittotodennakoisyys yhdesta. Yhden rivin todennakoisyys olla voittamatta on siis 1 - 0.012 = 0.988 eli 98.8%.
[13]
Laaketieteellisissa tutkimuksissa kaytetaan (esim. syopakasvaimia etsittaessa) apuna tietokonetomografiaa. Menetelman avulla ihmisen kudoksista tai elimista tuotetaan tomografi-nimisella laitteella ns. viipale- tai tasokuvia. Kuvat perustuvat sahkomagneettisen tai hiukkassateilyn mittaamiseen sateilyn kulkiessa kudosten tai elinten lapi. Kuvaa muodostettaessa tomografiin ohjelmoitu algoritmi ratkaisee inversio-ongelmaksi kutsutun matemaattisen ongelman, joka voidaan luontevimmin tulkita Bayeslaisten tilastollisten menetelmien
muodostamassa kehikossa.
[14]
 Kyselytutkimuksen tulos pylvasdiagrammilla esitettyna
Kyselytutkimuksen tulos pylvasdiagrammilla esitettyna
Kyselytutkimusten suunnittelussa, toteutuksessa ja tulosten analysoinnissa sovelletaan tilastollisista menetelmista mm. otantaa, estimointia ja testausta. Esimerkiksi ihmisten mielipiteita erilaisiin yhteiskuntaa koskeviin kysymyksiin voidaan selvittaa kyselytutkimuksilla. Kohteeksi poimitaan tyypillisesti 1000 ? 2000 suomalaista, ja tavoitteena on tehda kyselyn tulosten perusteella johtopaatoksia mielipiteiden jakautumisesta kaikkien suomalaisten joukossa. Kyselyn tulokset voidaan yleistaa koskemaan kaikkia suomalaisia, jos kyselyn kohteiksi poimittujen suomalaisten joukko muodostaa edustavan pienoiskuvan suomalaisista. Pienoiskuva on edustava, jos mielipiteet jakautuvat kyselyn kohteiksi poimittujen joukossa samalla tavalla kuin kaikkien suomalaisten muodostamassa perusjoukossa. Kyselyn kohteiden valinta arpomalla on ainoa menetelma (satunnaisotanta), joka mahdollistaa edustavan pienoiskuvan saamisen. Arvonnan kaytto kyselyn kohteiden poiminnassa merkitsee sita, etta kyselyn tulokset ovat satunnaisia: Jos arvontaa toistettaisiin, kysely tuottaisi (suurella todennakoisyydella) joka kerran erilaiset tulokset, koska eri arvonnoissa kyselyyn poimittaisiin (suurella todennakoisyydella) eri henkilot. Jos kyselyn kohteiden poiminnassa on kaytetty satunnaisotantaa, kyselyn tuloksiin sisaltyvalle epavarmuudelle ja satunnaisuudelle voidaan muodostaa tilastollinen malli, joka mahdollistaa seka kyselyn tulosten yleistamisen etta yleistyksen luotettavuuden arvioinnin.
[14]
Suomessa Trafi ja Tilastokeskus muun muassa laativat ajoneuvo- ja ajokorttitilastoja. Ajoneuvoliikennerekisterin ajoneuvotietoja julkaistaan rekisterissa olevien ja liikennekaytossa olevien ajoneuvojen maarina. Tilastojen perusteella tehdaan erilaisia paatelmia esimerkiksi kansantalouden tilasta. Taloustilanteen ollessa huono ajoneuvoja ei hankita tai uusita yhta paljon kuin paremmassa taloustilanteessa.
[13]
Viralliset tilastot, vaestotieteen perusteet, indeksit ja kansantalouden tilinpito
[
muokkaa
|
muokkaa wikitekstia
]
Tilastokeskuksen ja muiden tahojen tuottamat viralliset tilastot kuvaavat maan taloudellisia ja sosiaalisia oloja, kuten seka tulonjakoa ja yritystoimintaa. Myos vaestonkehitysta kuten syntyvyytta, kuolevuutta ja muuttoliiketta seka tyomarkkinatilannetta kuvataan erilaisien tilastojen avulla. Tilastotieteen menetelmia sovelletaan myos erilaisten indeksien, kuten hinta-, kustannus- ja maaraindeksien, laskemisessa. Kansantalouden tilinpito on kansantalouden toimintaa kuvaava tilastojarjestelma, joka perustuu kansainvalisiin sopimuksiin. Sen avulla voidaan kuvata historiaa ja nykytilaa seka tehda erilaisia kansainvalisia vertailuja.
[15]
Vapaita
tilasto-ohjelmistoja:
Kaupallisia tilasto-ohjelmistoja:
- ↑
Kielitoimiston sanakirja
. Kotimaisten kielten tutkimuskeskuksen julkaisuja 132. Internet-versio MOT Kielitoimiston sanakirja 1.0. Helsinki: Kotimaisten kielten tutkimuskeskus ja Kielikone Oy, 2004.
ISBN 952-5446-11-5
.
- ↑
http://www.stat.fi/org/tilastokeskus/historia.html
- ↑
http://www.stat.fi/org/index.html
- ↑
http://www.suomenpankki.fi/fi/tilastot/Pages/default.aspx
- ↑
a
b
c
d
e
Moore D. S., McCabe G. P., Craig B. A.:
Introduction to the Practice of Statistics
. 6:s painos. New York: W. H. Freeman and Company, 2009.
ISBN 1-4292-1621-2
.
- ↑
a
b
c
d
Pahkinen E.:
Kyselytutkimusten otantamenetelmat ja aineistoanalyysi
. Jyvaskyla: Jyvaskyla University Printing House, 2012.
ISBN 978-951-39-4687-6
.
- ↑
a
b
c
Pawitan Y.:
In All Likelihood: Statistical Modelling and Inference Using Likelihood
. New York: Oxford University Press, 2001.
ISBN 978-0-19-850765-9
.
- ↑
Gelman A., Carlin J. B., Stern H. S., Rubin D. B.:
Bayesian Data Analysis
. 2:n painos. Chapman & Hall/CRC, 2004.
ISBN 1-58488-388-X
.
- ↑
Lunn D., Jackson C., Best N., Thomas A., Spiegelhalter D.:
The BUGS Book: A Practical Introduction to Bayesian Analysis
. Chapman & Hall/CRC, 2013.
ISBN 978-1-58488-849-9
.
- ↑
a
b
Davison A. C.: ”4”,
Statistical Models
. Cambridge: Cambridge University Press, 2003.
ISBN 0-521-77339-3
.
- ↑
Holland P. W.: Statistics and Causal Inference.
Journal of the American Statistical Association
, Joulukuu 1986, nro 81, s. 945?960. American Statistical Association.
Artikkelin verkkoversio
.
- ↑
Pearl J.: ”Luvut 2-3”,
Causality: models, reasoning, and inference
. New York: Cambridge University Press, 2000.
ISBN 0-521-77362-8
.
- ↑
a
b
Tilastotieteen sovelluksia
(PDF)
koti.mbnet.fi
.
Arkistoitu
3.5.2015. Viitattu 13.5.2014.
- ↑
a
b
Johdatus todennakoisyyslaskentaan ja tilastotieteeseen. Tilastotiede tieteenalana.
(PDF)
2004. Aalto-yliopisto..
Arkistoitu
13.5.2014. Viitattu 13.5.2014.
- ↑
Tilastokoulu
(PDF)
2014. Tilastokeskus.
- Gronroos, Matti:
Johdatus tilastotieteeseen: Kuvailu, mallit ja paattely
. Helsinki: Finn Lectura, 2003.
ISBN 951-792-148-9
.
- Heikkila, Juha:
Tilastotieteen ABC-kirja. 1, Kuvailevaa tilastotiedetta
. Helsinki: Yliopistopaino, 1993.
ISBN 951-570-184-8
.
- Heikkila, Tarja:
Tilastollinen tutkimus
. 7. uudistettu painos. Helsinki: Edita, 2008.
ISBN 978-951-37-4812-8
.
- Holopainen, Martti & Pulkkinen, Pekka:
Tilastolliset menetelmat
. Kuvitus: Krista Partti. 5. uudistettu painos. Porvoo Helsinki: WSOY Oppimateriaalit, 2008.
ISBN 978-951-0-33198-9
.
- Valli, Raine:
Johdatus tilastolliseen tutkimukseen
. Opetus 2000. Jyvaskyla: PS-kustannus, 2001.
ISBN 952-451-032-4
.
- Vasama, Pyry-Matti; Vartia, Yrjo:
Johdatus tilastotieteeseen, osa I
. Hameenlinna: Karisto, 1972.
ISBN 951-662-015-9
.
- Vasama, Pyry-Matti; Vartia, Yrjo:
Johdatus tilastotieteeseen, osa II
. Helsinki: Kyriiri, 1973.
ISBN 951-662-040-X
.
 Wikibooks
Wikibooks
 Commons
Commons