Бинарни систем

С Википеди?е, слободне енциклопеди?е
(преусмерено са Binary numeral system )

Бинарни систем ?е бро?чани систем у коме се запис састо?и само од цифара 0 и 1. Ово ?е позициони бро?чани систем , са основом 2. Сваки бро? се може представити као збир експонената дво?ке. Због ?едноставности примене у електронским колима, бинарни систем користе практично сви модерни рачунари .

Концепт бинарног система омогу?ен ?е тек са уво?е?ем концепта нуле у систему арапских цифара .

Пример бинарног записа: 101 2 = 1·2 2 + 0·2 1 + 1·2 0 , 101 у бинарном систему ?е еквивалент бро?у 5 у декадном систему.

Истори?а [ уреди | уреди извор ]

Египат [ уреди | уреди извор ]

Види ?ош: Староегипатска математика
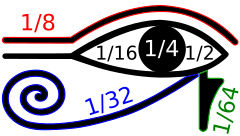Аритметичке вредности за ко?е се сматра да су представ?ене деловима Хорусовог ока

Писци старог Египта користили су два различита система за сво?е разломке, египатске разломке (ко?и нису повезани са бинарним бро?евним системом) и разломке Хорусовог ока (тако назване ?ер многи историчари математике веру?у да би симболи ко?и се користе за ова? систем могли бити распоре?ени тако да формира?у око Хоруса , иако ?е то спорно). [1] Разломци Хорусовог ока су бинарни систем нумериса?а за разломке количине зрна, течности или других мера, у ко?има се разломак хеката изражава као збир бинарних разломака 1/2, 1/4, 1/8, 1 /16, 1/32 и 1/64. Рани облици овог система могу се на?и у документима из Пете египатске династи?е , отприлике 2400. године пре нове ере, а ?егова потпуно разви?ена хи?ероглифска форма датира из Деветнаесте династи?е Египта , отприлике 1200. године п. н. е. [2]

Метода кориш?ена за староегипатско множе?е ?е тако?е блиско повезана са бинарним бро?евима. У ово? методи, множе?е ?едног бро?а са секундом се изводи низом корака у ко?има се вредност (у почетку први од два бро?а) или удвостручу?е или ?о? се вра?а први бро?; редослед ко?им се ови кораци треба?у извршити ?е дат бинарним приказом другог бро?а. Ова? метод се може видети у употреби, на пример, у Ра?ндовом математичком папирусу , ко?и датира од око 1650. године п. н. е. [3]

Кина [ уреди | уреди извор ]

Даоистичка Багуа

?и ?инг датира из 9. века п. н. е. у Кини. [4] Бинарни запис у ?и ?ингу се користи за тумаче?е ?егове технике квартарног прорица?а . [5]

То ?е било засновано на таоистичко? дуалности ?ина и ?анга . [6] Осам триграма (Багуа) и скуп од 64 хексаграма (?шездесет четири“ гуа), аналогни тробитним и шестобитним бинарним бро?евима, били су у употреби барем ?ош у династи?и ?оу у древно? Кини. [4]

Научник из династи?е Сонг Шао ?онг (1011?1077) преуредио ?е хексаграме у формат ко?и подсе?а на модерне бинарне бро?еве, иако ни?е намеравао да се ?егов распоред користи математички. [5] Гледа?е на?ма?е знача?ног бита на врху по?единачних хексаграма у Шао ?онговом квадрату [7] и чита?е дуж редова било од до?ег десног ка гор?ем левом углу са пуним лини?ама као 0 и испрекиданим лини?ама као 1 или од врха лево до доле десно са пуним лини?ама као 1 и испрекиданим лини?ама као 0 хексаграми се могу тумачити као низ од 0 до 63. [8]

Инди?а [ уреди | уреди извор ]

Инди?ски научник Пингала (око 2. века п. н. е.) развио ?е бинарни систем за описива?е метрике . [9] [10] Он ?е користио бинарне бро?еве у облику кратких и дугих слогова (пото?и ?еднаки дужини са два кратка слога), чине?и га сличним Морзеовом коду . [11] [12] Они су били познати као лагу (лаки) и гуру (тешки) слогови.

Пингалин хиндуистички класик под називом Чандахсастра (8.23) опису?е формира?е матрице како би се сваком метру дала ?единствена вредност. ?Чандахсастра“ се дословно преводи као наука о метрима на санскриту. Бинарне репрезентаци?е у Пингалином систему се пове?ава?у удесно, а не улево као у бинарним бро?евима модерне позиционе нотаци?е . [11] [13] У Пингалином систему бро?еви почи?у од бро?а ?едан, а не од нуле. Четири кратка слога ?0000” ?е први образац и одговара вредности ?едан. Бро?чана вредност се доби?а тако што се збиру вредности места дода ?едан. [14]

Друге културе [ уреди | уреди извор ]

Становници острва Мангарева у Француско? Полинези?и користили су хибридни бинарно- децимални систем пре 1450. године. [15] Прорезани буб?еви са бинарним тоновима се користе за кодира?е порука широм Африке и Ази?е. [6] Скупови бинарних комбинаци?а сличних ?и ?ингу су тако?е кориш?ени у традиционалним афричким системима прорица?а као што ?е Ифа , као и у сред?овековно? западно? геоманци?и .

Западни претходници Ла?бница [ уреди | уреди извор ]

У касном 13. веку Рамон Лул ?е имао амбици?у да об?асни сву мудрост у свако? грани ?удског зна?а тог времена. У ту сврху ?е развио општи метод или 'Ars generalis' заснован на бинарним комбинаци?ама низа ?едноставних основних принципа или категори?а, ко?и се сматра претходником рачунарске науке и вештачке интелигенци?е. [16]

Године 1605, Франсис Бе?кон ?е расправ?ао о систему у коме се слова абецеде могу свести на секвенце бинарних цифара, ко?е би потом могле бити кодиране као ?едва вид?иве вари?аци?е у фонту у било ком насумичном тексту. [17] Он ?е напоменуо да ?е важно за општу теори?у бинарног кодира?а, да се ова? метод може користити са било ко?им об?ектом: ?под условом да ти об?екти могу да има?у само двоструку разлику; као код звона, преко труба, помо?у светла и бак?и, према извешта?у мускета, и било каквих инструмената сличне природе“. [17] (Погледа?те Бе?конову шифру.)

?он Непер ?е 1617. описао систем ко?и ?е назвао локаци?ском аритметиком за обав?а?е бинарних прорачуна користе?и непозициону репрезентаци?у словима. Томас Хериот ?е истраживао неколико система позиционог нумериса?а, ук?учу?у?и бинарни, али ни?е об?авио сво?е резултате; прона?ени су касни?е ме?у ?еговим папирима. [18] Вероватно ?е прва публикаци?а система у Европи била рад Хуана Карамуела и Лобковица , 1700. године. [19]

Операци?е [ уреди | уреди извор ]

  • сабира?е:

 11001+

 01111=

101000

(25+15)=40

  • одузима?е:

101000-

 01111=

 11001

(40-15)=25

Примена [ уреди | уреди извор ]

Бинарни бро?чани систем ?е сво?у главну примену нашао у рачунарству. Велика ве?ина модерних рачунара користи бинарну логику - то ?ест податке запису?е и интерпретира у облику нула и ?единица .

Записива?е бро?ева у бинарном систему [ уреди | уреди извор ]

Да би се бро? превео из декадног система у бинарни, потребно ?е извршити ?едноставан поступак де?е?ем бро?ем 2. Ако желимо да напишемо бро? 13 у бинарном систему, треба да изведемо следе?и поступак: На?пре ?емо поделити бро? 13 бро?ем 2:

13:2=6 остатак 1

Остатак ?емо записати са стране(1), а количник(6) наставити да делимо:

6:2=3 остатак 0

Остатак ?емо записати са стране(0), а количник(3) наставити да делимо:

3:2=1 остатак 1

Остатак ?емо записати са стране(1), а количник(1) наставити да делимо:

1:2=0 остатак 1

Затим ?емо записати све остатке супротним редом од оног ко?им смо их доби?али(одоздо ка горе):

1101

И добили смо бро? 13 у бинарном систему, т? записаног само са две цифре.

Сваки бро? се претвара из декадног у бинарни систем бро?ева на исти начин, т?. де?е?ем и писа?ем остатака од кра??ег ка почетном, с тим што кра??и количник мора бити нула, а самим тим и кра??и остатак 1.

Бро?еви се могу записати и у другим позиционим системима бро?ева тако?е де?е?ем оним бро?ем ко?и одговара бро?у цифара у том систему (бинарни има 2 цифре па се бро?еви деле бро?ем 2) и записива?ем остатака.

Види ?ош [ уреди | уреди извор ]

Референце [ уреди | уреди извор ]

  1. ^ Robson, Eleanor ; Stedall, Jacqueline , ур. (2009), ?Myth No. 2: the Horus eye fractions”, The Oxford Handbook of the History of Mathematics , Oxford University Press, стр. 790, ISBN   9780199213122  
  2. ^ Chrisomalis, Stephen (2010), Numerical Notation: A Comparative History , Cambridge University Press, стр. 42?43, ISBN   9780521878180   .
  3. ^ Rudman, Peter Strom (2007), How Mathematics Happened: The First 50,000 Years , Prometheus Books, стр. 135?136, ISBN   9781615921768   .
  4. ^ а б Edward Hacker; Steve Moore; Lorraine Patsco (2002). I Ching: An Annotated Bibliography . Routledge. стр. 13. ISBN   978-0-415-93969-0 .  
  5. ^ а б Redmond & Hon (2014) , стр. 227.
  6. ^ а б Jonathan Shectman (2003). Groundbreaking Scientific Experiments, Inventions, and Discoveries of the 18th Century . Greenwood Publishing. стр. 29. ISBN   978-0-313-32015-6 .  
  7. ^ Shao Yong's square
  8. ^ Zhonglian, Shi; Wenzhao, Li; Poser, Hans (2000). Leibniz' Binary System and Shao Yong's "Xiantian Tu in :Das Neueste uber China: G.W. Leibnizens Novissima Sinica von 1697 : Internationales Symposium, Berlin 4. bis 7. Oktober 1997 . Stuttgart: Franz Steiner Verlag. стр. 165?170. ISBN   3515074481 .  
  9. ^ Sanchez, Julio; Canton, Maria P. (2007). Microcontroller programming: the microchip PIC . Boca Raton, Florida: CRC Press. стр.  37 . ISBN   978-0-8493-7189-9 .  
  10. ^ W. S. Anglin and J. Lambek, The Heritage of Thales , Springer, (1995) ISBN 0-387-94544-X
  11. ^ а б Binary Numbers in Ancient India
  12. ^ Math for Poets and Drummers Архивирано 16 ?ун 2012 на са?ту Wayback Machine (pdf, 145KB)
  13. ^ Stakhov, Alexey ; Olsen, Scott Anthony (2009). The mathematics of harmony: from Euclid to contemporary mathematics and computer science . ISBN   978-981-277-582-5 .  
  14. ^ B. van Nooten, "Binary Numbers in Indian Antiquity", Journal of Indian Studies, Volume 21, 1993, pp. 31-50
  15. ^ Bender, Andrea; Beller, Sieghard (16. 12. 2013). ?Mangarevan invention of binary steps for easier calculation” . Proceedings of the National Academy of Sciences . 111 (4): 1322?1327. PMC   3910603   Слободан приступ. PMID   24344278 . doi : 10.1073/pnas.1309160110   Слободан приступ.  
  16. ^ (see Bonner 2007 [1] Архивирано 3 април 2014 на са?ту Wayback Machine , Fidora et al. 2011 [2] Архивирано на са?ту Wayback Machine (8. април 2019))
  17. ^ а б Bacon, Francis (1605). ?The Advancement of Learning” . London. стр. Chapter 1.  
  18. ^ Shirley, John W. (1951). ?Binary numeration before Leibniz” . American Journal of Physics . 19 (8): 452?454. Bibcode : 1951AmJPh..19..452S . doi : 10.1119/1.1933042 .  
  19. ^ Ineichen, R. (2008). ?Leibniz, Caramuel, Harriot und das Dualsystem” (PDF) . Mitteilungen der deutschen Mathematiker-Vereinigung (на ?езику: немачки). 16 (1): 12?15. S2CID   179000299 . doi : 10.1515/dmvm-2008-0009 .  

Литература [ уреди | уреди извор ]

  • Sanchez, Julio; Canton, Maria P. (2007). Microcontroller programming: the microchip PIC . Boca Raton, FL: CRC Press. стр. 37. ISBN   978-0-8493-7189-9 .  
  • Redmond, Geoffrey; Hon, Tze-Ki (2014). Teaching the I Ching . Oxford University Press. ISBN   978-0-19-976681-9 .  
  • Boyer, Carl B. 1968. History of Mathematics . John Wiley. Reprint Princeton U. Press (1985).
  • Chace, Arnold Buffum. 1927?1929. The Rhind Mathematical Papyrus: Free Translation and Commentary with Selected Photographs, Translations, Transliterations and Literal Translations . 2 vols. Classics in Mathematics Education 8. Oberlin: Mathematical Association of America. (Reprinted Reston: National Council of Teachers of Mathematics, 1979). ISBN 0-87353-133-7
  • Clagett, Marshall. 1999. Ancient Egyptian Science: A Source Book . Volume 3: Ancient Egyptian Mathematics . Memoirs of the American Philosophical Society 232. Philadelphia: American Philosophical Society. ISBN 0-87169-232-5
  • Couchoud, Sylvia. 1993. Mathematiques egyptiennes: Recherches sur les connaissances mathematiques de l'Egypte pharaonique . Paris: Editions Le Leopard d'Or
  • Daressy, G. "Ostraca," Cairo Museo des Antiquities Egyptiennes Catalogue General Ostraca hieraques , vol 1901, number 25001-25385.
  • Gillings, Richard J. 1972. Mathematics in the Time of the Pharaohs . MIT Press. (Dover reprints available).
  • Imhausen, Annette . 2003. "Agyptische Algorithmen". Wiesbaden: Harrassowitz
  • Johnson, G., Sriraman, B., Saltztstein. 2012. "Where are the plans? A socio-critical and architectural survey of early Egyptian mathematics"| In Bharath Sriraman , Editor. Crossroads in the History of Mathematics and Mathematics Education . The Montana Mathematics Enthusiast Monographs in Mathematics Education 12, Information Age Publishing, Inc., Charlotte, NC
  • Neugebauer, Otto (1969) [1957]. The Exact Sciences in Antiquity (2 изд.). Dover Publications . ISBN   978-0-486-22332-2 . PMID   14884919 .  
  • Peet, Thomas Eric. 1923. The Rhind Mathematical Papyrus, British Museum 10057 and 10058 . London: The University Press of Liverpool limited and Hodder & Stoughton limited
  • Reimer, David (2014). Count Like an Egyptian: A Hands-on Introduction to Ancient Mathematics . Princeton, NJ: Princeton University Press . ISBN   978-0-691-16012-2 .  
  • Robins, R. Gay. 1995. "Mathematics, Astronomy, and Calendars in Pharaonic Egypt". In Civilizations of the Ancient Near East , edited by Jack M. Sasson, John R. Baines, Gary Beckman, and Karen S. Rubinson. Vol. 3 of 4 vols. New York: Charles Schribner's Sons. (Reprinted Peabody: Hendrickson Publishers, 2000). 1799?1813
  • Robins, R. Gay, and Charles C. D. Shute. 1987. The Rhind Mathematical Papyrus: An Ancient Egyptian Text . London: British Museum Publications Limited. ISBN 0-7141-0944-4
  • Sarton, George. 1927. Introduction to the History of Science , Vol 1. Willians & Williams.
  • Strudwick, Nigel G., and Ronald J. Leprohon. 2005. Texts from the Pyramid Age . Brill Academic Publishers. ISBN 90-04-13048-9 .
  • Struve, Vasilij Vasil'evi?, and Boris Aleksandrovi? Turaev. 1930. Mathematischer Papyrus des Staatlichen Museums der Schonen Kunste in Moskau . Quellen und Studien zur Geschichte der Mathematik; Abteilung A: Quellen 1. Berlin: J. Springer
  • Van der Waerden, B.L. 1961. Science Awakening". Oxford University Press.
  • Vymazalova, Hana. 2002. Wooden Tablets from Cairo.... , Archiv Orientalni, Vol 1, pages 27?42.
  • Wirsching, Armin. 2009. Die Pyramiden von Giza ? Mathematik in Stein gebaut . (2 ed) Books on Demand. ISBN 978-3-8370-2355-8 .

Спо?аш?е везе [ уреди | уреди извор ]

Бинарни систем на Викимеди?ино? остави .
Преузето из ? https://sr.wikipedia.org/w/index.php?title=Бинарни_систем&oldid=27549290 ”