| Calculo
|
|---|
|
|
|
|
Calculo integral
Definicoes
Integracao por
|
|
|
|
|
|
|
|
|
|
O
calculo infinitesimal
, tambem conhecido como
calculo diferencial e integral
ou simplesmente
calculo
, e um ramo importante da
matematica
, desenvolvido a partir da
Algebra
e da
Geometria
, que se dedica ao estudo de taxas de variacao de grandezas (como a inclinacao de uma reta) e a acumulacao de quantidades (como a
area
debaixo de uma curva ou o
volume
de um solido). Onde ha movimento ou crescimento em que forcas variaveis agem produzindo aceleracao, o calculo e a matematica a ser empregada. Foi criado como uma ferramenta auxiliar em varias areas das ciencias exatas. Desenvolvido simultaneamente por
Gottfried Wilhelm Leibniz
(
1646
-
1716
) e por
Isaac Newton
(
1643
-
1727
), em trabalhos independentes.
[
1
]
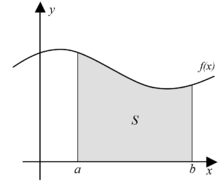 O calculo permite calcular a area da regiao assinalada.
O calculo permite calcular a area da regiao assinalada.
O calculo tem inicialmente tres "operacoes-base", ou seja, possui areas iniciais como o calculo de
limites
, o calculo de
derivadas
de
funcoes
e a
integral
de diferenciais. Com o advento do
Teorema Fundamental do Calculo
, estabeleceu-se uma conexao entre os dois ramos do calculo: o
Calculo Diferencial
e o
Calculo Integral
. O calculo diferencial surgiu do problema da
tangente
, enquanto o calculo integral surgiu de um problema aparentemente nao relacionado, o problema da area.
O professor de Isaac Newton em
Cambridge
,
Isaac Barrow
, descobriu que esses dois problemas estao de fato estritamente relacionados, ao perceber que a derivacao e a integracao sao processos inversos. Foram Leibniz e Newton que exploraram essa relacao e a utilizaram para transformar o calculo em um metodo matematico sistematico. Particularmente ambos viram que o Teorema Fundamental os capacitou a calcular areas e integrais muito mais facilmente, sem que fosse necessario calcula-las como limites de soma (metodo descrito pelo matematico
Riemann
, pupilo de
Gauss
). A integral indefinida tambem pode ser chamada de antiderivada, uma vez que e um processo que inverte a derivada de funcoes. Ja a integral definida, inicialmente definida como
Soma de Riemann
, estabelece limites de integracao, ou seja, e um processo estabelecido entre dois intervalos bem definidos, dai o nome integral definida.
[
2
]
O calculo diferencial e o calculo integral auxiliam em varios conceitos e definicoes na matematica,
quimica
,
fisica classica
,
fisica moderna
e
economia
. O estudante de calculo deve ter um conhecimento em certas areas da matematica, como funcoes (modular, exponencial, logaritmica, par, impar, afim e segundo grau, por exemplo),
trigonometria
, polinomios, geometria plana, espacial e analitica, pois sao a base do calculo.
A historia do calculo encaixa-se em varios periodos distintos, de forma notavel nas eras
antiga
,
medieval
e
moderna
.
 De acordo com
Gauss
,
Arquimedes
, o maior matematico da antiguidade, ja apresentava ideias relacionadas ao Calculo dois seculos antes de Cristo.
De acordo com
Gauss
,
Arquimedes
, o maior matematico da antiguidade, ja apresentava ideias relacionadas ao Calculo dois seculos antes de Cristo.
Na
Antiguidade
, foram introduzidas algumas ideias do calculo integral, embora nao tenha havido um desenvolvimento dessas ideias de forma
rigorosa
e sistematica. A funcao basica do calculo integral, a de calcular volumes e areas, pode ser remontada ao
Papiro Egipcio de Moscou
(
1850 a.C.
), no qual um egipcio trabalhou o volume de um
frustum
piramidal
. O calculo integral tambem pode ser utilizado para rastreamento e gravacao do movimento do sol, da lua e dos planetas. Os antigos
astronomos babilonios
(
1800
-
1600 a.C.
) empregaram metodos geometricos sofisticados que prenunciam o desenvolvimento do calculo para prever as posicoes dos corpos celestes.
[
3
]
[
4
]
Eudoxo de Cnido, ou Eudoxus,
(
408
-
355 a.C.
) usou o
metodo da exaustao
para calcular areas e volumes.
Arquimedes
(
287
-
212 a.C.
) levou essa ideia alem, inventando a
heuristica
, que se aproxima do calculo integral. O metodo da exaustao foi redescoberto na
China
por Liu Hui no
seculo III
, que o usou para encontrar a area do
circulo
. O metodo tambem foi usado por Zu Chongzhi
seculo V
, para achar o volume de uma
esfera
.
Na
Idade Media
, o matematico indiano
Aryabhata
usou a nocao infinitesimal em
499 d.C.
expressando-a em um problema de
astronomia
na forma de uma
equacao diferencial
basica. Essa equacao levou
Bh?skara II
no
seculo XII
a desenvolver uma derivada prematura representando uma mudanca infinitesimal, e ele desenvolveu tambem o que seria uma forma primitiva do "Teorema de Rolle".
No seculo XII, o matematico persa
Sharaf al-Din al-Tusi
descobriu a derivada de
polinomios
cubicos, um resultado importante no calculo diferencial. No
seculo XIV
,
Madhava de Sangamagrama
, juntamente com outros matematicos-astronomos da Escola Kerala de Astronomia e Matematica, descreveu casos especiais da
Serie de Taylor
, que no texto sao tratadas como Yuktibhasa.
 Sir
Isaac Newton
aplicou o calculo as suas
leis do movimento
e a outros conceitos matematicos-fisicos.
Sir
Isaac Newton
aplicou o calculo as suas
leis do movimento
e a outros conceitos matematicos-fisicos.
Na
Idade Moderna
, descobertas independentes no calculo foram feitas no inicio do
seculo XVII
no
Japao
por matematicos como Seki Kowa, que expandiu o metodo de exaustao. Na
Europa
, a segunda metade do seculo XVII foi uma epoca de grandes inovacoes. O Calculo abriu novas oportunidades na fisica-matematica de resolver problemas muito antigos que ate entao nao haviam sido solucionados. Muitos matematicos contribuiram para essas descobertas, notavelmente
John Wallis
e
Isaac Barrow
.
James Gregory
proveu um caso especial do segundo teorema fundamental do calculo em
1668
.
Coube a
Gottfried Wilhelm Leibniz
e a
Isaac Newton
recolher essas ideias e junta-las em um corpo teorico que viria a constituir o calculo. A ambos e atribuida a simultanea e independente invencao do calculo. Leibnitz foi originalmente acusado de plagiar os trabalhos nao publicados de Isaac Newton; hoje, porem, e considerado o inventor do calculo, juntamente com Newton. Historicamente Newton foi o primeiro a aplicar o calculo a fisica ao passo que Leibniz desenvolveu a notacao utilizada ate os dias de hoje, a
notacao de Leibniz
. O argumento historico para conferir aos dois a invencao do calculo e que ambos chegaram de maneiras distintas ao teorema fundamental do calculo.
 Gottfried Wilhelm Leibniz
: o inventor do calculo, juntamente com Newton.
Gottfried Wilhelm Leibniz
: o inventor do calculo, juntamente com Newton.
Quando Newton e Leibniz publicaram seus resultados, houve uma grande controversia de qual matematico (e portanto que pais:
Inglaterra
ou
Alemanha
) merecia o credito. Newton derivou seus resultados primeiro, mas Leibniz publicou primeiro. Newton argumentou que Leibniz roubou ideias de seus escritos nao publicados, que Newton a epoca compartilhara com alguns poucos membros da Sociedade Real. Esta controversia dividiu os matematicos ingleses dos matematicos alemaes por muitos anos. Um exame cuidadoso dos escritos de Leibniz e Newton mostra que ambos chegaram a seus resultados independentemente, com Leibniz iniciando com integracao e Newton com diferenciacao. Nos dias de hoje tem-se que Newton e Leibniz descobriram o calculo independentemente. Leibniz, porem, foi quem deu o nome calculo a nova disciplina, Newton a chamara de "A ciencia dos fluxos".
Desde o tempo de Leibniz e Newton, muitos matematicos contribuiram para o continuo desenvolvimento do calculo.
 Maria Gaetana Agnesi
Maria Gaetana Agnesi
Na
Idade Contemporanea
, ja no
seculo XIX
, o calculo foi abordado de uma forma muito mais rigorosa. Foi tambem durante este periodo que ideias do calculo foram generalizadas ao espaco
euclidiano
e ao plano complexo.
Lebesgue
mais tarde generalizou a nocao de integral. Sobressairam matematicos como
Cauchy
,
Riemann
,
Weierstrass
e
Maria Gaetana Agnesi
. Esta foi autora da primeira obra a unir as ideias de
Isaac Newton
e
Gottfried Wilhelm Leibniz
; escreveu tambem um dos primeiros livros sobre calculo diferencial e integral.
[
5
]
E dela tambem a autoria da chamada "
curva de Agnesi
".
O calculo e comumente utilizado pela manipulacao de quantidades muito pequenas. Historicamente, o primeiro metodo de utiliza-lo era pelas
infinitesimais
. Estes objetos podem ser tratados como numeros que sao, de alguma forma, "infinitamente pequenos". Na linha numerica, isso seria locais onde nao e zero, mas possui "zero" de distancia de zero. Nenhum numero diferente de zero e um infinitesimal, porque sua distancia de zero e positiva. Qualquer multiplo de um infinitesimal continua sendo um infinitesimal. Em outras palavras, infinitesimais nao satisfazem a propriedade arquimediana. Deste ponto de vista, o calculo e uma colecao de tecnicas para manipular infinitesimais. Tal pensamento foi ignorado no
seculo XIX
porque era muito dificil ter a nocao precisa de uma infinitesimal. Entretanto, o conceito foi reutilizado no
seculo XX
com a introducao da
analise nao padronizada
, a qual propiciou fundamentos solidos para a manipulacao de infinitesimais.
No seculo XIX, infinitesimais foram substituidos pelos
limites
. Limites descrevem o valor de uma funcao em um certo ponto
 a partir de valores da funcao em pontos proximos de
a partir de valores da funcao em pontos proximos de
 .
[
6
]
Um exemplo tradicional de interesse e o caso em que
.
[
6
]
Um exemplo tradicional de interesse e o caso em que
 e um
numero irracional
, como
e um
numero irracional
, como
 ou
ou
 , podendo ter seu valor decimal aproximado por numeros racionais proximos.
[
6
]
Outro caso e quando, ao tentar avaliar uma funcao
, podendo ter seu valor decimal aproximado por numeros racionais proximos.
[
6
]
Outro caso e quando, ao tentar avaliar uma funcao
 em
em
 , obtem-se uma
divisao por zero
, que e indefinida.
[
6
]
Eles capturam o comportamento numerico em baixa escala, como nas infinitesimais, mas utilizando numeros ordinarios. Deste ponto de vista, calculo e uma colecao de tecnicas para a manipulacao de certos limites. As infinitesimais foram substituidas por numeros muito pequenos, e o comportamento infinitamente pequeno da funcao e encontrado pelo limite de numeros cada vez menores. Limites sao faceis de serem colocados em fundacoes rigorosas e, por esse motivo, sao a abordagem padrao para o calculo.
, obtem-se uma
divisao por zero
, que e indefinida.
[
6
]
Eles capturam o comportamento numerico em baixa escala, como nas infinitesimais, mas utilizando numeros ordinarios. Deste ponto de vista, calculo e uma colecao de tecnicas para a manipulacao de certos limites. As infinitesimais foram substituidas por numeros muito pequenos, e o comportamento infinitamente pequeno da funcao e encontrado pelo limite de numeros cada vez menores. Limites sao faceis de serem colocados em fundacoes rigorosas e, por esse motivo, sao a abordagem padrao para o calculo.
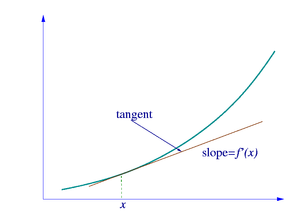 Reta
tangente
em (
x
,
f'
(
x
)).
Reta
tangente
em (
x
,
f'
(
x
)).
O calculo diferencial e o estudo da definicao, propriedade e aplicacoes da
derivada
ou deslocamento de um grafico. O processo de encontrar a derivada e chamado "diferenciacao". Em linguagem tecnica, a derivada e um operador linear, o qual forma uma nova funcao a partir da funcao original, em que cada ponto da nova funcao e o deslocamento da funcao original.
O conceito de derivada e fundamentalmente mais avancado do que os conceitos encontrados em
algebra
. Nessa materia, os estudantes aprendem sobre funcoes em que o numero de entrada gera um numero de saida. Por exemplo, se no dobro da funcao e inserido 3, entao a saida e 6, enquanto se a funcao e quadratica, e e inserido 3, entao a saida e 9. Mas na derivada, a entrada e uma funcao e a saida e outra funcao. Por exemplo, se na derivada e colocada uma funcao quadrada, entao a saida e o dobro de uma funcao, porque o dobro da funcao fornece o deslocamento da funcao quadratica em qualquer ponto dado da funcao.
Para entender a derivada, os estudantes precisam aprender a notacao matematica. Na notacao matematica, um simbolo comum para a derivada da funcao e um sinal de apostrofo chamado "linha". Entao a derivada de
f
e
f
' (f linha). Isso em notacao matematica seria escrito assim:

Se a funcao de entrada e o tempo, entao a derivada dessa funcao e a taxa em que a funcao e alterada.
Se a funcao e linear, ou seja, o grafico da funcao e uma linha reta, entao a funcao pode ser escrita como
y
=
m
x
+
b
, onde:

Isto da o valor exato para a variacao da linha reta. Se a funcao nao e uma linha reta, entao a variacao em
y
e dividida pela variacao em
x
, e nos precisamos do calculo para encontrar o valor exato em cada ponto da funcao. (Note-se que
y
e
f
(
x
) sao duas notacoes diferentes para a mesma coisa: a saida da funcao). Uma linha entre dois pontos em uma curva e chamado de reta secante. A variacao da reta secante pode ser expressada como:

onde as coordenadas do primeiro ponto e (x, f(x)) e h e a distancia horizontal entre os dois pontos.
Para determinar o deslocamento da curva, usam-se os
limites
:

Em um caso particular, nos encontramos o deslocamento da funcao quadratica no ponto em que a entrada e 3 e a saida e 9 (Ex.:
 entao
entao
 ).
).

O deslocamento da funcao quadratica no ponto (3, 9) e 6, isto e, ele cresce seis vezes mais rapido em y do que em x e esta indo para a direita.
O
Calculo Integral
e o estudo das definicoes, propriedades, e aplicacoes de dois conceitos relacionados, as
integrais indefinidas
e as
integrais definidas
. O processo de encontrar o valor de uma integral e chamado
integracao
. Em linguagem tecnica, o calculo integral estuda dois operadores lineares relacionados.
A
integral indefinida
e a
antiderivada
, o processo inverso da derivada. F e uma integral indefinida de
f
quando
f
e uma derivada de F. (O uso de letras maiusculas e minusculas para uma funcao e sua integral indefinida e comum em calculo.)
A
integral definida
insere uma funcao e extrai um numero, o qual fornece a area entre o grafico da funcao e o eixo do x. A definicao tecnica da integral definida e o limite da soma das areas dos retangulos, chamada Soma de Riemann.
Um exemplo motivacional e a distancia (
D
) viajada em um determinado tempo (
t
).

Se a velocidade (
V
) e constante, somente multiplicacao e necessaria, mas se a velocidade varia, entao precisamos de um metodo mais poderoso para encontrar a distancia. Um metodo e a aproximacao da distancia viajada pela divisao do tempo em muito mais intervalos de tempo, e entao multiplicando o tempo em cada intervalo por uma das velocidades naquele intervalo, e entao fazer uma Soma de Riemann das distancias aproximadas viajadas em cada intervalo. A ideia basica e que se somente um pequeno tempo passar, entao a velocidade vai permanecer praticamente a mesma. Entretanto, uma Soma de Riemann somente da uma aproximacao da distancia viajada. Nos precisamos pegar o limite de todas as Somas de Riemann para encontrar a distancia viajada exata.
 Integracao pode ser explicada neste exemplo, como a medida da area compreendida entre a curva
f
(
x
) e o eixo
x
, limitada pelos pontos
a
e
b
.
Integracao pode ser explicada neste exemplo, como a medida da area compreendida entre a curva
f
(
x
) e o eixo
x
, limitada pelos pontos
a
e
b
.
Se
f(x)
no diagrama da esquerda representa a velocidade variando de acordo com o tempo, a distancia viajada entre os tempos representados por
a
e
b
e a area da regiao escura
s
.
Para aproximar a area, um metodo intuitivo seria dividir em distancias entre
a
e
b
em um numero de segmentos iguais, a distancia de cada segmento representado pelo simbolo
?x
. Para cada segmento menor, nos podemos escolher um valor da funcao
f
(
x
). Chame o valor
h
. Entao a area do retangulo com a base
?x
e altura
h
da a distancia (tempo
?x
multiplicado pela velocidade
h
) viajado naquele segmento. Associado com cada segmento e o valor medio da funcao sobre ela,
f(x)
=h. A soma de todos os retangulos dados e uma aproximacao da area entre o eixo e a curva, o qual e uma aproximacao da distancia total viajada. Um valor menor para
?x
nos dara mais retangulos e, na maioria dos casos uma melhor aproximacao, mas para uma resposta exata nos precisamos fazer o limite em
?x
tender a zero.
O simbolo da integracao e
 um
S
alongado (que significa "soma"). A integral definida e escrita da forma:
um
S
alongado (que significa "soma"). A integral definida e escrita da forma:

e lida como "a integral de
a
ate
b
de
f
-de-
x
em relacao a
x
."
A integral indefinida, ou antiderivada, e escrita da forma:

Desde que a derivada da funcao
 e
e
 (onde
C
e qualquer constante), entao:
(onde
C
e qualquer constante), entao:

Seja um conjunto de pontos
A
, cujos membros sao os numeros em
 entao tomamos
entao tomamos
 e denominamo-la
variavel independente
, visto que, arbitrariamente, lhe podemos atribuir qualquer valor em
e denominamo-la
variavel independente
, visto que, arbitrariamente, lhe podemos atribuir qualquer valor em
 e portanto dizemos que:
e portanto dizemos que:
A
e o
dominio
da variavel
 [
7
]
[
7
]
Da mesma forma, admitamos um conjunto de pontos
B
, cujos membros sao numeros que sao obtidos unica e exclusivamente por um conjunto de regras matematicas
 , quando numeros arbitrarios em
A
lhe sao transferidos; visto que ha um unico valor assumido para cada valor arbitrario transferido a
, quando numeros arbitrarios em
A
lhe sao transferidos; visto que ha um unico valor assumido para cada valor arbitrario transferido a
 , dizemos que:
, dizemos que:
B
e
funcao
de
A
.
Sendo
B
obtido atraves das regras de

A
e
dominio
da funcao

Da mesma forma, como
B
e restrito aos valores definidos por
A
e as regras definidas por
 os seus elementos espelham estas condicoes, portanto, podemos dizer que:
os seus elementos espelham estas condicoes, portanto, podemos dizer que:
B
e
imagem
da funcao

Observe-se a expressao:
 Nota-se que, assim que sao atribuidos valores a
Nota-se que, assim que sao atribuidos valores a
 ela assumira valores invalidos, ou seja, de raizes quadradas de numeros negativos. Para sanar este problema, pode-se atribuir uma faixa de valores validos para o dominio de
ela assumira valores invalidos, ou seja, de raizes quadradas de numeros negativos. Para sanar este problema, pode-se atribuir uma faixa de valores validos para o dominio de
 o que resultara em:
o que resultara em:

Assim, tem-se um dominio restrito a valores iguais ou menores que 12. Portanto, incluindo-o, este extremo ao qual pertence o valor 12 e chamado de
extremo fechado
.
Tem-se uma situacao semelhante, porem com uma sutil diferenca, quando for necessario fazer:
 . Neste caso, e preciso restringir o valor 0 e todos os numeros abaixo dele, desta forma:
. Neste caso, e preciso restringir o valor 0 e todos os numeros abaixo dele, desta forma:

Pode-se atribuir apenas valores maiores que 0, uma vez que este valor nao pertence ao conjunto de numeros que podem ser atribuidos a variavel, o que se denomina de
extremo aberto
.
O conjunto de numeros
B
 dos quais
dos quais
 dependem do conjunto
A
dependem do conjunto
A
 de onde se obtem
de onde se obtem
 e se estabelece o par de numeros
e se estabelece o par de numeros
 ou simplesmente:
ou simplesmente:

Este e chamado de
par ordenado
.
Sendo tambem
 a representacao dos valores de
a representacao dos valores de
 entao pode-se afirmar que:
entao pode-se afirmar que:

Sendo
 o valor de
o valor de
 , quando definido pelas operacoes em
, quando definido pelas operacoes em

Faixas de valores que delimitam os dominios podem ser representados com desigualdades, como nos exemplos abaixo:

Porem, os extremos podem ser colocados em um par entre delimitadores de forma que, para os extremos fechados usa-se os delimitadores [ ou ]. Para os extremos abertos usa-se ( ou ), habilitando a identificar os extremos mais claramente. Assim, pode-se identificar os dominios do exemplo acima desta forma:

Tambem e comum usar colchetes invertidos para extremos abertos:
![{\displaystyle ]-2,4[;[-12,8[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86782294232542452314bef3fe6a71a4fb92e176)
Considere-se duas funcoes
f
e
g
; admitindo que as duas sao, intuitivamente, expressoes que se traduzem em valores, pode-se dizer que:




Sendo
D(f)
o dominio da funcao
f
e
D(g)
o dominio da funcao
g
, o dominio da funcao resultante das operacoes acima e sempre:

O teorema fundamental do calculo afirma que a diferenciacao e a integracao sao operacoes inversas. Mais precisamente, o teorema conecta os valores de antiderivadas ao valor de integrais definidas. Por ser usualmente mais facil computar uma antiderivada do que aplicar a definicao de uma integral definida, o teorema fundamental do calculo prove uma forma pratica de computar integrais definidas. Pode tambem ser interpretado como uma afirmacao precisa do fato que a diferenciacao e o inverso da integracao.
[
8
]
E afirmado pelo teorema fundamental do calculo que: Se uma funcao
f
e continua no intervalo [
a
,
b
] e se
F
e uma funcao cuja derivada e
f
no intervalo (
a
,
b
), entao

Alem disso, para cada x no intervalo (
a
,
b
) temos que

E, seu Corolario pode ser transcrito da seguinte forma:
Considere-se
f
uma
funcao continua
de valores reais definida em um intervalo fechado [
a
,
b
]. Se
F
e uma funcao tal que
 para todo
x
em [
a
,
b
]
para todo
x
em [
a
,
b
]
entao

e

Essa descoberta, realizada por
Newton
e
Leibniz
, que se basearam nos resultados de um trabalho anterior de
Isaac Barrow
, exerceu um papel chave na massiva proliferacao de resultados analiticos que se seguiram apos seus trabalhos ficarem conhecidos. O Teorema fundamental do calculo prove um metodo algebrico de computar muitas integrais definidas sem executar processos limite?simplesmente por encontrar formula para antiderivadas.
O calculo e usado em todos os ramos das
ciencias fisicas
, na
ciencia da computacao
,
estatistica
,
engenharia
,
economia
,
medicina
e em outras areas sempre que um problema possa ser
modelado matematicamente
e uma solucao
otima
e desejada, ele e um estudo mais profundo de
funcoes
.
A
Fisica
faz uso intensivo do calculo. Todos os conceitos na
mecanica classica
sao inter-relacionados pelo calculo. A
massa
de um objeto de
densidade
conhecida, o
momento de inercia
dos objetos, assim como a
energia
total de um objeto dentro de um sistema fechado podem ser encontrados usando o calculo. Nos sub-campos da
eletricidade
e
magnetismo
, o calculo pode ser usado para encontrar o
fluxo
total de campos eletromagneticos. Um exemplo mais historico do uso do calculo na fisica e a
segunda lei de Newton
que usa a expressao "taxa de variacao" que se refere a derivada:
A
taxa de variacao
do momento de um corpo e igual a forca resultante que age sobre o corpo e na mesma direcao.
Ate a expressao comum da segunda lei de
Newton
como Forca = Massa × Aceleracao envolve o calculo diferencial porque a
aceleracao
pode ser expressada como a derivada da velocidade. A teoria do
Eletromagnetismo
de Maxwell e a teoria da
relatividade geral
de
Einstein
tambem sao expressas na linguagem do calculo diferencial. A quimica tambem usa o calculo para determinar as variacoes na velocidade das reacoes e no
decaimento radioativo
.
O calculo pode ser usado em conjunto com outras disciplinas matematicas. Por exemplo, ele pode ser usado com a
algebra linear
para encontrar a reta que melhor representa um conjunto de pontos em um dominio.
Na esfera da
medicina
, o calculo pode ser usado para encontrar o angulo otimo na ramificacao dos vasos sanguineos para maximizar a circulacao, e ate mesmo determinar o tamanho maximo de moleculas que sao capazes de atravessar a membrana plasmatica em uma determinada situacao, normal ou induzida, em celulas.
Na
geometria analitica
, o estudo dos graficos de funcoes, o calculo e usado para encontrar pontos maximos e minimos, a inclinacao,
concavidade
e
pontos de inflexao
.Na
Engenharia civil
e usado para encontrar o
momento fletor
maximo de uma
viga
num ponto qualquer.
Na
Economia
o calculo permite a determinacao do lucro maximo fornecendo uma formula para calcular facilmente tanto o
custo marginal
quanto a
renda marginal
.
O calculo pode ser usado para encontrar solucoes aproximadas de
equacoes
, em metodos como o
metodo de Newton
,
iteracao de ponto fixo
e
aproximacao linear
. Por exemplo, naves espaciais usam uma variacao do
metodo de Euler
para aproximar
trajetorias
curvas em ambientes de queda livre.
Referencias
- Medeiros, Valeria Zuma (2005). Thomsom Pioneira, 1ª edicao.
Pre-Calculo
ISBN 8522104506
- Coelho, Flavio Ulhoa (2005). Saraiva, 1ª edicao.
Curso Basico de Calculo
ISBN 8502051202
- Mendelson, Elliot (2007). Bookman Companhia Editora, 2ª edicao.
Introducao ao Calculo
ISBN 8560031537
- Guidorizzi, Hamilton; LTC; 5ª edicao, 2001; 4 vols.
ISBN 8521612591
- Piskounov, Nikolai Semenovich
; Edicoes Lopes da Silva; 12ª edicao, 2002; 2 vols.
- Goldstein, Larry J./Schneider, David I. (2007); Hemus; 1ª edicao, volume unico.
Calculo e suas Aplicacoes
ISBN 8528905330
- Stewart, James (2002). Thomsom Pioneira, 5ª edicao, 2 vols.
Calculo
ISBN 8522106606
- Thomas, George B. (2012).
Calculo Volume 1
. Sao Paulo: Pearson Education do Brasil.
ISBN
9788581430867
- Anton, Howard A. (2007). Bookman Companhia Editora, 8ª edicao, 2 vols.
Calculo
ISBN 8560031804
- Barboni, Ayrton/Paulette, Walter (2007). LTC, 1ª edicao.
Fundamentos da Matematica: Calculo e Analise
ISBN 8521615469
- Ayres Jr., Frank/Mendelson, Elliot (2006), Bookman Companhia Editora, 4ª edicao.
Calculo
, col. Schaum
ISBN 856003109X
- Bradley, Gerald L./Hoffman, Laurence D. (2008). LTC, 9ª edicao.
Calculo:Um Curso Moderno e suas Aplicacoes
ISBN 8521616023
- Lopes, Helio/Malta, Iaci/Pesco, Sinesio (2002). Loyola, 1ª edicao, 2 vols.
Calculo a uma Variavel
ISBN 8515024403
- Hughes-Hallett, Deborah (2005). LTC, 2ª edicao.
Calculo Aplicado
ISBN 8521613970
- Larson, Ron/Edwards, Brruce (2005). LTC, 6ª edicao
Calculo com Aplicacoes
ISBN 8521614330
- Avila, Geraldo (2003). LTC, 7ª edicao, 3 vols.
Calculo das Funcoes de uma Variavel
ISBN 8521613709
- Hallett, Hughes (2004). LTC, 7ª edicao.
Calculo de uma Variavel
ISBN 8521613903
- Salas/Hille/Etgen (2005). LTC, 9ª edicao, 2 vols.
Calculo
ISBN 8521614594
- Apostol, Tom
(2004). Editora Reverte, 2ª edicao.
Calculo
, Vol. 1.
ISBN 8429150153
- Courant, R./John, F. Springer (1998)
Introduction to Calculus and Analysis
, Vol. 1.
ISBN 354065058X
- Spivak, M. Publish or Perish (2008)
Calculus
.
ISBN 0914098918
- Wrede, Robert C./Spiegel, Murray R. (2003). Bookman Companhia Editora, 2ª edicao
Calculo Avancado
ISBN 8536303476
- Hellmeister, Ana Catarina Pontone, organizadora. EDUSP, 2ª edicao (2006)
Calculo Integral Avancado
ISBN 8531403707
- Bortolossi, Humberto Jose (2002). Loyola, 1ª edicao
Calculo a Varias Variaveis: Uma Introducao a Teoria da Otimizacao
ISBN 851502442X
- Spivak, Michael (2003). Ciencia Moderna, 1ª edicao
Calculo em Variedades
ISBN 8573932252
 Wikilivros
Wikilivros
 Wikilivros
Wikilivros
 Wikilivros
Wikilivros
|
|---|
| Historia
| |
|---|
| Ramos correlacionados
| |
|---|
| Formalizacoes
| |
|---|
| Conceitos individuais
| |
|---|
| Pessoas
| |
|---|
| Fisica/Engenharia
| |
|---|
| Livros texto
| |
|---|
Areas da matematica
|
|---|
| Areas
| |
|---|
| Divisoes
| |
|---|