Eulerova formula , nazvana prema Leonhardu Euleru , prikazuje u podru?ju analize kompleksnih brojeva duboku povezanost trigonometrijskih funkcija s kompleksnim eksponencijalnim funkcijama . Eulerova formula ustanovljava da je za svaki realni broj   x ,

${\displaystyle e^{ix}=\cos x+i\sin x\!}$

gdje je e matemati?ka konstanta i baza prirodnih logaritama , i imaginarna jedinica, a sin i cos trigonometrijske funkcije s argumentom x datim u radijanima . Eulerova formula vrijedi i ako je x kompleksni broj te se ponekad ova formula navodi i u njezinom op?enitijem, kompleksnom obliku. Ova formula prema nekim autorima smatra se jednom od “najizuzetnijih formula na podru?ju cijele matematike”.

Njezin se dokaz mo?e na?i u obja?njenju Eulerovog identiteta .

Povijest [ uredi | uredi kod ]

Bernoulli je 1702. godine zapisao da je

${\displaystyle {\frac {dx}{1+x^{2}}}={\frac {1}{2}}\left({\frac {dx}{1-ix}}+{\frac {dx}{1+ix}}\right).}$

te da je

${\displaystyle \int {\frac {dx}{1+x}}=\ln(1+x),}$

Gore navedene jednakosti daju nam određeni uvid u pojam kompleksnih logaritmima. Bernoulli, međutim, nije ocijenio cjelinu. Njegovo dopisivanje s Eulerom (koji je također poznavao jednakost) pokazuje da nije naslutio dubinu matemati?ke pozadine. U međuvremenu je Roger Cotes 1714. godine otkrio da je

${\displaystyle \ln(\cos x+i\sin x)=ix\ }$

Međutim, Cotes nije uo?io ?injenicu da kompleksni logaritmi mogu imati beskona?no mnogo vrijednosti i to posljedi?no periodi?nosti trigonometrijskih funkcija. Upravo je Euler, negdje oko 1740. godine, obratio pa?nju na eksponencijalne funkcije umjesto logaritamskih i izveo formulu koja je nazvana njemu u ?ast. Formula

${\displaystyle e^{ix}=\cos x+i\sin x\,\!}$

je objavljena 1748. godine i Eulerov dokaz formule je zasnovan na jednakosti beskona?nih redova obiju strana izvoda. Nitko, međutim, u to doba nije uo?io geometrijsku interpretaciju formule, kao pogled na kompleksne brojeve predo?ene u kompleksnoj ravnini. Tu su vezu tek nekih pedesetak godina kasnije ustanovili neovisno jedan o drugome prvo Caspar Wessel pa Carl Friedrich Gauss .

Primjene u teoriji kompleksnih brojeva [ uredi | uredi kod ]

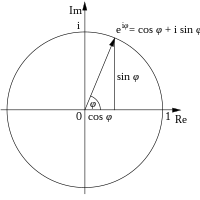
Eulerova formula mo?e se predo?iti na na?in da funkcija e ^ix rotira oko ishodi?ta kompleksne ravnine tijekom ?ega x poprima vrijednosti iz domene realnih brojeva. U tom smislu x je kut ?to ga ?ini du?ina, koja spaja ishodi?te koordinatnog sustava u kompleksnoj ravnini s odgovaraju?om to?kom na jedini?noj kru?nici, s pozitivnom realnom osi. Pri tome du?ina, u osnovi vektor u kompleksnoj ravnini, rotira smjerom suprotno od smjera kazaljki na satu, a veli?ina kuta iskazuje se u radijanima. Izvorni dokaz se zasniva na razvoju Taylorovih redova za eksponencijalnu funkciju e ^z te periodi?ke funkcije sin  x i cos  x , gdje je z kompleksni broj, a x realan broj. Isti dokaz pokazuje da formula vrijedi i ako je x bilo koji kompleksan broj.

Eulerova formula na jednostavan na?in omogu?ava prijelaz iz prikaza kompleksnog broja u kartezijanskim koordinatama u prikaz kompleksnog broja u polarnim koordinatama. Iskaz kompleksnog broja u polarnim koordinatama bitno pojednostavljuje slo?enije operacije s kompleksnim brojevima kao ?to su, na primjer, mno?enje i potenciranje, a iz razloga ?to se bilo koji kompleksan broj z = x  +  iy mo?e zapisati kao

${\displaystyle z=x+iy=|z|(\cos \phi +i\sin \phi )=|z|e^{i\phi }\,}$

${\displaystyle {\bar {z}}=x-iy=|z|(\cos \phi -i\sin \phi )=|z|e^{-i\phi }\,}$

gdje je

${\displaystyle x=\mathrm {Re} \{z\}\,}$ realni dio

${\displaystyle y=\mathrm {Im} \{z\}\,}$ imaginarni dio

${\displaystyle |z|={\sqrt {x^{2}+y^{2}}}}$ apsolutna vrijednost ili veli?ina od z

${\displaystyle \phi =\,}$ arctan( y , x ) zadan u radijanima.

Povezanost s trigonometrijom [ uredi | uredi kod ]

Eulerova formula iskazuje sna?nu povezanost između matemati?ke analize i trigonometrije te omogu?uje prikaz sin i cos funkcije u odgovaraju?em obliku eksponencijalnih funkcija.

${\displaystyle \cos x=\mathrm {Re} \{e^{ix}\}={e^{ix}+e^{-ix} \over 2}}$

${\displaystyle \sin x=\mathrm {Im} \{e^{ix}\}={e^{ix}-e^{-ix} \over 2i}.}$

Gornje jednad?be mogu se izvesti zbrajaju?i ili oduzimaju?i Eulerove formule

${\displaystyle e^{ix}=\cos x+i\sin x\;}$

${\displaystyle e^{-ix}=\cos(-x)+i\sin(-x)=\cos x-i\sin x\;}$

i rje?avaju?i ih po sin ili cos funkciji. Ove formule mogu ?ak poslu?iti kao definicije trigonometrijskih funkcija kompleksnog argumenta x . Naime, stavimo li x = iy , nalazimo da je

${\displaystyle \cos(iy)={e^{-y}+e^{y} \over 2}=\cosh(y)}$

${\displaystyle \sin(iy)={e^{-y}-e^{y} \over 2i}=-{1 \over i}{e^{y}-e^{-y} \over 2}=i\sinh(y).}$

Kompleksne eksponencijalne funkcije znatno pojednostavljuju trigonometriju jer je daleko lak?e ra?unati s njima nego sa sinusnim, odn. kosinusnim ekvivalentima. Jedan od na?ina je da se prikaz periodi?ke funkcije jednostavno prika?e pomo?u eksponencijalnom funkcijom. Na primjer

${\displaystyle {\begin{aligned}\cos x\cdot \cos y&={\frac {(e^{ix}+e^{-ix})}{2}}\cdot {\frac {(e^{iy}+e^{-iy})}{2}}\\&={\frac {1}{2}}\cdot {\frac {e^{i(x+y)}+e^{i(x-y)}+e^{i(-x+y)}+e^{i(-x-y)}}{2}}\\&={\frac {1}{2}}\left[\underbrace {\frac {e^{i(x+y)}+e^{-i(x+y)}}{2}} _{\cos(x+y)}+\underbrace {\frac {e^{i(x-y)}+e^{-i(x-y)}}{2}} _{\cos(x-y)}\right].\end{aligned}}}$

Druge primjene [ uredi | uredi kod ]

U elektrotehnici i drugim podru?jima, elektri?ni signali, odn. veli?ine koje se periodi?ki mijenjaju s vremenom ?esto se opisuju kao kombinacije sinusnih i kosinusnih funkcija ( Fourierova analiza ) te se kao takve izra?avaju u obliku eksponencijalnih funkcija s imaginarnim eksponentima, koriste?i upravo Eulerovu formulu. ?tovi?e, analiza elektri?nih krugova i mre?a mo?e uklju?iti upravo Eulerovu formulu i njezine derivate u svrhu prikaza faznih i amplitudnih odnosa struje i napona.