Hexaedro
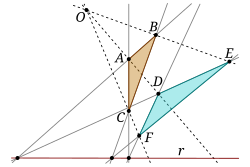Unha ilustracion do
teorema de Desargues
, un resultado importante nas xeometrias
euclidiana
e
proxectiva
.
A
xeometria
(do grego
γεωμετρ?α
; palabra composta de
γ?
,geo, "terra", e
μ?τρον
,metron, "medida") e a rama das
matematicas
concernente con cuestions de forma, tamano, posicion relativa de figuras, e coas propiedades do espazo. Os
matematicos
que traballan no campo da xeometria chamanse
xeometras
.
A
xeometria
desenvolveuse independentemente nun gran numero de civilizacions antigas como un corpo de conecemento practico relacionado con
lonxitudes
,
areas
e
volumes
, con elementos de ciencia matematica formal, polo menos a partir do
seculo VI a.C.
con
Tales de Mileto
. No
seculo III a.C.
,
Euclides
axiomatizou
a
xeometria
, este modelo conecido como
xeometria euclidiana
estivo vixente durante moitos seculos.
[
1
]
.
Arquimedes
ideou tecnicas enxenosas para calcular areas e volumes que anticipaban en moitos puntos o
calculo integral
moderno.
Durante o milenio e medio seguinte, a
astronomia
foi unha importante fonte de problemas xeometricos que contribuiron ao seu desenvolvemento, especialmente o establecemento da posicion das
estrelas
e os
planetas
na
esfera celeste
e a descricion das relacions entre os movementos dos corpos celestes. Tanto a xeometria como a astronomia formaban parte do
Quadrivium
do mundo clasico, catro das sete
artes liberais
consideradas esenciais para a formacion de cidadans libres.
A introducion das
coordenadas
por
Rene Descartes
e o desenvolvemento concorrente da
alxebra
, marcan un novo estadio da xeometria no que as figuras xeometricas, como as
curvas planas
, podian representarse agora dun xeito
analitico
, e dicir, con
funcions
e
ecuacions
. Isto xogou un papel fundamental no nacemento do
calculo infinitesimal
no
seculo XVII
. Ademais, a teoria da
perspectiva
mostrou que estaba mais relacionada coa xeometria que coas propiedades metricas das figuras, de feito, a perspectiva e a orixe da
xeometria proxectiva
. A disciplina da xeometria foi posteriormente enriquecida polo estudo da estrutura intrinseca dos obxectos xeometricos iniciado por
Euler
e
Gauss
e que levou a creacion da
topoloxia
e a
xeometria diferencial
.
No tempo de Euclides non estaba clara a distincion entre o espazo fisico e o espazo xeometrico. Desde o descubrimento no
seculo XIX
de
xeometrias non euclidianas
, o concepto de
espazo
sufriu transformacions radicais e xurdiu unha pregunta clave: cales son os espazos xeometricos que mellor se axustan ao espazo fisico? Coa irrupcion das matematicas formais no
seculo XX
, mesmo o concepto de
espazo
(e
punto
,
lina
,
plano
) perdeu o seu contido intuitivo, de xeito que hoxe en dia debese distinguir entre espazo fisico, espazos xeometricos (nos que os conceptos de
espazo
,
punto
etc. ainda conservan o seu significado intuitivo) e espazos abstractos. A xeometria contemporanea considera
variedades
, espazos que son considerabelmente mais abstractos cos familiares
espazos euclidianos
, aos que so se asemellan a pequenas escalas. Estes espazos deben ser provistos con estruturas adicionais que permitan falar de lonxitude. A xeometria moderna esta estreitamente relacionada coa
fisica
, exemplificada polos lazos existentes entre as
variedades pseudoriemannianas
e a
teoria xeral da relatividade
. Unha das mais novas teorias fisicas, a
teoria de cordas
, ten tamen unha esencia moi xeometrica.
Mentres que a natureza visual da xeometria faina inicialmente mais accesibel ca outras partes das matematicas, tales como a alxebra e a
teoria de numeros
, a linguaxe xeometrica usase tamen en contextos afastados da sua tradicional orixe euclidiana, como, por exemplo, na
xeometria fractal
e na
xeometria alxebrica
.
Demostracion
visual do
Teorema de Pitagoras
para o
triangulo
de lados 3, 4 e 5, tal como aparece no
Chou Pei Suan Ching
500?200 a.C.
O desenvolvemento da xeometria esta rexistrado durante mais de dous
milenios
. Sorprenden enormemente as diferentes percepcions do que e xeometria ao longo de todo este tempo.
A orixe da xeometria como unha ciencia practica ten que ver coa topografia, as medidas, areas e volumes. Entre os logros notabeis achanse formulas para calcular lonxitudes, areas e volumes, tales como o
teorema de Pitagoras
, a lonxitude da
circunferencia
, as areas dun
circulo
ou dun
triangulo
, os volumes dun
cilindro
, unha
esfera
ou unha
piramide
... Un metodo para calcular certas distancias inaccesibeis ou alturas baseado na
semellanza
de figuras xeometricas atribueselle a
Tales
. O desenvolvemento da
astronomia
levou ao nacemento da
trigonometria
(plana e esferica), xunto coas concorrentes tecnicas de contabilizacion,
Unha ilustracion do
postulado das paralelas de Euclides
.
Euclides
fixo unha aproximacion mais abstracta a xeometria nos seus
Elementos
, un dos libros mais influentes xamais escritos. Euclides introduciu certos
axiomas
, ou
postulados
, que expresan propiedades primarias ou autoevidentes de puntos, linas, e planos. Procedeu a deducir rigorosamente outras propiedades mediante o razoamento matematico. O aspecto caracteristico da aproximacion de Euclides a xeometria foi o seu rigor, e o seu metodo chegou a conecerse como xeometria
axiomatica
ou
sintetica
. A comezos do seculo XIX o descubrimento das xeometrias non euclidianas por
Gauss
,
Lobachevsky
,
Bolyai
, e outros levou a un renacemento do interese pola xeometria axiomatica, e no seculo XX
David Hilbert
empregou o razoamento axiomatico nun intento de dotar a xeometria duns fundamentos modernos.
Leccions de xeometria no
seculo XX
.
Os xeometras clasicos prestaban especial atencion a construcion de obxectos xeometricos definidos dalgunha outra forma. Os unicos instrumentos permitidos no mundo clasico eran o
compas
e a
regra
sen graduar. Amais, cada construcion tina que ser completada nun numero finito de pasos. Poren, fixose evidente nalguns destes problemas a dificultade ou imposibilidade da sua solucion, e acharonse enxenosas construcions usando parabolas e outras curvas, ademais de recursos mecanicos.
Os pitagoricos descubriron que os lados dun triangulo poden ter lonxitudes
inconmensurabeis
.
Na
antiga Grecia
os pitagoricos consideraron o papel dos
numeros
en xeometria. Poren, o descubrimento de lonxitudes
inconmensurabeis
, que contradician os puntos de vista filosoficos, fixo que abandonaran os numeros abstractos en favor das cantidades xeometricas concretas, como a lonxitude e a area de figuras. Os numeros foron reintroducidos na xeometria en forma de
coordenadas
por
Descartes
, quen se deu conta de que o estudo das formas xeometricas podia facilitarse pola sua representacion alxebrica. Posteriormente na sua honra nomeouse ao plano con coordenadas,
plano cartesiano
. A
xeometria analitica
aplica metodos da
alxebra
a cuestions xeometricas, relacionando frecuentemente
curvas
xeometricas e
ecuacions
alxebricas. Estas ideas xogaron un papel fundamental no desenvolvemento do
calculo infinitesimal
no
seculo XVII
e levaron ao descubrimento de moitas propiedades das curvas planas. A moderna
xeometria alxebrica
considera cuestions similares a un nivel moito mais abstracto.
Mesmo nos tempos antigos, os xeometras trataron cuestions de posicions relativas ou relacions espaciais de figuras e formas xeometricas. Alguns exemplos venen dados polas circunferencias inscritas e circunscritas aos
poligonos
, as rectas tanxentes e secantes as seccions conicas, as configuracions de
Pappus
e
Menelao
de puntos e rectas. Na Idade Media consideraronse cuestions deste tipo mais complicadas: Cal e o numero maximo de esferas que simultaneamente tocan a outra esfera do mesmo radio (
numero de osculacion
)? Cal e o empaquetado mais denso de esferas de igual tamano que se pode conseguir no espazo (
conxectura de Kepler
)? A maioria destas cuestions tratan con formas xeometricas "rixidas", como linas ou esferas. As xeometrias
proxectiva
,
convexa
e
discreta
son tres subdisciplinas da xeometria actual que tratan con estas e outras cuestions relacionadas.
Estudando problemas como o das
sete pontes de Konigsberg
,
Leonhard Euler
considerou que as propiedades mais fundamentais das figuras xeometricas se basean so na forma, independentemente das suas propiedades metricas. Euler chamou a esta nova rama da xeometria
xeometria situs
(xeometria de lugar), mais hoxe en dia e conecida como
topoloxia
. A topoloxia medrou ata tal punto que se converteu nunha disciplina independente. Dous obxectos tales que deformacions continuas dun deles permiten obter o outro, son topoloxicamente equivalentes. Os obxectos poden non obstante conservar algunha xeometria, como no caso dos
nos hiperbolicos
.
A
xeometria diferencial
usa ferramentas do
calculo infinitesimal
para estudar problemas en xeometria.
Durante preto de dous mil anos desde Euclides, mentres se ampliaba inevitabelmente o numero de cuestions xeometricas propostas e resoltas, a concepcion basica de
espazo
permaneceu en esencia inalterabel.
Immanuel Kant
arguiu que hai soamente unha xeometria
absoluta
, a cal e reconecida como verdadeira
a priori
por unha facultade interior da mente: a xeometria euclidiana era
sintetica a priori
[
2
]
. Esta opinion dominante cambiou a partir do descubrimento revolucionario da xeometria non euclidiana nos traballos de Carl Friedrich Gauss (quen nunca publicou a sua teoria), Bolyai e Lobachevsky, os cales demostraron que o espazo euclidiano ordinario e so unha das posibilidades de desenvolvemento da xeometria. Unha ampla vision da materia da xeometria foi daquela expresada por
Riemann
na sua leccion inaugural de
1867
Uber die Hypothesen, welche der Geometrie zu Grunde liegen
(
Sobre as hipoteses nas que se basea a xeometria
)
[
3
]
, publicado soamente despois da sua morte. A nova idea de espazo de Riemann foi crucial en dous dos piares da xeometria moderna, a
teoria da relatividade xeral
de
Einstein
e a
xeometria riemanniana
, que consideran espazos mais xerais nos que se define a nocion de lonxitude.
Onde a xeometria tradicional permitia dimensions 1 (xeometria da recta), 2 (xeometria plana) e 3 (o mundo que nos rodea concibido como un espazo tridimensional: xeometria do espazo), os matematicos levan usando dimensions superiores durante case dous seculos. A dimension pasou de ser un
numero natural
calquera
n
, posibelmente
infinito
coa introducion do
espazo de Hilbert
, a poder ser calquera
numero real
positivo na
xeometria fractal
. A
teoria da dimension
e unha area tecnica, inicialmente dentro da topoloxia xeral, que discute
definicions
; a dimension e agora definida mais como unha intuicion, como a maioria das ideas matematicas. As
variedades topoloxicas
conectadas tenen unha dimension ben definida; isto e, mais que nada
a priori
, un teorema (
invarianza do dominio
).
O asunto da dimension ainda importa a xeometria, na ausencia de respostas completas as preguntas clasicas. Dimensions 3 do espazo e 4 do
espazo-tempo
son casos especiais en
topoloxia xeometrica
. Dimension 10 ou 11 e un numero clave na
teoria de cordas
. A investigacion debe traer unha razon
xeometrica
satisfactoria ao significado das dimensions 10 e 11.
Unha
teselacion
no
plano hiperbolico
.
O tema da
simetria
na xeometria e case tan antigo como a propia xeometria. As formas simetricas como o circulo, os
poligonos regulares
e os
solidos platonicos
tiveron un profundo significado para moitos dos filosofos da antiguidade e foron investigados con detalle antes da epoca de Euclides.
Os patrons simetricos aparecen con asiduidade na natureza e foron usados artisticamente en multitude de formas, incluidas as obras de
M. C. Escher
. Poren, non foi ata a segunda metade do seculo XIX que foi reconecido o rol unificador da simetria nos fundamentos da xeometria. O
programa de Erlangen
de
Felix Klein
proclamaba que, nun sentido moi preciso, a simetria, expresada a traves da nocion dun
grupo
de transformacion, determina que
e
xeometria. A simetria na xeometria euclidiana clasica representase por
congruencias
e movementos rixidos, mentres que na xeometria proxectiva un rol analogo xogano as
colineacions
, transformacions xeometricas que aplican rectas en rectas. Poren foi nas novas xeometrias de Bolyai e Lobachevsky, Riemann,
Clifford
e Klein, e
Sophus Lie
, que a idea de Klein de "definir unha xeometria por medio dun
grupo de simetria
" demostrou ter maior influencia. Tanto a simetria discreta como a continua tenen roles prominentes en xeometria, a primeira en topoloxia e na
teoria xeometrica de grupos
, a segunda na
teoria de Lie
e na xeometria riemanniana.
Un tipo diferente de simetria e o principio de
dualidade
na xeometria proxectiva entre outros campos. Este metafenomeno pode ser descrito a grandes trazos como segue: se en calquera teorema se cambia "punto" por "plano", "unir" por "xuntar" e "xacer" por "conter", obtense outro teorema igualmente certo. Unha forma de dualidade similar e moi relacionada e a existente entre un
espazo vectorial
e o seu espazo dual.
Un
europeo
e un
arabe
practicando xeometria no
seculo XV
.
frontispicio
da primeira version inglesa dos
Elementos de Euclides
de Sir Henry Billingsley,
1570
.
Os primeiros rexistros da xeometria remontanse ao segundo milenio antes de Cristo en
Mesopotamia
e no
Antigo Exipto
[
4
]
[
5
]
. A xeometria desta epoca era unha coleccion de principios descubertos empiricamente relativos a lonxitudes, angulos, areas e volumes, que foron desenvolvidos para a sua aplicacion practica en
topografia
,
construcion
,
astronomia
e outros campos. Os textos de xeometria mais antigos que se conecen son o
Papiro de Rhind
(2000?1800 a.C.) e o
Papiro de Moscova
(c. 1890 a.C.) exipcios; e as taboas de arxila
babilonias
, como a
Plimpton 322
(1900 a.C.). Por exemplo, o Papiro de Moscova proporciona unha formula para calcular o volume dunha
piramide
truncada
[
6
]
. Ao sur de Exipto, os
antigos nubios
estableceron un sistema xeometrico que incluia versions temperas de
reloxos de sol
[
7
]
[
8
]
.
No
seculo VII a.C.
, o matematico grego Tales de Mileto usou a xeometria para resolver problemas tales como o calculo da altura de piramides ou a distancia dun barco da costa. Atribueselle o primeiro uso do
razoamento dedutivo
aplicado a xeometria, ao derivar catro
corolarios
do
Teorema de Tales
[
6
]
.
Pitagoras
estableceu a
Escola pitagorica
, da que se acredita ser a primeira en demostrar o
Teorema de Pitagoras
[
9
]
, ainda que o estado do teorema ten unha longa historia
[
10
]
[
11
]
.
Eudoxo
(408?c.355 a.C.) desenvolveu o
metodo exhaustivo
, que permitia o calculo de areas e volumes de figuras curvilineas
[
6
]
, asi como unha teoria de proporcions que evitaban o problema das magnitudes inconmensurabeis, e que fixo posibeis os significativos avances dos xeometras subsecuentes. Arredor do 300 a.C.,
Euclides
revolucionou a xeometria cos seus
Elementos
, amplamente considerado como o libro de texto de mais exito e mais influente de todos os tempos
[
6
]
, e que introducia o rigor matematico mediante o
metodo axiomatico
, un exemplo temperan do formato que mesmo hoxe se usa en matematicas, cos conceptos de
definicion
,
axioma
,
teorema
e
demostracion
. Se ben a maioria dos contidos dos
Elementos
xa eran conecidos, Euclides expuxoos nun marco sinxelo e con coherencia loxica
[
6
]
.
Os Elementos
eran conecidos pola xente educada do mundo occidental ata mediados do
seculo XX
, e os seus contidos ainda se ensinan hoxe nas clases de xeometria
[
12
]
.
Arquimedes
de
Siracusa
(c.287?212 a.C.) usou o metodo exhaustivo para calcular a area comprendida entre unha
parabola
e unha
recta
perpendicular ao seu eixe, mediante a suma dunha
serie
infinita; e deu unha aproximacion notabel do
numero Pi
[
13
]
. Tamen estudou as
espirais
que levan o seu nome e obtivo formulas para o volume de
superficies de revolucion
.
Muller ensinando xeometria. Ilustracion nunha traducion medieval dos
Elementos de Euclides
, (c.1310).
As matematicas do
islam
contribuiron na
Idade Media
ao desenvolvemento da xeometria, especialmente da
xeometria alxebrica
[
14
]
e a
alxebra xeometrica
[
15
]
.
Al-Mahani
(n. 853) concibia a idea de reducir os problemas xeometricos, tales como a
duplicacion do cubo
, a problemas alxebricos
[
16
]
.
Th?bit ibn Qurra
(conecido como Thebit en
latin
) (836?901) traballou con operacions aritmeticas aplicadas as razons de cantidades xeometricas, e contribuiu ao desenvolvemento da
xeometria analitica
[
17
]
.
Omar Khayyam
(1048?1131) achou solucions xeometricas para as
ecuacions cubicas
[
18
]
. Os teoremas de Ibn al-Haytham (
Alhazen
), Omar Khayyam e
Nasir al-Din al-Tusi
sobre
cuadrilateros
, incluidos os cuadrilateros de
Lambert
e de
Saccheri
, foron resultados temperans da
xeometria hiperbolica
; e xunto cos seus postulados alternativos, como o
Axioma de Playfair
, tiveron unha considerable influencia no desenvolvemento da xeometria non euclidiana entre os xeometras europeos posteriores:
Witelo
(c.1230?c.1314),
Gersonides
(1288?1344),
Alfonso de Valladolid
,
John Wallis
, e
Giovanni Girolamo Saccheri
[
19
]
.
A comezos do
seculo XVII
houbo dous desenvolvementos importantes na xeometria. O primeiro e a creacion da xeometria analitica, ou xeometria con coordenadas e ecuacions, por
Rene Descartes
(1596?1650) e
Pierre de Fermat
(1601?1665). Isto foi un precursor necesario da
analise matematica
e da
fisica
como ciencia cuantitativa precisa. O segundo feito foi o estudo sistematico da
xeometria proxectiva
por
Girard Desargues
(1591?1661). A xeometria proxectiva e unha xeometria sen medida ou linas paralelas, so estuda como estan relacionados entre si os puntos.
No
seculo XIX
dous feitos cambiaron o modo de estudo que vina sendo usado ata enton. Foron o descubrimento das xeometrias non euclidianas por
Nikolai Ivanovich Lobachevsky
(1792?1856),
Janos Bolyai
(1802?1860) e
Carl Friedrich Gauss
(1777?1855); e a formulacion da
simetria
como unha consideracion central no
Programa de Erlangen
de
Felix Klein
(que xeneralizou as xeometrias euclidianas e non euclidianas). Dous dos mais grandes xeometras da epoca foron
Bernhard Riemann
(1826?1866), quen traballou inicialmente con ferramentas da analise matematica e introduciu a
superficie de Riemann
, e
Henri Poincare
, o fundador da
topoloxia alxebrica
e a teoria xeometrica dos
sistemas dinamicos
. Como consecuencia destes cambios na concepcion da xeometria, o concepto de
espazo
tornouse mais rico e variado, e fixo dela o escenario natural de teorias tan diferentes como a
analise complexa
e a
mecanica clasica
.
O politopo 4
21
proxectado ortogonalmente no
grupo de Lie
E
8
do
plano de Coxeter
.
A xeometria euclidiana foise relacionando intimamente coa
xeometria computacional
, a
computacion grafica
, a
xeometria convexa
, a
xeometria discreta
, e algunhas areas da
combinatoria
. O impulso a traballos posteriores de xeometria euclidiana e grupos euclidianos foi dado pola
cristalografia
e o traballo de
H. S. M. Coxeter
e o resultado pode verse nas teorias dos
grupos de Coxeter
e os
politopos
. A teoria de
grupos xeometricos
e unha extension da mais xeral teoria de
grupos discretos
, avanzando modelos xeometricos e tecnicas alxebricas.
A
xeometria diferencial
ten incrementado a sua importancia na
fisica matematica
debido a
teoria xeral da relatividade
de
Einstein
, a cal postula que o
universo
e
curvo
. A xeometria diferencial contemporanea e
intrinseca
, o cal significa que os espazos que considera son
variedades diferenciabeis
cuxa estrutura xeometrica e gobernada por unha
metrica de Riemann
, a cal determina como se miden distancias nas proximidades de cada punto
Un espesamento dun
no de trevo
.
O campo da
topoloxia
, que tivo un gran crecemento no
seculo XX
, e, nun sentido tecnico, un tipo de
transformacion xeometrica
na que as transformacions son
homeomorfismos
. Isto ten sido expresado frecuentemente coa frase "a topoloxia e unha xeometria de goma de borrar". A maioria dos matematicos considerarian como partes da xeometria as contemporaneas
xeometria topoloxica
e
topoloxia diferencial
, e subcampos particulares como a
teoria de Morse
. A
topoloxia alxebrica
e a
topoloxia xeral
seguiron os seus propios caminos.
Variedade de Calabi?Yau
de dimension 5.
O campo da
xeometria alxebrica
e a version moderna da
xeometria cartesiana
de coordenadas. Desde finais dos anos 50 ata mediados dos 70 do seculo XX sufriu un desenvolvemento esencial dos seus fundamentos, debido principalmente aos traballos de
Jean-Pierre Serre
e
Alexander Grothendieck
. Isto levou a introducion de
esquemas
e a unha maior enfase nos metodos
topoloxicos
, incluindo varias teorias
cohomoloxicas
. Un dos sete
Problemas do Milenio
, a
conxectura de Hodge
, e unha cuestion de xeometria alxebrica.
O estudo de variedades alxebricas de baixa dimension,
curvas alxebricas
,
superficies alxebricas
e variedades alxebricas de dimension 3, avanzou moito. A teoria das
bases de Grobner
e a
xeometria alxebrica real
estan entre os subcampos de mais aplicacion da moderna xeometria alxebrica. A
xeometria aritmetica
e unha activa rama que combina a xeometria alxebrica e a
teoria de numeros
. Outras linas de investigacion atinxen aos
espazos de modulos
e a
xeometria complexa
. Os metodos alxebrico-xeometricos aplicanse comunmente nas teorias de
cordas
e de
branas
.
- ↑
Turner, Martin J.; Blackledge, Jonathan M.; Andrews, Patrick R. (1998). Academic Press, ed.
Fractal geometry in digital imaging
(en ingles)
. p. 1.
ISBN
0-12-703970-8
. Consultado o 8 de agosto de 2013
.
- ↑
Kline, Morris
(1990) [1972]. Oxford University Press, ed.
Mathematical thought from ancient to modern times
(en ingles)
III
. p. 1032.
ISBN
0-19-506137-3
. Consultado o 14 de agosto de 2013
.
Kant non rexeitaba a
posibilidade
loxica (analitica a priori) da xeometria non euclidiana, vexase
Gray, Jeremy
(1989) [1979]. Oxford University Press, ed.
Ideas of Space Euclidean, Non-Euclidean, and Relativistic
(en ingles)
(2 ed.). p. 85.
ISBN
978-0198539353
. Consultado o 14 de agosto de 2013
.
Alguns autores suxeriron que, tendo en conta o anterior, Kant predixo de feito o desenvolvemento da xeometria non euclidiana, cf.
Nelson, Leonard (1965). "Philosophy and Axiomatics". En Dover Publications.
Socratic Method and Critical Philosophy
(en ingles)
. p. 164
. Consultado o 14 de agosto de 2013
.
- ↑
D.R. Wilkins.
"Ligazons a leccion inaugural de Riemann"
. Dublin: Trinity College
. Consultado o 14 de agosto de 2013
.
- ↑
Friberg, J. (1981). "Methods and traditions of Babylonian mathematics. Plimpton 322, Pythagorean triples, and the Babylonian triangle parameter equations".
Historia Mathematica
(en ingles)
8
: 277?318.
- ↑
Neugebauer, Otto
(1969) [1957]. "IV:Egyptian Mathematics and Astronomy". En Dover Publications.
The Exact Sciences in Antiquity
(en ingles)
(2 ed.). pp. 71?96.
ISBN
978-0-486-22332-2
.
- ↑
6,0
6,1
6,2
6,3
6,4
Boyer, Carl B.
(1986) [1968]. Alianza Editorial, ed.
A History of Mathematics
[
Historia de la Matematica
]
(en castelan)
. Madrid. pp. 41, 76, 129, 141, 145.
ISBN
84-206-8094-X
.
- ↑
"Gnomons at Meroe and Early Trigonometry"
.
The Journal of Egyptian Archaeology
(en ingles)
84
: 171. 1998
. Consultado o 9 de agosto de 2013
.
- ↑
Andrew L. Slayman (27 de maio de 1998). Archaeology.org, ed.
"Neolithic Skywatchers"
(en ingles)
. Consultado o 9 de agosto de 2013
.
- ↑
Eves, Howard (1990). Saunders Series, ed.
An Introduction to the History of Mathematics
(en ingles)
.
ISBN
0-03-029558-0
. Consultado o 8 de agosto de 2013
.
- ↑
Kurt Von Fritz (1945). "The Discovery of Incommensurability by Hippasus of Metapontum".
The Annals of Mathematics
(en ingles)
.
- ↑
James R. Choike (1980). "The Pentagram and the Discovery of an Irrational Number".
The Two-Year College Mathematics Journal
(en ingles)
.
- ↑
Eves, Howard
(1990). Saunders College Publishing, ed.
An Introduction to the History of Mathematics
(en ingles)
(6 ed.). p. 141.
ISBN
0-03-029558-0
. Consultado o 14 de agosto de 2013
.
Ningun outro libro, agas a Biblia, foi tan amplamente usado...
- ↑
O'Connor, J.J. e Robertson, E.F. (Febreiro 1996). University of St Andrews, ed.
"A history of calculus"
(en ingles)
. Arquivado dende
o orixinal
o 15 de xullo de 2007
. Consultado o
2007-08-09
.
- ↑
Rashed, Roshdi (1994). Springer, ed.
The development of Arabic mathematics: between arithmetic and algebra
(en ingles)
. Londres. p. 35.
ISBN
0-7923-2565-6
. Consultado o 9 de agosto de 2013
.
- ↑
Boyer, Carl B.
(1986) [1968]. "La hegemonia arabe". En Alianza Editorial.
A History of Mathematics
[
Historia de la Matematica
]
(en castelan)
. Madrid. pp. 311?312.
ISBN
84-206-8094-X
.
...Tratase de Omar Khayyam (ca. 1050?1123), o "fabricante de tendas", que escribiu unha
Alxebra
que estendia a clasica de Al-Khwarizmi ata incluir as ecuacions cubicas. Seguindo a tradicion dos seus predecesores arabes, Omar Khayyam da os dous tipos de solucions, aritmeticas e xeometricas, para as ecuacions cuadraticas; acerca das ecuacions cubicas en xeral semella ter crido (erroneamente, como se chegaria a demostrar mais tarde, durante o seculo XVI) que era imposibel dar solucions aritmeticas, e xa que logo Omar Khayyam da unicamente solucions xeometricas nestes casos. A idea de utilizar interseccions de conicas para resolver ecuacions cubicas non era nova, xa fora explorada por Menecmo, Arquimedes e Alhazen, mais Omar Khayyam deu o paso decisivo de xeneralizar o metodo para cubrir todas as ecuacions cubicas que tenan algunha raiz positiva... Para as ecuacions de grao maior ca tres Omar Khayyam evidentemente non tentou utilizar metodos xeometricos analogos, pola sinxela razon de que o espazo non ten mais ca tres dimensions... Unha das contribucions mais frutiferas do eclecticismo arabe neste caso, foi a tendencia a pechar o antigo abismo aberto entre a alxebra numerica e a alxebra xeometrica. O paso decisivo nesta direccion deuno Descartes moito mais tarde, mais Omar Khayyam xa se movia polo mesmo camino ao afirmar que: "Quenquera que pense que a alxebra e un sistema de trucos para obter os valores das incognitas pensa vanamente. Non se debe prestar ningunha atencion ao feito de que a alxebra e a xeometria son en aparencia diferentes. Os feitos da alxebra son feitos xeometricos que estan demostrados".
- ↑
School of Mathematics and Statistics, University of St Andrews, Scotland (ed.).
"Al-Mahani"
.
MacTutor Biography
(en ingles)
. Consultado o 9 de agosto de 2013
.
- ↑
School of Mathematics and Statistics, University of St Andrews, Scotland (ed.).
"Al-Sabi Thabit ibn Qurra al-Harrani"
.
MacTutor Biography
(en ingles)
. Consultado o 9 de agosto de 2013
.
- ↑
School of Mathematics and Statistics, University of St Andrews, Scotland (ed.).
"Omar Khayyam"
.
MacTutor Biography
(en ingles)
. Consultado o 9 de agosto de 2013
.
- ↑
Rosenfeld, Boris A.; Youschkevitch, Adolf P. (1996). "Geometry". En Rashed, Roshdi.
Encyclopedia of the History of Arabic Science
(en ingles)
2
. Londres e Nova York: Routledge. pp. 447?494 [470]
. Consultado o 14 de agosto de 2013
.
Tres cientificos, Ibn Al-Haytham, Khayyam, e Al-Tusi, fixeron as contribucions mais considerabeis a esta rama da xeometria cuxa importancia foi plenamente reconecida no seculo XIX. En esencia, as suas proposicions concernentes as propiedades dos cuadrilateros que consideran, asumindo que algun dos angulos desas figuras fora agudo ou obtuso, englobaban uns poucos teoremas iniciais das xeometrias hiperbolica e eliptica. As suas outras propostas mostraban que varias afirmacions xeometricas eran equivalentes ao quinto postulado de Euclides. E extremadamente importante que estes estudosos estableceran a conexion mutua entre este postulado e a suma dos angulos dun triangulo e un cuadrilatero. A traves dos seus traballos sobre a teoria de rectas paralelas, os matematicos arabes influenciaron directamente as relevantes investigacions dos seus colegas europeos. O primeiro intento europeo de probar o postulado das rectas paralelas – feito por Witelo, o cientifico polaco do seculo XIII, mentres revisaba o
Libro de Optica
de Ibn al-Haytham (
Kitab al-Manazir
) – estaba sen dubida inspirado por fontes arabes. As demostracions propostas no seculo XIV polo sabio xudeu Levi ben Gerson quen viviu no sur de Francia, e polo anteriormente mencionado Afonso desde Espana, aproximabanse moito a demostracion de Ibn al-Haytham. Antes, tinamos demostrado que a
Exposicion Pseudo-Tusi de Euclides
estimulou os estudos da teoria de linas paralelas de J. Wallis e G. Saccheri
- Boyer, Carl B.
(1986) [1968]. Alianza Editorial, ed.
A History of Mathematics
[
Historia de la Matematica
]
(en castelan)
. Madrid.
ISBN
84-206-8094-X
.
- Lobachevsky, Nikolai I.
(2010). European Mathematical Society, A. Papadopoulos, ed.
Pangeometry
. Heritage of European Mathematics
(en ingles)
4
.
- Mlodinow, M. (1992). Allen Lane, ed.
Euclid's window (the story of geometry from parallel lines to hyperspace)
(en ingles)
.