 Representation d'un triangle ABC rectangle en C.
Representation d'un triangle ABC rectangle en C.
En
geometrie euclidienne
, un
triangle rectangle
est un
triangle
dont l'un des
angles
est
droit
. Les deux autres angles sont alors
complementaires
, de mesure strictement inferieure
[
1
]
. On nomme alors
hypotenuse
le cote oppose a l'angle droit. Les deux autres cotes, adjacents a l’angle droit, sont appeles
cathetes
.
L’hypotenuse est alors le plus grand cote du triangle, et sa longueur est reliee a celles des deux autres cotes par le
theoreme de Pythagore
. Cette relation est meme caracteristique des triangles rectangles. Dans le cas des triangles a cotes entiers, elle mene a la definition des
triplets pythagoriciens
.
Le theoreme de Pythagore precise que dans un triangle rectangle, le carre de la longueur de l'hypotenuse est egal a la somme des carres des deux autres longueurs des cotes de l’angle droit, autrement dit, si un triangle
ABC
est rectangle en
C
, alors
 .
.
Reciproquement, tout triangle
ABC
verifiant l'egalite precedente est un triangle rectangle en
C
.
Comme un triangle rectangle peut se realiser comme la moitie d’un rectangle engendre par les deux cathetes, l’aire d’un triangle rectangle est egale a la moitie du produit des longueurs de ces deux cotes.
Recriproquement, si l’aire d’un triangle est le produit des longueurs de deux cotes divise par 2, alors ce triangle est rectangle au sommet commun a ces cotes.
 Mediane de l'angle droit d'un triangle rectangle
Mediane de l'angle droit d'un triangle rectangle
Si un triangle est rectangle, alors le milieu de l’hypotenuse est a egale distance des trois sommets, c’est-a-dire qu’il est le centre du
cercle circonscrit
, ou encore que la mediane issue de l’angle droit a pour longueur la moitie de l’hypotenuse
[
2
]
.
Reciproquement, tout point d’un cercle forme un triangle rectangle avec les extremites d’un diametre de ce cercle.
Cette equivalence peut etre vue comme un cas particulier du
theoreme de l'angle au centre
: l’angle inscrit est droit si et seulement si l’angle au centre est plat.
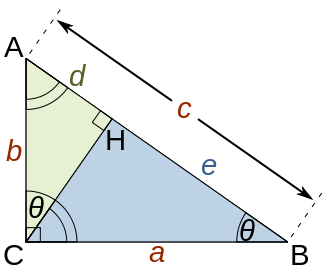 Triangle rectangle et pied de la hauteur
Triangle rectangle et pied de la hauteur
La
hauteur
issue de l'angle droit d'un triangle rectangle possede des proprietes caracteristiques dont l'une apparait dans les premieres pages du livre de
Rene Descartes
,
La geometrie
.
Dans tout triangle ABC dont H est le pied de la hauteur issue de C.
- Si le triangle est rectangle en C alors
[
3
]
:
- H appartient a [AB] et CH
2
= HA × HB ;
- H appartient a [AB] et AC
2
= AH × AB ;
- H appartient a [AB] et BC
2
= BH × AB ;
- CH × AB = CA × CB.
- Reciproquement, un triangle dans lequel l'une de ces quatre proprietes est realisee est rectangle en C.
Les trois premieres proprietes se deduisent de l'observation des trois
triangles semblables
ABC, CBH et ACH. La quatrieme consiste a ecrire l'aire du triangle rectangle en considerant successivement BC et BA comme base.
Les reciproques utilisent les memes outils : les premieres egalites traduisent des egalites de rapports et la presence d'un angle droit ou d'un angle en commun confirment la presence de triangles semblables, qui sont donc rectangles.
L'orthocentre d'un triangle rectangle est de maniere evidente le sommet ou se trouve l'angle droit.
Dans un triangle rectangle, la hauteur issue de l'angle droit, a une longueur HC egale a la somme des rayons des cercles inscrits respectivement dans le triangle rectangle initial ABC et les deux triangles rectangles delimites par la hauteur. Si on appelle
r
le rayon du cercle inscrit dans le triangle ABC,
r
1
celui du cercle inscrit dans le triangle AHC,
r
2
celui du cercle inscrit dans le triangle BHC, et
h
la hauteur
CH
, on a :

La hauteur
h
, les rayons
r
,
r
1
et
r
2
sont lies par les relations :
 et
et


et
 .
.
 Triangle rectangle et son cercle inscrit
Triangle rectangle et son cercle inscrit
Dans tout triangle rectangle, les
bissectrices
se rencontrent en un point O centre du
cercle inscrit
dans le triangle. Le rayon de ce cercle est egal au demi-perimetre
p
moins l'hypotenuse (voir schema) soit, avec les notations precedentes :
 .
.
On retrouve le
theoreme de Carnot
, qui, applique au triangle rectangle en C, donne,
r
etant le rayon du cercle inscrit, et
R
=
AB
/
2
celui du cercle circonscrit :
CA + CB
/
2
=
r
+
R
et
CA + CB = AB + 2
r
Comme dans tout triangle, le rayon
r
du cercle inscrit est aussi egal a deux fois l'aire du triangle divisee par le perimetre, soit
 .
.
Les rayons des
cercles exinscrits
sont
 .
.
Ces triangles sont uniques a similitude pres.
Le
demi-carre
est un
triangle isocele rectangle
. Ses deux angles aigus mesurent 45°, et le rapport entre son hypotenuse et chacune de ses
cathetes
vaut
√
2
.

Le triangle 3-4-5 est un triangle dont les cotes mesurent respectivement 3, 4 et 5 unites. Il s’agit du triangle rectangle a cotes entiers avec l’hypotenuse minimale, et le seul triangle dont les longueurs de cotes suivent une progression arithmetique (a un facteur multiplicatif pres)
[
4
]
. Cette forme est mise a profit pour obtenir un angle droit a l’aide de la
corde a 13 nœuds
.

Le
triangle de Kepler
est le seul triangle rectangle dont les longueurs de cotes suivent une progression geometrique. La raison de cette progression est la racine carree du
nombre d'or
.

 Triangle rectangle d'angles 30° - 60° - 90° avec une
hypotenuse
de longueur 1.
Triangle rectangle d'angles 30° - 60° - 90° avec une
hypotenuse
de longueur 1.
Le demi-triangle equilateral a pour angles 90°, 60° et 30°.
C’est le seul triangle rectangle dont les angles suivent une progression arithmetique
[
ref.
souhaitee]
.
Tout triangle non plat peut etre decompose en deux triangles rectangles admettant pour cote commun une hauteur interne (par exemple, celle issue d’un sommet d’angle maximal).
Ce principe permet de ramener les problemes de pavages par des polygones a des problemes de pavage par des triangles rectangles.
Dans un
repere orthonorme
 , si un point
M
se projette selon
H
sur l'axe
, si un point
M
se projette selon
H
sur l'axe
 et selon
I
sur l'axe
et selon
I
sur l'axe
 , alors
OHM
et
OMI
sont des triangles rectangles.
, alors
OHM
et
OMI
sont des triangles rectangles.


Un triangle rectangle comporte un angle droit et deux
angles aigus
, du moins en geometrie euclidienne (
sur une sphere
, il existe des triangles a deux et meme trois angles droits).
Deux triangles rectangles ayant un de leurs
angles
non droits egaux sont
semblables
: le rapport de deux des cotes du triangle rectangle ne depend donc que d'un angle non droit. Cette propriete permet d'introduire les
fonctions trigonometriques
pour un angle aigu non oriente, dont la mesure est, en degre entre 0 et 90° (ou en radians, entre 0 et π/2). Par exemple pour un triangle ABC rectangle en C :
- le
cosinus
de l'angle α est le rapport du cote de l'angle droit adjacent a α par l'
hypotenuse
, soit cos(α) =
AC
/
AB
;
- le
sinus
de l'angle α est le rapport du cote de l'angle droit oppose a α par l'hypotenuse, soit sin(α) =
BC
/
AB
;
- la
tangente
de l'angle α est le rapport du cote de l'angle droit oppose a α par cote de l'angle droit adjacent a α, tan(α) =
BC
/
AC
.
 Le triangle 3-4-5, un exemple bien connu de triangle rectangle pythagoricien
Le triangle 3-4-5, un exemple bien connu de triangle rectangle pythagoricien
Un triangle rectangle dont les trois cotes sont mesures par des nombres entiers (pour une meme unite de mesure) est appele triangle pythagoricien. Par le
theoreme de Pythagore
, les longueurs des trois cotes d'un triangle pythagoricien fournissent un
triplet pythagoricien
, qui est un triplet de
nombres entiers
(
x
,
y
,
z
)
non nuls verifiant
x
2
+
y
2
=
z
2
. Par la reciproque du meme theoreme, un triplet pythagoricien permet de construire un triangle pythagoricien.
En particulier pour tout nombre entier
n
superieur ou egal a 3, on peut construire un triangle rectangle dont la longueur d'un cote de l'angle droit est mesuree par ce nombre
n
, les deux autres cotes etant mesures par des nombres entiers :
- Si
n
est un nombre pair,
n
= 2
k
, il suffit de prendre la longueur de l'autre cote de l'angle droit egale a
k
2
? 1
. L'hypotenuse est alors de longueur egale a
k
2
+ 1
.
- Si
n
est un nombre impair,
n
= 2
k
+ 1
, il suffit de prendre la longueur de l'autre cote de l'angle droit egale a
2
k
2
+ 2
k
. L'hypotenuse est alors de longueur egale a
2
k
2
+ 2
k
+ 1
.
On sait decrire plus generalement tous les triplets, et donc tous les triangles, pythagoriciens.
Fermat
a demontre
qu'aucun de ceux-ci ne pouvait avoir pour aire un
carre parfait
.
La spirale de Theodore est constituee d’une suite de triangles rectangles, chacun admettant une cathete de longueur 1 et l’autre definie par l’hypotenuse du triangle precedent. Le triangle initial est isocele rectangle. La suite des longueurs des hypotenuses est constituee des racines carrees des entiers naturels. Cette spirale est nommee en hommage a
Theodore de Cyrene
qui aurait demontre que les racines carrees des premiers entiers (hors carres parfaits) etaient
irrationnelles
.
Un
tetraedre
est dit trirectangle si trois de ses faces sont des triangles rectangles en un meme sommet. Le
theoreme de de Gua
generalise alors le theoreme de Pythagore en stipulant que le carre de l’aire de la derniere face est la somme des carres des aires des trois autres.
 Representation d'un triangle trirectangle.
Representation d'un triangle trirectangle.
En
geometrie non euclidienne
, un triangle rectangle spherique peut posseder deux ou trois angles droits
[
5
]
.
- ↑
Si on exclut la possibilite que deux sommets soient confondus, un triangle ne peut admettre deux angles droits et un angle nul.
- ↑
propriete caracteristique parfois attribuee a
Thales
.
- ↑
≪
Les relations metriques dans le triangle rectangle
≫, sur
alloprof.qc.ca
.
- ↑
Raymond A. Beauregard et E. R. Suryanarayan, ≪
Arithmetic triangles
≫,
Mathematics Magazine
,
vol.
70,
n
o
2,
,
p.
105?115
(
DOI
10.2307/2691431
,
MR
1448883
)
.
- ↑
Joseph Casimir Pascal,
Cours de geometrie elementaire
, Bachelier,
, 367
p.
(
lire en ligne
)
.
Sur les autres projets Wikimedia :
|
|---|
| Description
|
|
| Types
|
|
| Points remarquables (
Nombre de Kimberling
)
|
|
| Droites remarquables
|
|
| Cercles remarquables
|
|
| Triangles remarquables
|
|
| Courbes remarquables
|
|
| Theoremes
|
|
| Relations entre triangles
|
|
| Resolution
|
|