En
physique
, l'
analyse spectrale
recouvre plusieurs techniques de description de signaux (variables selon le temps ou, plus rarement, dans l'espace) dans le domaine des frequences. Elle permet en particulier d'obtenir les caracteristiques de la reponse d'un
systeme lineaire
en utilisant une
fonction de transfert
. En mathematiques, l'
analyse harmonique
correspond a une partie de ces techniques.
Un
phenomene physique
dependant du temps est decrit par un ou plusieurs signaux. On ne peut qu'exceptionnellement les interpreter de facon simple. Le probleme est de trouver une description de leur contenu, relativement generale et adaptee aux problemes concrets. Ceux-ci se presentent souvent de la maniere suivante : un systeme transforme un signal d'entree en un signal de sortie, comment determiner les caracteristiques de celui-ci en fonction de celles du signal d'entree et de celles du systeme ?
Dans le cas general, on ne connait malheureusement pas la relation entre les valeurs du signal de sortie et celles du signal d'entree mais seulement la relation entre les variations du signal de sortie et les valeurs (ou eventuellement les variations) du signal d'entree. En termes
mathematiques
, le systeme est regi par une
equation differentielle
. Si celle-ci est quelconque, le probleme est insoluble.
Heureusement, il existe une classe importante de systemes, les systemes lineaires (ou supposes tels) regis par le principe de superposition. Dans ce cas, correspondant a une equation differentielle lineaire, on peut essayer de decomposer le signal d'entree en une somme de signaux simples auxquels on saurait faire correspondre des signaux de sortie egalement simples dont la somme donnerait le resultat cherche.
Le probleme se simplifie encore plus si les caracteristiques du systeme restent constantes au cours du temps. On a affaire a une equation differentielle lineaire a coefficients constants. Les signaux simples sont les
sinusoides
qui subissent uniquement une amplification et un dephasage. C'est le probleme de l'analyse spectrale : decomposer un signal complique en une somme de sinusoides.
Ici apparait une difficulte car cette decomposition exige que le signal soit defini sur un temps infini. Or il ne peut etre connu qu'a travers un enregistrement de duree limitee : il faut donc construire un modele du signal en faisant des hypotheses, souvent evidentes intuitivement, sur la partie non enregistree du phenomene.
On peut supposer, par exemple, que le signal reproduit indefiniment le contenu de l'enregistrement : on construit alors un modele periodique base sur la
serie de Fourier
. Le signal est decrit par un spectre discret (ensemble de frequences en progression arithmetique).
On peut aussi supposer que le niveau du signal est negligeable en dehors de l'enregistrement : on utilise dans ce cas un modele transitoire base sur la
transformation de Fourier
qui conduit en general a un spectre continu.
Il existe un certain nombre de phenomenes naturels pour lesquels aucune de ces deux hypotheses n'est realiste. Par exemple, un enregistrement de vagues, sans montrer de periodicite, ne montre pas non plus de decroissance nette au cours de sa duree relativement faible : on parle alors de signal a variance finie (certains preferent parler de puissance finie mais ce n'est pas toujours pertinent techniquement), ce qui conduit a la notion de
densite spectrale
. On peut alors utiliser une hypothese un peu plus floue selon laquelle la moyenne quadratique calculee sur l'enregistrement fournit une estimation raisonnable de la
moyenne quadratique
du signal. Ce type d'analyse conduit encore a un spectre continu. Il se definit, comme les precedents, a partir du signal mais on peut obtenir des informations supplementaires en considerant celui-ci comme une realisation d'un
processus aleatoire
.
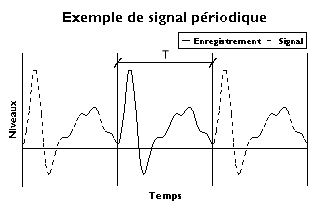
|
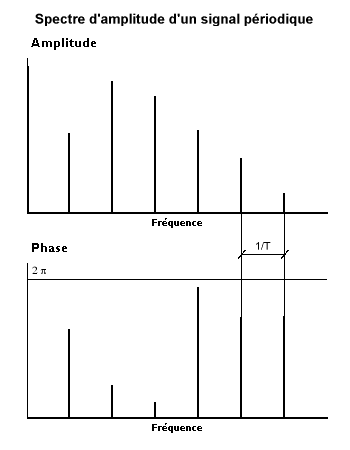
|
Le developpement en serie de Fourier d'un enregistrement de duree
 associe a celui-ci des sinusoides d'amplitudes finies et de frequences multiples de la frequence du fondamental
associe a celui-ci des sinusoides d'amplitudes finies et de frequences multiples de la frequence du fondamental
 . On parle d'un spectre d'amplitude qui est un spectre de raies. Dans le cas general, le resultat de l'analyse peut s'exprimer soit en amplitudes et phases, soit en composantes cosinus et sinus.
. On parle d'un spectre d'amplitude qui est un spectre de raies. Dans le cas general, le resultat de l'analyse peut s'exprimer soit en amplitudes et phases, soit en composantes cosinus et sinus.
La sommation des sinusoides cree un
signal periodique
. Si le signal d'origine est periodique, il est parfaitement represente ? au moins en principe. Dans le cas contraire on n'a represente que l'enregistrement et il faut tenter de trouver autre chose.
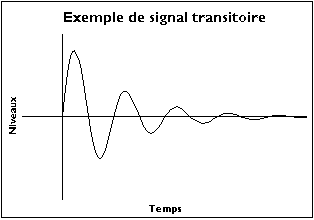 Exemple de signal transitoire
Exemple de signal transitoire
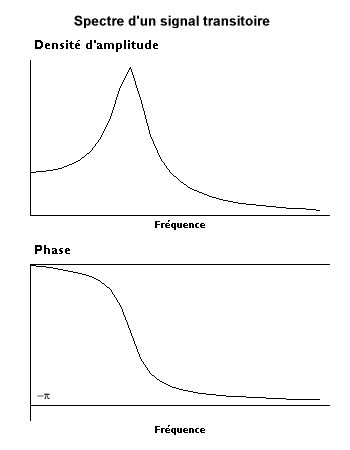
Ici, on raisonnera d'abord sur le signal de duree supposee infinie avant de voir les consequences pour un enregistrement de duree finie. Si ce signal n'est pas periodique, n'a pas de periode finie, on peut essayer de voir ce qui se passerait si on lui pretait une periode infinie. Cela entraine les consequences suivantes :
- Lorsque la duree d'analyse
 tend vers l'infini, le pas de frequence
tend vers l'infini, le pas de frequence
 tend vers 0 : a la limite on passe d'un spectre discret a un spectre continu.
tend vers 0 : a la limite on passe d'un spectre discret a un spectre continu.
- Au cours de cette croissance de la duree d'analyse, lorsque celle-ci est multipliee par un nombre
n
quelconque, le nombre de composantes est multiplie par le meme facteur. Pour que le niveau du signal ne soit pas augmente dans les memes proportions il faut que les amplitudes des composantes soient, en gros, divisees par
n
, ce qui risque de conduire a la limite a des amplitudes nulles. On pare cette difficulte en multipliant les coefficients de Fourier par la longueur d'analyse ou en les divisant par le pas de frequence qui tend vers zero. Ainsi, le spectre continu n'est plus un spectre d'amplitude mais un spectre de densite d'amplitude dont l'unite est unite physique / hertz.
- Malgre ces precautions, la methode peut diverger. Une condition de convergence est que le signal doit etre transitoire : il doit tendre vers 0 lorsque le temps tend vers
 .
.
On obtient ainsi la transformee du signal
 que l'on note generalement
que l'on note generalement
 ,
f
etant la frequence.
,
f
etant la frequence.
Si on retourne a un enregistrement de duree limitee, il y a deux possibilites :
- Le signal n'est different de zero que pendant une duree limitee : l'analyse pendant cette duree fournit, au moins en principe, un resultat exact permettant de reconstituer le signal par inversion de la transformation ;
- Le signal a des valeurs differentes de zero pendant une duree superieure a celle de l'enregistrement : l'imprecision du resultat croit avec la quantite d'information perdue. L'erreur ainsi commise se traduit concretement par une dispersion de l'energie correspondant a une frequence sur les frequences voisines et mathematiquement par la notion de convolution.

Le probleme est plus complique que dans le cas precedent et on peut l'aborder de diverses manieres. Celle que nous utiliserons n'est certainement pas la plus efficace d'un point de vue scientifique mais elle a l'avantage de montrer quelques points essentiels sans les cacher derriere des considerations mathematiques, sinon particulierement difficiles, du moins assez lourdes. Pour s'affranchir de problemes specifiques lies a la prise en compte d'une moyenne non nulle, on supposera que le signal a ete prealablement centre par soustraction de sa moyenne.
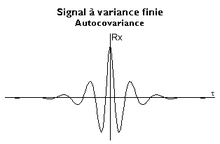
Etant donne un signal
 , on appelle fonction d'
autocovariance
? souvent assimilee a tort a l'
autocorrelation
? la fonction de
, on appelle fonction d'
autocovariance
? souvent assimilee a tort a l'
autocorrelation
? la fonction de
 qui donne la moyenne des produits des valeurs de
qui donne la moyenne des produits des valeurs de
 a deux instants qui different de
a deux instants qui different de
 :
:

Dans le calcul de cette moyenne, t varie de
 a
a
 . Si le signal est transitoire, la fonction est nulle ; s'il est periodique, elle est elle-meme periodique. En se placant dans le cas d'un signal qui n'appartient de toute evidence a aucune des deux categories, la fonction possede les proprietes suivantes :
. Si le signal est transitoire, la fonction est nulle ; s'il est periodique, elle est elle-meme periodique. En se placant dans le cas d'un signal qui n'appartient de toute evidence a aucune des deux categories, la fonction possede les proprietes suivantes :
- le changement de
 en
en
 n'apporte aucune modification : la fonction est paire ;
n'apporte aucune modification : la fonction est paire ;
- a l'origine,
 represente la variance qui est necessairement positive ;
represente la variance qui est necessairement positive ;
- la symetrie impose qu'il s'agisse d'un
extremum
. En fait, il s'agit d'un maximum : si dans le calcul on remplace le decalage 0 par un petit decalage
 , a chaque franchissement du niveau 0, on remplace un petit produit positif par un petit produit negatif ;
, a chaque franchissement du niveau 0, on remplace un petit produit positif par un petit produit negatif ;
- en exceptant le cas du signal periodique, deux points separes par un grand decalage
 ont peu de choses en commun : la fonction tend vers 0 lorsque ce decalage tend vers l'infini ;
ont peu de choses en commun : la fonction tend vers 0 lorsque ce decalage tend vers l'infini ;
- au total, la fonction a souvent une vague allure de sinusoide amortie ;
- on peut, si c'est possible, assimiler le signal a une somme de sinusoides. Supposons que ce soit le cas. Que les amplitudes soient finies ou infiniment petites, on peut ecrire cette somme sous la forme :

Dans ces conditions on montre que

Ainsi :
- la fonction d'autocovariance contient les memes frequences que le signal ;
- les amplitudes ne sont pas identiques mais elles sont obtenues par elevation au carre et division par 2 ;
- les phases ont entierement disparu : l'autocovariance correspond non seulement au signal d'origine, mais aussi a tous ceux qui contiennent les memes composantes.

On peut deduire de ce qui precede :
- la fonction d'autocovariance possede une transformee de Fourier que l'on nomme densite spectrale et que l'on note generalement
 , f etant la frequence ;
, f etant la frequence ;
- les composantes de l'autocovariance etant homogenes a des carres d'amplitude, la densite spectrale est non negative. Elle a une dimension (unite physique)
2
/ Hertz ;
- l'autocovariance etant une fonction reelle et paire, sa transformee de Fourier possede les memes caracteristiques ;
- un enregistrement tronquant toujours le signal cense se maintenir pendant un temps infini, la densite spectrale est necessairement deformee par convolution.
A la deformation du contenu en frequences deja constatee pour les signaux transitoires s'ajoute une incertitude statistique liee a la position de l'enregistrement sur le signal.
La fonction d'autocovariance correspond a toute une famille de signaux qui contiennent les memes composantes. On peut interpreter cette famille comme celle des realisations d'un
processus continu
. Un enregistrement de duree limitee peut egalement etre considere comme une realisation d'un autre processus. Cela permet de preciser avec des intervalles de confiance la valeur statistique de l'analyse effectuee.
- (en)
Y. K.
Lin
,
Probabilistic Theory of Structural Dynamics
, New York, Robert E. Krieger Publishing Company,
, 368
p.
(
ISBN
0-88275-377-0
)