Krystalograficka soustava

Krystalograficka soustava (te? krystalova soustava ) klasifikuje krystalicke pevne latky podle jejich symetrie . Podle typ? symetrie v krystalove m?i?ce se rozli?uje sedm zakladnich krystalografickych soustav. Pro popis krystalicke struktury latek hlavn? v mineralogii, chemii pevnych latek a fyzice pevnych latek se vyu?ivaji prav? krystalograficke soustavy.

Bylo definovano sedm krystalografickych soustav, ktere se li?i osnim ( axialnim) k?i?em protinajicim t?lo krystalu uprost?ed. Jsou to triklinicka , monoklinicka , ortorombicka , tetragonalni , trigonalni , hexagonalni a kubicka soustava. V?echny krystalove struktury, ktere mohou byt definovany stejnym systemem sou?adnych os, pat?i te?e krystalove soustav?.

Sedm krystalografickych soustav uzce souvisi s krystalovymi m?i?kami a elementarnimi bu?kami . V?echny mo?nosti krystalove m?i?ky popisuje 14 Bravaisovych m?i?ek a z nich sedm odpovida sedmi krystalografickym soustavam.

Na rozdil od krystalickych latek nemaji amorfni latky uspo?adane struktury, jejich atomy nebo molekuly tvo?i nepravidelny vzor a nelze je za?adit do ?adne krystalograficke soustavy.

Historie [ editovat | editovat zdroj ]

Na konci 18. stoleti Rene Just Hauy publikoval svou teorii struktury krystal? z nejmen?ich stavebnich celk? ( Molecules constituantes ), co? lze pova?ovat za za?atek krystalografie.

Christian Samuel Weiss (1780?1856) p?elo?il Hauyovy u?ebnice a ji? v prvnim vydani sveho p?ekladu za?adil dodatek s nazvem Dynamicke pohledy na krystalizaci . Jeho nazor, ?e vn?j?i tvar krystal? by m?l byt chapan jako vyraz systemu vnit?nich sil, vedl k my?lence popsat uspo?adani zvla?t? napadnych sm?r? krystal? - tedy podel os . Osu definoval takto: Osa je p?imka, ktera dominuje celemu objektu a kolem ni? je v?e rovnom?rn? rozlo?eno. Toto rovnom?rne rozlo?eni kolem osy ji? nazna?ilo my?lenku rota?ni symetrie, ale teprve pozd?ji ji konkretn? formulovali Moritz Ludwig Frankenheim a Johann Friedrich Christian Hessel .

Christian Samuel Weiss tak do krystalografie zavedl osove systemy. Tvrdil, ?e prost?ednictvim pravouhlych krystalovych system?, ktere navrhl, lze popsat polohu ka?deho povrchu a ka?deho sm?ru. Podle uspo?adani os rozli?il celkem ?est krystalovych system?. S pomoci os byl Weiss poprve schopen charakterizovat polohu v?ech krystalovych ploch ?isly (indexy) ve tvaru:

ma : nb : pc ,

kde

a, b, c jsou delky hran,

m, n, p jsou pr?se?iky, kde p?islu?na plocha protina osy - Weissovy koeficienty

Ziskal tak nasledujici systemy (sou?asne ozna?eni v zavorkach):

Pravidelny (krychlovy) system: a = b = c, α = β = γ = 90°
?ty?dilny (?tvercovy) system: a = b ≠ c, α = β = γ = 90°
Dvoustup?ovy system: a, b, c r?zne ve dvojicich, α = β = γ = 90°
- Dvoustup?ovy a dvoustup?ovy (koso?tvere?ny) system
- Dvoustup?ovy a jednostup?ovy (jednoklonny) system
- Jednostup?ovy a jednostup?ovy (trojklonny) system
T?i?lenny nebo ?esti?lenny (klencovy/?estere?ny) system: t?i stejne osy se protinaji v uhlu 60° a ?tvrta nestejna osa v uhlu 90°

V letech 1812?1814 vyvinul Friedrich Mohs sv?j koncept krystalovych system?. Rozd?lil je na ?ty?i systemy ( koso?tvere?ny, pyramidalni, prizmaticky a tessularni ). Byl to Mohs?v ?ak Carl Friedrich Naumann , stejn? jako Moritz Ludwig Frankenheim a Justus Gunther Graßmann , kte?i pozd?ji vytvo?ili ?ikme osove systemy.

A? v roce 1848 vypracoval Traugott Leberecht Hasse historicky p?ehled krystalovych soustav v ortogonalnim popisu, tedy pomoci pravouhlych sou?adnic.

V roce 1866 Auguste Bravaise rozli?il sedm t?id symetrickych spojeni, ji? ne na zaklad? axialnich pom?r?, ale na zaklad? maximalnich kombinovatelnych rota?nich os . Tato klasifikace p?esn? odpovida sedmi modernim krystalografickym soustavam:

kubicka soustava: 3 ?ty?nasobne, 4 trojnasobne, 6 dvojite osy ota?eni
?estihranna soustava: 1 ?estinasobna, 6 dvojitych os ota?eni
tetragonalni soustava: 1 ?ty?stranne, 4 dvouk?idle osy ota?eni
trigonalni soustava: 1 trojite, 3 dvojite osy ota?eni
ortorombicka soustava: 3 dvojite osy rotace
monoklinicka soustava: 1 dvojita osa rotace
triklinicka soustava: bez os rotace

Krystalova soum?rnost [ editovat | editovat zdroj ]

Vyznamnou vlastnosti krystal? je pravidelnost polohy a vzajemneho uspo?adani jednotlivych ploch, ktera se nazyva krystalova soum?rnost. Rozli?ujeme t?i prvky soum?rnosti:

Rovina soum?rnosti rozd?luje krystal na dv? symetricke poloviny tak, ?e se jedna polovina kryje se zrcadlovym obrazem druhe poloviny.
P?iklad osove soum?rnosti
Osa soum?rnosti je my?lena p?imka vedena st?edem krystalu. P?i ota?eni kolem teto osy o 360 ^o se krystal op?tovn? dostava do polohy shodne s vychozi polohou. Podle toho, kolikrat se p?i plnem oto?eni docili shoda s vychozi polohou, rozeznavame osy dvoj, troj, ?ty? a ?esti?etne soum?rnosti.
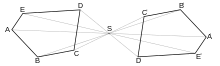P?iklad st?edove soum?rnosti
St?ed soum?rnosti ( bodove symetrie) krystalu je my?leny bod, kolem ktereho se krystal oto?i o 180 ^o a ka?de jeho plo?e pak odpovida shodna a rovnob??na plocha prot?j?i.

Kombinaci v?ech uvedenych prvk? soum?rnosti podle jejich po?tu a druhu m??eme za?adit v?echny krystaly do n?ktereho krystalografickeho odd?leni. Nelze je kombinovat libovoln?, nebo? jsou vzajemn? zavisle, tak?e po?et kombinaci je omezeny.

Existuje 230 kombinaci prvk? soum?rnosti, ktere se nazyvaji grupy symetrie . Z nich lze vybrat 32 skupin, ktere se ozna?uji jako krystalograficka odd?leni soum?rnosti - bodove grupy. Tato odd?leni soum?rnosti pak m??eme podle spole?nych znak? rozd?lit do 7 v?t?ich skupin - krystalografickych soustav.

Spole?nym znakem jednotlivych krystalografickych soustav je krystalograficky osni k?i? (trojrozm?rny sou?adnicovy system), ktery umo??uje p?esne ur?eni ka?de krystalove plochy. V?echny krystalove m?i?ky, krystalove struktury a krystaly, ktere mohou byt definovany stejnym trojrozm?rnym sou?adnicovym systemem, pat?i te?e krystalove soustav?.

Krystalova m?i?ka a elementarni bu?ka [ editovat | editovat zdroj ]

Krystalova m?i?ka je mno?ina ur?itych my?lenych abstraktnich bod?, pomoci nich? se popisuje struktura krystalu , neboli vzajemna poloha ?astic v krystalu .

V krystalove m?i?ce se v trojrozm?rnem prostoru kombinuji prvky st?edove soum?rnosti (bodove symetrie) a translace . Ka?dy typ krystalove m?i?ky je definovan t?emi vektory a, b, c . Orientace krystalove m?i?ky se obvykle provadi tak, aby sm?ry os soum?rnosti ( x, y, z ) byly paralelni s vektory a, b, c nebo krystalografickymi osami.

Podjednotkou krystalove m?i?ky je elementarni bu?ka . Je to rovnob??nost?n opakujici se podel hlavnich sm?r? trojrozm?rneho prostoru. Zakladni vektory ( a, b, c ) jsou definovany hranami zakladni bu?ky a jejich delky jsou zakladni periody m?i?ky. Spole?n? se t?emi uhly ( α, β, γ ), ktere zakladni vektory sviraji, tvo?i t?chto ?est hodnot m?i?kove parametry.

Podle vektor? a, b, c a uhl? α, β, γ mezi nimi se krystalove m?i?ky rozd?luji na:

triklinicka (trojklonna), a ₀ ≠ b ₀ ≠ c ₀, α ≠ β ≠ γ ≠ 90 ^o
monoklinicka (jednoklonna), a ₀ ≠ b ₀ ≠ c ₀, α = γ, β > 90°
rombicka (koso?tvere?na), a ₀ ≠ b ₀ ≠ c ₀, α = β = γ = 90°
tetragonalni (?tvere?na), a ₀ = b ₀ ≠ c ₀, α = β = γ = 90°
trigonalni (klencova), a ₀ = b ₀ = c ₀, (α = β = γ) ≠ 90°
hexagonalni (?estere?na), a ₀ = b ₀ ≠ c ₀ resp. a ₁ = a ₂ = a ₃ ≠ c ₀, α = β = 90°, γ = 120°
kubicka (krychlova), a = b = c, α = β = γ = 90°

Srovnani krystalografickych soustav, Bravaisovych m?i?ek a krystalovych m?i?ek [ editovat | editovat zdroj ]

Krystalograficka soustava	Po?adovana symetrie	Bravaisova m?i?ka	Krystalova m?i?ka
Trojklonna	?adna	1	Trojklonna
Jednoklonna	1 dvojnasobna osa ota?eni nebo 1 rovina soum?rnosti	2	Jednoklonna
Koso?tvere?na	3 dvojnasobne osy ota?eni nebo 1 dvojnasobna osa ota?eni a 2 roviny soum?rnosti	4	Koso?tvere?na
?tvere?na	1 ?ty?nasobna osa ota?eni	2	?tvere?na
Klencova	1 trojnasobna osa ota?eni	1	Klencova
Klencova	1 trojnasobna osa ota?eni	1	?estere?na
?estere?na	1 ?estinasobna osa ota?eni	1	?estere?na
Krychlova	4 trojnasobne osy ota?eni	3	Krychlova
Celkem 7		Celkem 14	Celkem 7

Jednoklonna
Trojklonna
Koso?tvere?na
?tvere?na
?estere?na
Klencova
Krychlova

Jednotlive krystalograficke soustavy [ editovat | editovat zdroj ]

Trojklonna (triklinicka) [ editovat | editovat zdroj ]

V?echny osy osoveho k?i?e jsou r?zn? dlouhe a sviraji libovolny kosy uhel.

Pro m?i?kove parametry plati:

a ₀ ≠ b ₀ ≠ c ₀, α ≠ β ≠ γ ≠ 90 ^o

Mineraly trojklonne soustavy:

albit ( ?ivec sodnovapenaty), chalkantit (modra skalice), kaolinit , plagioklas

Jednoklonna (monoklinicka) [ editovat | editovat zdroj ]

V?echny t?i osy osoveho k?i?e jsou nestejn? dlouhe, dv? osy spolu sviraji pravy uhel a t?eti osa s nimi svira libovolny kosy uhel.

Pro m?i?kove parametry plati:

a ₀ ≠ b ₀ ≠ c ₀, α = γ, β > 90°

Mineraly jednoklonne soustavy:

amfibol , augit , biotit , epidot , mastek , muskovit , ortoklas , sadrovec , staurolit

Koso?tvere?na (ortorombicka) [ editovat | editovat zdroj ]

V?echny t?i osy osoveho k?i?e jsou r?zn? dlouhe a jsou na sebe kolme.

Pro m?i?kove parametry plati:

a ₀ ≠ b ₀ ≠ c ₀, α = β = γ = 90°

Mineraly koso?tvere?ne soustavy:

antimonit , aragonit , baryt , markazit , olivin , sira , topaz

?tvere?na (tetragonalni) [ editovat | editovat zdroj ]

Dv? osy osoveho k?i?e jsou stejn? dlouhe, 1 nestejn? dlouha, v?echny 3 osy jsou kolme.

Pro m?i?kove parametry plati:

a ₀ = b ₀ ≠ c ₀, α = β = γ = 90°

Mineraly ?tvere?ne soustavy:

chalkopyrit , kasiterit , rutil

?estere?na (hexagonalni) [ editovat | editovat zdroj ]

?est stejn? dlouhych os osoveho k?i?e (t?i hlavni a t?i vedlej?i) le?i v jedne rovin? a sviraji mezi sebou uhel 60°, sedma osa stoji kolmo k teto rovin? a je nestejn? dlouha. Ma 7 rovin soum?rnosti.

Pro m?i?kove parametry plati:

a ₀ = b ₀ ≠ c ₀ resp. a ₁ = a ₂ = a ₃ ≠ c ₀, α = β = 90°, γ = 120°

Mineraly ?estere?ne soustavy:

apatit , beryl , grafit

Klencova (trigonalni) [ editovat | editovat zdroj ]

Klencova soustava byva n?kdy pro zjednodu?eni ?azena do ?estere?ne soustavy. Tyto soustavy maji stejny typ osniho k?i?e a li?i se ?etnosti svisle osy. T?i stejn? dlouhe osy osoveho k?i?e le?i v jedne rovin? a sviraji uhel 120°. ?tvrta osa stoji kolmo k teto rovin? a je stejn? dlouha.

Pro m?i?kove parametry plati:

a ₀ = b ₀ = c ₀, (α = β = γ) ≠ 90°

Mineraly klencove soustavy:

kalcit , korund , k?emen , magnezit , siderit , turmalin , hematit

Krychlova (kubicka) [ editovat | editovat zdroj ]

Krystaly krychlove soustavy maji nejvice rovin soum?rnosti (9). Na krystalech se ?asto uplat?uje krychle, osmist?n, dvanactist?n koso?tvere?ny nebo dvanactist?n p?tiuhelnikovy. Najdeme zde i tvar s nejv?t?im po?tem ploch (48st?n) a r?zne typy 24st?n?. V horninach mivaji zrna krychlovych mineral? kruhovity pr??ez (nap?iklad granat). Osni k?i? krychlove soustavy je tvo?en t?emi osami, ktere jsou na sebe kolme a v?echny jsou stejn? dlouhe.

Pro m?i?kove parametry plati:

a = b = c, α = β = γ = 90°

Mineraly krychlove soustavy:

diamant , fluorit , galenit , granat , halit (s?l kamenna), m?? , pyrit , sfalerit , st?ibro , zlato