Guyou hemisphere-in-a-square projection

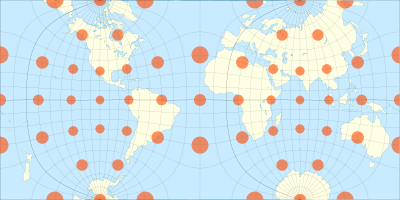The Guyou hemisphere-in-a-square projection is a conformal map projection for the hemisphere. It is an oblique aspect of the Peirce quincuncial projection .

History [ edit ]

The projection was developed by Emile Guyou  [ fr ] of France in 1887. ^{[1] [2]}

Formal description [ edit ]

The projection can be computed as an oblique aspect of the Peirce quincuncial projection by rotating the axis 45 degrees. It can also be computed by rotating the coordinates −45 degrees before computing the stereographic projection; this projection is then remapped into a square whose coordinates are then rotated 45 degrees. ^[3]

The projection is conformal except for the four corners of each hemisphere's square. Like other conformal polygonal projections, the Guyou is a Schwarz?Christoffel mapping .

Properties [ edit ]

Its properties are very similar to those of the Peirce quincuncial projection :

• Each hemisphere is represented as a square, the sphere as a rectangle of aspect ratio 2:1.
• The part where the exaggeration of scale amounts to double that at the centre of each square is only 9% of the area of the sphere, against 13% for the Mercator and 50% for the stereographic ^[4]
• The curvature of lines representing great circles is, in every case, very slight, over the greater part of their length. ^[4]
• It is conformal everywhere except at the corners of the square that corresponds to each hemisphere, where two meridians change direction abruptly twice each; the Equator is represented by a horizontal line.
• It can be tessellated in all directions.

Related projections [ edit ]

• The Adams hemisphere-in-a-square projection and the Peirce quincuncial projection are different aspects of the same underlying Schwarz?Christoffel mapping. Such mappings are transformations of half a stereographic projection .

See also [ edit ]

• List of map projections

References [ edit ]