Area
ar en storhet som beskriver utstrackningen av en
tvadimensionell
yta
i
planet
. Arean hos en form kan matas genom att jamfora den med en
kvadrat
av bestamd storlek.
SI-enheten
for area ar
kvadratmeter
(m²). Inom
matematiken
ar
enhetskvadraten
definierad till att ha arean 1. Ibland anvands
yta
som synonym till area (men jamfor artikeln
yta
). Nar man talar om arean hos landomraden anvands ibland
areal
.
[
1
]
Det finns flera valkanda formler som beskriver arean hos enkla
geometriska former
, sasom
trianglar
,
rektanglar
och
cirklar
. Med dessa formler kan arean av en godtycklig
polygon
beraknas med
polygontriangulering
, det vill saga att dela upp polygonen i trianglar.
[
2
]
For geometriska former med krokta
rander
maste man vanligen anvanda
matematisk analys
for att berakna arean. Faktum ar att behovet att kunna bestamma arean hos plana geometriska former var en av anledningarna till att den matematiska analysen utvecklades.
[
3
]
Ytarean hos enkla
tredimensionella
geometriska former sasom
sfarer
,
koner
och
cylindrar
kunde redan de gamla grekerna bestamma. Mer komplicerade kroppars ytarea kan beraknas med matematisk analys i flera variabler.
Area har stor betydelse inom modern matematik. Detta galler inte bara den uppenbara betydelsen inom
geometri
och matematisk analys; area ar beslaktat med definitionen av
determinanter
i
linjar algebra
, och ar en grundlaggande egenskap i
differentialgeometri
.
[
4
]
En ansats att definiera vad som menas med area ar genom ett antal
axiom
. Till exempel kan vi definiera area som en funktion
a
fran en samling speciella plana figurer (benamns matbara mangder)
M
till mangden reella tal som har foljande egenskaper:
- a
(
S
) ≥ 0 for alla
S
i
M
.
- Om
S
och
T
tillhor
M
sa gor aven
S
∪
T
,
S
∩
T
det och
a
(
S
∪
T
) =
a
(
S
) +
a
(
T
) -
a
(
S
∩
T
)
.
- Om
S
och
T
tillhor
M
med
S
⊆
T
sa tillhor
T
-
S
ocksa
M
och
a
(
T
-
S
) =
a
(
T
) -
a
(
S
)
.
- Om en mangd
S
tillhor
M
och
S
ar kongruent med
T
sa tillhor
T
ocksa
M
och
a
(
S
) =
a
(
T
).
- Varje rektangel
R
tillhor
M
. Om rektangeln har langden
h
och bredden
k
sa ar
a
(
R
) =
hk
.
- Lat
Q
vara en mangd innesluten mellan tva rektangelomraden
S
och
T
. Ett rektangelomrade utgors av en finit union av narliggande rektanglar pa en gemensam bas, det vill saga
S ⊆ Q ⊆ T
. Om det finns ett unikt tal
c
sadant att
a
(
S
) ≤ c ≤
a
(
T
)
for alla sadana rektangelomraden
S
och
T
, sa ar
a
(
Q
) =
c
.
 En
kvadrat
med ytan en kvadratmeter.
En
kvadrat
med ytan en kvadratmeter.
Varje
langdenhet
har en motsvarande
ytenhet
, dar langdenheten motsvarar alla sidor i en kvadrat. Alltsa kan area matas i till exempel kvadratmeter (m²), kvadratcentimeter (cm²), kvadratmillimeter (mm²), kvadratkilometer (km²).
 Det gar 10 mm pa 1 cm, och 100 mm² pa 1 cm².
Det gar 10 mm pa 1 cm, och 100 mm² pa 1 cm².
Omvandlingar mellan tva ytenheter ar kvadraten av deras langdforhallande. Till exempel ar
- 1
cm
= 10
mm
och forhallandet mellan cm² och mm² ar 100, det vill saga 10
2
.
Vidare ar:
- 1 kvadratkilometer =
1 000 000
kvadratmeter
- 1 kvadratmeter = 10 000 kvadratcentimeter = 1 000 000 kvadratmillimeter
Det finns flera andra vanliga enheter for area.
Aret
var den forsta enheten i det metriska mattsystemet, dar
Aven om ar sallan anvands idag anvands
hektar
fortfarande vanligen som enhet for markarea.
- 1 hektar = 100 ar = 10 000 kvadratmeter = 0,01 kvadratkilometer.
 Arean hos den har rektangeln ar
l
×
w
.
Arean hos den har rektangeln ar
l
×
w
.
Den enklaste areaformeln ar
rektangeln
. Givet en rektangel med langden
l
och bredden
b
, ar arean
 (rektangel)
(rektangel)
Alltsa, arean hos en rektangel ar langden
multiplicerat
med bredden. Som ett specialfall av detta har en kvadrat med sidolangd
s
arean
 (kvadrat)
(kvadrat)
Formeln for arean hos en rektangel foljer direkt fran de grundlaggande egenskaperna hos area, och betraktas ibland som en
definition
eller ett
axiom
. A andra sidan, om
geometri
utvecklas fore
aritmetik
, kan denna formel anvandas for att definiera multiplikation av
reella tal
.
 Figurer med samma area.
Figurer med samma area.
De flesta andra enkla formlerna for area foljer av
dissektion
. Detta innebar att man skar en plan figur i bitar, som
summerar
till arean hos originalfiguren.
Till exempel kan alla
parallellogram
delas upp i en
trapetsoid
och en rat
triangel
(enligt figuren till vanster). Om triangeln flyttas till andra sidan av trapetsoiden resulterar detta i en rektangel. Darfor ar arena hos en parallellogram samma som for en rektangel:
 (parallellogram)
(parallellogram)
 Tva kongruenta trianglar.
Tva kongruenta trianglar.
Men samma parallellogram kan ocksa skaras langs sin ena
diagonal
till tva
kongruenta
trianglar, som i figuren till hoger. Fran detta far man att arean hos vardera triangel ar halften av arean hos parallellogrammet:
 (triangel)
(triangel)
Liknande resonemang kan foras for att hitta formler for arean hos
trapetsoider
,
romber
och mer avancerade
polygoner
.
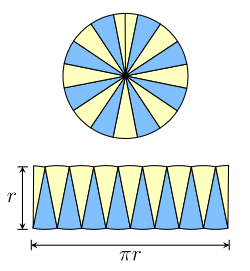 En cirkel kan delas upp i
cirkelsektorer
, som ungefarligen kan arrangeras som en parallellogram.
En cirkel kan delas upp i
cirkelsektorer
, som ungefarligen kan arrangeras som en parallellogram.
Formeln for
cirkelns
area grundar sig i en liknande metod. Givet en cirkel med radien
r
kan den delas in i sektorer enligt figuren till hoger. Varje sektor ar
approximativt
en triangular, och kan fordelas om till en approximativ parallellogram. Hojden hos denna parallellogram ar
r
och bredden halften av omkretsen hos cirkeln, eller π
r
. Alltsa ar den totala arean hos cirkeln
r
?π
r
eller π?
r
2
.
 (cirkel)
(cirkel)
Trots att dissektionen av cirkeln till sektorer ar approximativ blir felet mindre och mindre, ju fler sektorer som cirkeln delas in i.
Gransvardet
som arean hos parallellogrammen gar mot ar exakt π?
r
2
, som ar cirkelns area. Detta resonemang ar en enkel tillampning av
matematisk analys
.
 Arkimedes
visade att mantelarean och volymen hos en
sfar
ar exakt ⅔ av arean och volymen hos den omkringliggande
cylindriska ytan
.
Arkimedes
visade att mantelarean och volymen hos en
sfar
ar exakt ⅔ av arean och volymen hos den omkringliggande
cylindriska ytan
.
De flesta enkla formler for mantelarea kan fas genom att skara upp ytan och slata ut till ett plan. Till exempel, om sidan hos en
cylinder
eller ett
prisma
skars pa langden kan ytan slatas ut till en rektangel. Pa samma satt, om en
kon
skars fran basen till toppen kan ytan slatas ut till en cirkelsektor, och arean raknas ut.
Formeln for mantelarean hos en
sfar
ar svarare: eftersom ytan pa en sfar har
Gausskrokning
som ar skild fran noll kan den inte slatas ut till ett plan. Mantelarean hos en sfar beraknades forst av
Arkimedes
i hans verk 'Om matning av cirkeln'. Formeln ar
 (sfar)
(sfar)
dar
r
ar radien hos sfaren. Precis som for cirkeln anvander harledningar av denna formel metoder som paminner om matematisk analys.
Vanliga areaformler
| Figur
|
Formel
|
Variabler
|
| Regelbunden
triangel
(
liksidig triangel
)
|

|
s
ar langden hos en sida i triangeln.
|
| Triangel
|

|
s
ar halva perimetern,
a
,
b
och
c
ar langderna hos sidorna.
|
| Triangel
|

|
a
och
b
ar tva av sidorna, och γ ar vinkeln mellan dem.
|
| Triangel
|

|
b
och
h
ar
basen
och hojden (matt vinkelratt basen).
|
| Kvadrat
|

|
s
ar langden hos en sida.
|
| Rektangel
|

|
l
och
b
ar langderna hos sidorna (langd och bredd).
|
| Romb
|

|
a
och
b
ar langderna hos de tva
diagonalerna
.
|
| Parallellogram
|

|
b
ar landgden hos basen och
h
har hojden vinkelratt mot basen.
|
| Parallelltrapets
|

|
a
och
b
ar de parallella sidornas langder och
h
avstandet (hojden) mellan de parallella sidorna.
|
| Regelbunden
hexagon
|

|
s
ar langden pa en sida hos hexagonen.
|
| Regelbunden
oktagon
|

|
s
ar langden pa en sida hos oktagonen.
|
| Regelbunden polygon
|

|
s
ar langden pa sidan, och
n
antalet sidor.
|

|
a
ar
apotemat
(radien hos en
inskriven cirkel
som tangerar polygonen) och
p
ar polygonens omkrets.
|
| Cirkel
|
 eller eller

|
r
ar radien, och
d
diametern
.
|
| Cirkelsektor
|

|
r
och
θ
ar radien och vinkeln i
radianer
.
|
| Ellips
|

|
a
och
b
ar halva langden av ellipsens storaxel respektive lillaxel.
|
| Total omslutningsarea (
begransningsarea
) hos en
Kub
|

|
s ar langden av kubens kant.
|
| Total omslutningsarea (begransningsarea) hos ett
Ratblock
|

|
a, b och c ar langden av ratblockets kanter.
|
| Total omslutningsarea (begransningsarea) hos en
Cylinder
|

|
 och och
 ar radien och hojden. ar radien och hojden.
|
| Mantelarea hos en cylinder
|

|
r
och
h
ar radien och hojden.
|
| Total omslutningsarea (begransningsarea) hos en
kon
|

|
r
och
l
ar radien och langden fran basperiferin till toppen.
|
| Mantelarea hos en kon
|

|
r
och
l
ar radien och langden fran basperiferin till toppen.
|
| Total ytarea hos en
sfar
|

|
r
och
d
ar radien och diametern.
|
| Total ytarea hos en regelbunden
Pyramid
|

|
B
ar basarean,
p
ar basens perimeter och
l
ar apotemat (det vinkelrata avstandet fran baspolygonens kanter till toppen).
|
| Konvertering fran
kvadratisk
till cirkular area
|

|
A
ar arean hos kvadraten i kvadratisk enhet.
|
| Konvertering fran
Cirkular
till kvadratisk area
|

|
C
ar arean hos cirkeln i cirkular enhet.
[
forklaring behovs
]
|
Formlerna ovan visar hur arean kan beraknas for manga enkla och regelbundna figurer. Arean hos oregelbundna polygoner kan beraknas med
koordinatareaformeln
.
[
5
]
- Den har artikeln ar helt eller delvis baserad pa material fran
Engelsksprakiga Wikipedia
.