Em matematica , uma cadeia de Markov (cadeia de Markov em tempo discreto ou DTMC ^{[ 1 ] [ 2 ] [ 3 ]} ) e um caso particular de processo estocastico com estados discretos (o parametro, em geral o tempo, pode ser discreto ou continuo) com a propriedade de que a distribuicao de probabilidade do proximo estado depende apenas do estado atual e nao na sequencia de eventos que precederam, uma propriedade chamada de Markoviana, chamada assim em homenagem ao matematico Andrei Andreyevich Markov . A definicao dessa propriedade, tambem chamada de memoria markoviana, e que os estados anteriores sao irrelevantes para a predicao dos estados seguintes, desde que o estado atual seja conhecido. Cadeias de Markov tem muitas aplicacoes como modelos estatisticos de processos do mundo real.

Introducao [ editar | editar codigo-fonte ]

A cadeia de Markov e um processo estocastico com a propriedade de Markov. ^{[ 4 ]} O termo "cadeia de Markov" refere-se a sequencia de variaveis aleatorias, tais um processo move-se atraves de, com a propriedade de Markov definindo a dependencia de serie unica entre periodos adjacentes (como em uma "cadeia"). Assim, pode ser usado para sistemas que seguem uma cadeia de eventos ligados, onde o que acontece em seguida depende apenas do estado atual do sistema descrevendo.

Na literatura, diferentes tipos de processo de Markov sao designados como "cadeia de Markov". Normalmente, o termo e reservado para um processo com um conjunto discreto de vezes, isto e, Cadeia de Markov de Tempo Discreto (DTMC). ^{[ 5 ]} Por outro lado, alguns autores utilizam o termo "processo de Markov" para se referir a uma cadeia de Markov de tempo continuo sem referencia explicita. ^{[ 6 ] [ 7 ]}

Enquanto o parametro de tempo e geralmente discreto, o espaco de estado de uma cadeia de Markov nao tem quaisquer restricoes geralmente aceitas: o termo pode referir-se a um processo em um espaco de estado arbitrario. ^{[ 8 ]} No entanto, muitas aplicacoes de Cadeias de Markov empregam conjuntos contaveis finitos ou infinitos (isto e, espacos de estado discretos), que tem uma analise estatistica mais simples. Alem da hora do indice e os parametros de espaco de estado, ha muitas outras variacoes, extensoes e generalizacoes (ver Variacoes). Para simplificar, a maior parte deste artigo concentra-se no tempo discreto, discreta caso de espaco de estado, salvo indicacao em contrario.

As mudancas de estado do sistema sao chamadas transicoes. As probabilidades associadas com varias mudancas de estado sao chamados de probabilidades de transicao. O processo e caracterizado por um espaco de estado, uma matriz de transicao descrevendo as probabilidades de transicoes de particulares, e um estado inicial (ou a distribuicao inicial) atraves do espaco de estado. Por convencao, assumimos todos os estados e transicoes possiveis foram incluidos na definicao do processo, por isso ha sempre um proximo estado, e o processo nao termina.

Um processo aleatorio de tempo discreto envolve um sistema que e em um determinado estado, em cada passo, com o estado a mudar de forma aleatoria entre os passos. Os passos sao muitas vezes considerados como momentos no tempo, mas podem igualmente bem se referirem a distancia fisica ou a qualquer outra medida discreta. Formalmente, os passos sao os numeros inteiros ou numeros naturais, e o processo aleatorio e um mapeamento destes para estados. A propriedade de Markov afirma que a distribuicao de probabilidade condicional para o sistema no proximo passo (e, de fato, em todas as etapas futuras) depende apenas do estado atual do sistema, e nao adicionalmente sobre o estado do sistema em etapas anteriores.

Uma vez que o sistema altera aleatoriamente, e geralmente impossivel prever com exatidao o estado de uma cadeia de Markov num dado momento no futuro. No entanto, as propriedades estatisticas do futuro do sistema podem ser previstas. Em muitas aplicacoes, sao elas as importantes.

A famosa cadeia de Markov e o chamado "andar do bebado", um passeio aleatorio na linha numero onde, a cada passo, a posicao pode mudar por um ou -1 com igual probabilidade. A partir de qualquer posicao ha duas transicoes possivel, para o seguinte ou anterior inteiro. As probabilidades de transicao dependem somente da posicao atual, nao sobre o modo em que a posicao foi alcancada. Por exemplo, as probabilidades de transicao de 5-4 e 5-6 sao ambos 0,5, e todos os outros a partir de probabilidades de transicao 5 e 0. Estas probabilidades sao independentes do fato de se o sistema foi anteriormente em 4 ou 6.

Outro exemplo sao os habitos alimentares de uma criatura que so come uvas, queijo ou alface, e cujos habitos alimentares estao em conformidade com as seguintes regras:

• Ele come apenas uma vez por dia.
• Se ele comeu queijo hoje, amanha ele vai comer alface ou uvas com igual probabilidade.
• Se ele comeu uvas hoje, amanha ele vai comer uvas com probabilidade de 1/10, queijo com probabilidade 4/10 e alface com probabilidade 5/10.
• Se ele comeu alface hoje, amanha ele vai comer uvas com probabilidade de 4/10 ou queijo com probabilidade 6/10. Ele nao vai comer alface novamente amanha.

Os habitos alimentares desta criatura podem ser modelados com uma cadeia de Markov desde que a escolha em seu amanha depende unicamente do que comer em seu hoje, e nao do que comeu ontem ou em qualquer outro momento do passado. Uma propriedade estatistica e de que a percentagem esperada pode ser calculada ao longo de um longo periodo de tempo, dos dias em que a criatura vai comer uvas.

Uma serie de eventos independentes (por exemplo, uma serie de arremessos de moedas) satisfaz a definicao formal de uma cadeia de Markov. No entanto, a teoria e normalmente aplicada apenas quando a distribuicao de probabilidade do proximo passo depende nao-trivialmente sobre o estado atual. Existem muitos outros exemplos de cadeias de Markov.

Definicao formal [ editar | editar codigo-fonte ]

Uma cadeia de Markov e uma sequencia X ₁ , X ₂ , X ₃ , ... de variaveis aleatorias . O escopo destas variaveis, isto e, o conjunto de valores que elas podem assumir, e chamado de espaco de estados , onde X _n denota o estado do processo no tempo n . Se a distribuicao de probabilidade condicional de X _{n +1} nos estados passados e uma funcao apenas de X _n , entao:

${\displaystyle \Pr(X_{n+1}=x|X_{0},X_{1},X_{2},\ldots ,X_{n})=\Pr(X_{n+1}=x|X_{n}),\,}$

onde x e algum estado do processo. A identidade acima define a propriedade de Markov .

Cadeias de Markov sao frequentemente descritas por uma sequencia de grafos dirigidos, onde as arestas do grafico n sao rotulados por as probabilidades de ir de um estado no tempo n para outros estados no tempo n+1 , ${\displaystyle \Pr(X_{n+1}=x\mid X_{n}=x_{n})}$. A mesma informacao e representada pela matriz de transicao de momento n para o tempo n+1 . No entanto, as cadeias Markov sao assumidas frequentemente como sendo tempo-homogeneas (ver variacoes abaixo), nesse caso o grafico e a matriz sao independentes de n e, portanto, nao sao apresentados como sequencias.

Estas descricoes realcam a estrutura da cadeia de Markov que e independente da distribuicao inicial ${\displaystyle \Pr(X_{1}=x_{1})}$. Quando o tempo e homogeneo, a cadeia pode ser interpretada como uma maquina de estado atribuindo uma probabilidade de pular de cada vertice ou estado para outro adjacente. A probabilidade ${\displaystyle \Pr(X_{n}=x|X_{1}=x_{1})}$ de Estado da maquina pode ser analisado como o comportamento estatistico da maquina com um elemento ${\displaystyle x_{1}}$ do espaco de estados como entrada, ou como o comportamento da maquina com a distribuicao inicial ${\displaystyle \Pr(X_{1}=y)=[x_{1}=y]}$ de estados como entrada, onde ${\displaystyle [P]}$ e o suporte de Iverson.

O fato de que algumas sequencias de estados pode ter zero probabilidade de ocorrencia corresponde a um grafico com varios componentes ligados, onde se omitem arestas que levaria a uma probabilidade de transicao zero. Por exemplo, se a tem uma probabilidade diferente de zero de ir para b , mas a e x estao em diferentes componentes ligados do grafico, entao, ${\displaystyle \Pr(X_{n+1}=b|X_{n}=a)}$ e definida, enquanto ${\displaystyle \Pr(X_{n+1}=b|X_{1}=x,...,X_{n}=a)}$ nao e.

Uma maneira simples de visualizar um tipo especifico de cadeia de Markov e atraves de uma maquina de estados finitos . Se voce esta no estado y no tempo n , entao a probabilidade de que voce se mova para o estado x no tempo n  + 1 nao depende de n , e somente depende do estado atual y em que voce esta. Assim em qualquer tempo n , uma cadeia de Markov finita pode ser caracterizada por uma matriz de probabilidades cujo elemento ( x , y ) e dado por ${\displaystyle \Pr(X_{n+1}=x|X_{n}=y)\,}$ e e independente do tempo n . Estes tipos de cadeia de Markov finitas e discretas podem tambem ser descritas por meio de um grafo dirigido (orientado), onde cada aresta e rotulada com as probabilidades de transicao de um estado a outro sendo estes estados representados como os nos conectados pelas arestas.

Caracterizacao de um processo de Markov [ editar | editar codigo-fonte ]

Um processo de Markov e um processo estocastico em que a probabilidade de o sistema estar no estado i no periodo (n+1) depende somente do estado em que o sistema esta no periodo n . Ou seja, para os processos de Markov, so interessa o estado imediato. ^{[ 9 ] [ 10 ]} Os principais elementos de um processo de Markov sao dois : ^{[ 9 ]}

• a probabilidade x ⁱ (n) de ocorrer o estado i no n-esimo periodo de tempo , ou, alternativamente, a fracao da populacao em questao que esta no estado i no n-esimo periodo de tempo
• as probabilidades de transicao m _ij , que representam as probabilidades de o processo estar no estado i no tempo (n+1) dado que esta no estado j no tempo n . Estas probabilidades de transicao sao normalmente agrupadas numa matriz, que denominamos matriz de transicao , matriz estocastica ou ainda matriz de Markov .

Variacoes [ editar | editar codigo-fonte ]

• Processos de Markov de tempo continuo tem um indice continuo.
• Cadeias de Markov de tempo homogeneo (ou cadeias de Markov estacionarias) sao processos em que

${\displaystyle \Pr(X_{n+1}=x\mid X_{n}=y)=\Pr(X_{n}=x\mid X_{n-1}=y)\,}$

para todo n . A probabilidade da transicao de n e independente.

• Uma cadeia de Markov de ordem m (ou uma cadeia de Markov com memoria m ), onde m e finito, e um processo que satisfaca

${\displaystyle {\begin{aligned}{}&\Pr(X_{n}=x_{n}\mid X_{n-1}=x_{n-1},X_{n-2}=x_{n-2},\dots ,X_{1}=x_{1})\\=&\Pr(X_{n}=x_{n}\mid X_{n-1}=x_{n-1},X_{n-2}=x_{n-2},\dots ,X_{n-m}=x_{n-m}){\text{ para }}n>m\end{aligned}}}$

Em outras palavras, o estado futuro depende dos passados ${\displaystyle m}$ estados. E possivel construir uma cadeia ${\displaystyle (Y_{n})}$ de ${\displaystyle (X_{n})}$, que tem a propriedade de Markov "classico", tendo como espaco de estado do ${\displaystyle m}$-tuplas ordenadas de valores ${\displaystyle X}$, ou seja, ${\displaystyle Y_{n}=(X_{n},X_{n-1},\dots ,X_{n-m+1})}$.

Cadeias de Markov em espacos de estados discretos [ editar | editar codigo-fonte ]

Um espaco de estados e representavel por uma matriz . Chamada de matriz de transicao , com o ( i , j )-esimo elemento igual a

${\displaystyle P_{ij}=\Pr(X_{n+1}=j\mid X_{n}=i)\,}$

Para um espaco de estados discretos, as integracoes na probabilidade de transicao de k passos sao somatorios, e podem ser calculados como a k -esima potencia da matriz de transicao. Isto e, se P e a matriz de transicao para um passo, entao P ^k e a matriz de transicao para a transicao de k passos.

A distribuicao estacionaria ${\displaystyle \pi }$ e o vetor que satisfaz a equacao :

${\displaystyle \pi ^{T}\mathbf {P} =\pi ^{T},}$

onde ${\displaystyle \pi ^{T}}$ e o vetor transposto de ${\displaystyle \pi }$. Em outras palavras, a distribuicao estacionaria ${\displaystyle \pi }$ e o autovetor (vetor proprio) esquerdo da matriz de transicao, associado com o autovalor (valor proprio) 1.

Como consequencia, nem a existencia nem a unicidade de distribuicao estacionaria e garantida para uma matriz de transicao qualquer P . Contudo, se P e irredutivel e aperiodica, entao existe uma distribuicao estacionaria ${\displaystyle \pi }$. Alem disso, P ^k converge para uma matriz na qual cada linha e a (transposta da) distribuicao estacionaria ${\displaystyle \pi ^{T}}$, que e dada por:

${\displaystyle \lim _{k\rightarrow \infty }\mathbf {P} ^{k}=\mathbf {1} \pi ^{T},}$

onde ${\displaystyle \mathbf {1} }$ e o vetor coluna com todas as entradas iguais a 1. Isto e estabelecido pelo Teorema de Perron-Frobenius .

Isto significa que se nos simularmos ou observamos uma caminhada aleatoria com matriz de transicao P , entao a probabilidade de longo prazo de que o individuo que faz a caminhada esteja em um certo estado e independente do estado em que essa caminhada comecou, e e definida pela distribuicao estacionaria. A caminhada aleatoria "ignora" o passado. Em suma, cadeias de Markov sao o passo seguinte depois dos processos sem memoria (isto e, uma sequencia de variaveis aleatorias independentes distribuidas uniformemente).

Uma matriz de transicao que e positiva (isto e, todo o elemento da matriz e positivo) e irredutivel e aperiodica. Uma matriz e uma matriz estocastica se e somente se e uma matriz de probabilidades de transicao de uma cadeia de Markov.

Um caso especial de probabilidade de transicao independente do passado e conhecido como o esquema de Bernoulli . Um esquema de Bernoulli com somente dois estados possiveis e conhecido como um processo de Bernoulli .

Exemplo [ editar | editar codigo-fonte ]

Um diagrama de estado para um exemplo simples e mostrado na figura a direita, usando para imaginar as transicoes de estado de um grafo dirigido. Os estados representam se um mercado de acoes hipotetico esta exibindo um mercado em alta, mercado em baixa, ou tendencia do mercado estagnado durante uma determinada semana. De acordo com a figura, uma semana de alta e seguido por uma outra semana de alta 90% do tempo, de uma semana de baixa 7,5% do tempo, e uma semana estagnada outro 2,5% do tempo. Etiquetas de espaco de estado {1 = alta, 2 = baixa, 3 = estagnado} a matriz de transicao para este exemplo e

${\displaystyle P={\begin{bmatrix}0.9&0.075&0.025\\0.15&0.8&0.05\\0.25&0.25&0.5\end{bmatrix}}.}$

A distribuicao por estados pode ser escrito como um vetor de linha estocastico x com x ^{( n  + 1)}  =  x ^{( n )} P . Assim, se no tempo n o sistema esta no estado x ^{( n )} , e em seguida, tres periodos de tempo mais tarde, no tempo n  + 3 a distribuicao e

${\displaystyle {\begin{aligned}x^{(n+3)}&=x^{(n+2)}P=\left(x^{(n+1)}P\right)P\\\\&=x^{(n+1)}P^{2}=\left(x^{(n)}P\right)P^{2}\\&=x^{(n)}P^{3}\\\end{aligned}}}$

Em particular, se num momento n o sistema esta no estado 2 (baixa), entao no tempo n  + 3 , a distribuicao e

${\displaystyle {\begin{aligned}x^{(n+3)}&={\begin{bmatrix}0&1&0\end{bmatrix}}{\begin{bmatrix}0.9&0.075&0.025\\0.15&0.8&0.05\\0.25&0.25&0.5\end{bmatrix}}^{3}\\&={\begin{bmatrix}0&1&0\end{bmatrix}}{\begin{bmatrix}0.7745&0.17875&0.04675\\0.3575&0.56825&0.07425\\0.4675&0.37125&0.16125\\\end{bmatrix}}\\&={\begin{bmatrix}0.3575&0.56825&0.07425\end{bmatrix}}.\end{aligned}}}$

Utilizando a matriz de transicao, e possivel calcular, por exemplo, a fraccao de longo prazo de semanas durante o qual o mercado e estagnado, ou o numero medio de semanas que sera necessario para passar de uma estagnada a um mercado de touro. Usando as probabilidades de transicao, as probabilidades de estado estacionario indicam que 62,5% das semanas estara em um mercado de touro, 31,25% de semanas estara em um mercado de urso e 6,25% de semanas sera estagnada, uma vez que:

${\displaystyle \lim _{N\to \infty }\,P^{N}={\begin{bmatrix}0.625&0.3125&0.0625\\0.625&0.3125&0.0625\\0.625&0.3125&0.0625\\\end{bmatrix}}}$

Um desenvolvimento aprofundado e muitos exemplos podem ser encontradas na monografia sobre-linha Meyn & Tweedie 2005. ^{[ 11 ]}

Imagine um pais onde so seja possivel estar em tres classes sociais, denominadas estados: A, B ou C. Em cada periodo de tempo, a probabilidade de uma pessoa mudar de um estado para outro e constante no tempo e so depende dos estados. Este processo e chamado de cadeia de Markov. ^{[ 12 ]}

Uma maquina de estado finito pode ser utilizada como uma representacao de uma cadeia de Markov. Assumindo uma sequencia de sinais de entrada independentes e identicamente distribuidos (por exemplo, simbolos de um alfabeto binario escolhido por lancamentos de moeda), se a maquina esta no estado y no tempo n , entao a probabilidade de que ele se move para declarar x no tempo n  + 1 depende apenas do estado atual.

Evolucao transitoria [ editar | editar codigo-fonte ]

A probabilidade de ir do estado i para o estado j em intervalos de tempo n e

${\displaystyle p_{ij}^{(n)}=\Pr(X_{n}=j\mid X_{0}=i)\,}$

e a transicao de um unico passo e

${\displaystyle p_{ij}=\Pr(X_{1}=j\mid X_{0}=i).\,}$

Para uma cadeia de Markov de tempo homogeneo:

${\displaystyle p_{ij}^{(n)}=\Pr(X_{k+n}=j\mid X_{k}=i)\,}$

e

${\displaystyle p_{ij}=\Pr(X_{k+1}=j\mid X_{k}=i).\,}$

As probabilidades de transicao de n -etapa satisfazem a equacao Chapman-Kolmogorov, que para qualquer k tal que 0 <  k  <  n ,

${\displaystyle p_{ij}^{(n)}=\sum _{r\in S}p_{ir}^{(k)}p_{rj}^{(n-k)}}$

onde S e o espaco de estados da cadeia de Markov.

A distribuicao marginal Pr( X _n  =  x ) e a distribuicao mais estados no tempo n . A distribuicao inicial e Pr( X ₀  =  x ). A evolucao do processo atraves de um passo de tempo e descrita pela

${\displaystyle \Pr(X_{n}=j)=\sum _{r\in S}p_{rj}\Pr(X_{n-1}=r)=\sum _{r\in S}p_{rj}^{(n)}\Pr(X_{0}=r).}$

Nota: O expoente ( n ) e um indice e nao um expoente.

Propriedades [ editar | editar codigo-fonte ]

Redutibilidade [ editar | editar codigo-fonte ]

Um estado j e dito ser acessivel a partir de um estado i (escrito i  →  j ) se um sistema comecou no estado i tem uma probabilidade diferente de zero de transicao para o estado j em algum ponto. Formalmente, o estado j e acessivel a partir do estado i , se existe um inteiro n _ij  ≥ 0 tal que

${\displaystyle \Pr(X_{n_{ij}}=j\mid X_{0}=i)=p_{ij}^{(n_{ij})}>0.\,}$

Este inteiro e permitido para ser diferente para cada par de estados, portanto, os subscritos em n _ij . Permitindo que n seja zero significa que cada estado e definida para ser acessivel a partir de si mesmo.

Um estado i e dito para se comunicar com o estado j (escrito i  ↔  j ) se ambos i  →  j e j  →  i . Um conjunto de estados C e uma classe de comunicacao se cada par de estados em C comunica com o outro. Uma classe comunicacao esta fechado se a probabilidade de deixar a classe e zero, ou seja, que se i estiver em C , mas j nao, entao j nao e acessivel a partir de i . Pode-se mostrar que a comunicacao neste sentido e uma relacao de equivalencia e, assim, que as classes comunicantes sao as classes de equivalencia dessa relacao.

O conjunto de classes comunicantes forma, um grafico aciclico dirigido por herdar as setas do espaco estado original. Uma classe comunicacao esta fechado, se e somente se ele nao tem setas de saida neste grafico.

Um estado i e dito ser essencial ou final se para todo j tal que i  →  j tambem e verdade que j  →  i . Um estado i e nao-essencial se nao e essencial. ^{[ 13 ]} Um estado e definitiva se e somente se sua classe comunicacao esta fechado.

A cadeia de Markov e dito ser irredutivel se o seu espaco de estado e uma classe unica comunicacao; em outras palavras, se e possivel chegar a qualquer estado de qualquer estado.

Periodicidade [ editar | editar codigo-fonte ]

Um estado i tem periodo k se houver retorno ao estado i deve ocorrer em multiplos de passos de tempo k . Formalmente, o periodo de um estado e definido como

${\displaystyle k=mdc\{n>0:\Pr(X_{n}=i\mid X_{0}=i)>0\}}$

(Onde "mdc" e o maior divisor comum), desde que este conjunto nao e vazio. Caso contrario, o periodo nao esta definido. Note-se que mesmo que um estado tem periodo k , pode nao ser possivel atingir o estado em k passos. Por exemplo, suponha que e possivel voltar ao estado em {6, 8, 10, 12, ...} intervalos de tempo; k seria 2, embora 2 nao aparece nesta lista.

Se k = 1, entao o estado e dito ser aperiodico: retorno ao estado i pode ocorrer em periodos irregulares. Pode ser demonstrado que um estado i e aperiodico se e somente se existe n tal que para todo n' ≥ n ,

${\displaystyle \Pr(X_{n'}=i\mid X_{0}=i)>0.}$

Caso contrario ( k  > 1), o estado e dito ser periodico com periodo  k . A cadeia de Markov e aperiodica se cada estado e aperiodico. Uma cadeia de Markov irredutivel so precisa de um estado aperiodico para implicar que todos os estados sao aperiodicos.

Cada estado de um grafo bipartido tem um periodo regular.

Transitoriedade [ editar | editar codigo-fonte ]

Um estado i e dito transitorio, se, uma vez que comecamos no estado i , existe uma probabilidade nao nula de que nunca voltara a i . Formalmente, seja a variavel aleatoria T _i o primeiro tempo de retorno ao estado i (o "hitting time"):

${\displaystyle T_{i}=\inf\{n\geq 1:X_{n}=i\mid X_{0}=i\}.}$

O numero

${\displaystyle f_{ii}^{(n)}=\Pr(T_{i}=n)}$

e a probabilidade de voltar para o estado i pela primeira vez apos n passos. Portanto, o estado i e transitorio se

${\displaystyle \Pr(T_{i}<{\infty })=\sum _{n=1}^{\infty }f_{ii}^{(n)}<1.}$

O estado i e recorrente (ou persistente) se nao e transitorio. Estados recorrentes tem garantidos (com probabilidade 1) um hitting time finito. Recorrencia e transitoriedade sao propriedades de classe, isto e, elas sao validas ou nao de forma igual para todos os membros de uma classe comunicante.

Tempo medio de recorrencia [ editar | editar codigo-fonte ]

Mesmo que o hitting time seja finito com probabilidade 1, ele nao precisa de ter uma expectativa finita. O tempo de recorrencia media no estado i e o tempo de retorno esperado M _i :

${\displaystyle M_{i}=E[T_{i}]=\sum _{n=1}^{\infty }n\cdot f_{ii}^{(n)}.\,}$

Estado i e recorrente positivo (ou persistente nao-nulo) se M _i e finito; caso contrario, o estado i e recorrente nulo (ou persistente nulo).

Numero esperado de visitas [ editar | editar codigo-fonte ]

Pode ser mostrado que um estado i e recorrente se e somente se o numero esperado de visitas a este estado e infinito, isto e,

${\displaystyle \sum _{n=0}^{\infty }p_{ii}^{(n)}=\infty .}$

Absorvendo estados [ editar | editar codigo-fonte ]

Um estado i e chamado de absorcao, se e impossivel sair deste estado. Portanto, o estado i esta absorvendo se e somente se

${\displaystyle p_{ii}=1{\text{ and }}p_{ij}=0{\text{ for }}i\not =j.}$

Se cada estado pode chegar a um estado de absorcao, entao a cadeia de Markov e uma cadeia de Markov absorvente.

Ergodicidade [ editar | editar codigo-fonte ]

Um estado i e dito ser ergodico se ele tem uma recorrencia aperiodica e positiva. Em outras palavras, um estado i e ergodico se for recorrente, tem um periodo de 1 e tem tempo de recorrencia media finita. Se todos os estados em uma cadeia de Markov irredutivel sao ergodicos, entao a cadeia e ergodica.

E possivel mostrar que uma cadeia de Marvok irredutivel de estado finito e ergodica se ela tem um estado aperiodico. A cadeia de Markov tem a propriedade ergodica se ha um numero finito N tal que qualquer estado pode ser alcancado a partir de qualquer outro estado em exatamente N passos. No caso de uma matriz de transicao totalmente ligada, em que todas as transicoes tem uma probabilidade nao nula, esta condicao e preenchida com N = 1. A cadeia de Markov com mais de um estado e apenas uma transicao de sair por estado nao pode ser ergodica.

Analise de estado estacionario e distribuicoes limitantes [ editar | editar codigo-fonte ]

Se a cadeia de Markov e uma cadeia de Markov de tempo homogenea, de modo que o processo e descrito por uma unica matriz que independe do tempo ${\displaystyle p_{ij}}$, entao o vetor ${\displaystyle {\boldsymbol {\pi }}}$ e chamado de distribuicao estacionaria (ou medida invariante) se ${\displaystyle \forall j\in S}$ satisfaz

${\displaystyle 0\leq \pi _{j}\leq 1.}$

${\displaystyle \sum _{j\in S}\pi _{j}=1.}$

${\displaystyle \pi _{j}=\sum _{i\in S}\pi _{i}p_{ij}.}$

Uma cadeia irredutivel tem uma distribuicao estacionaria se e somente se todos os seus estados sao recorrentes positivos. ^{[ 14 ]} Nesse caso, π e unico e esta relacionada com o tempo de retorno esperado:

${\displaystyle \pi _{j}={\frac {C}{M_{j}}}\,,}$

onde ${\displaystyle C}$ e a constante de normalizacao. Alem disso, se a cadeia positiva recorrente e irredutivel e aperiodica, diz-se que tem uma distribuicao limitante; para qualquer i e j ,

${\displaystyle \lim _{n\rightarrow \infty }p_{ij}^{(n)}={\frac {C}{M_{j}}}.}$

Note-se que nao existe qualquer hipotese da distribuicao inicial; a cadeia converge para a distribuicao estacionaria independentemente de onde ele comeca. Tal ${\displaystyle \pi }$ e chamado de distribuicao em equilibrio da cadeia.

Se uma cadeia tem mais de uma classe comunicante fechada, suas distribuicoes estacionarias nao serao unicas (considere qualquer classe comunicante fechada ${\displaystyle C_{i}}$ na cadeia, cada uma tera a sua propria distribuicao estacionaria unica ${\displaystyle \pi _{i}}$. Estendendo essas distribuicoes a cadeia global, definindo todos os valores a zero fora da classe comunicante, resulta que o conjunto de medidas invariantes da cadeia original e o conjunto de todas as combinacoes convexas da { ${\displaystyle \pi _{i}}$). No entanto, se um estado j e aperiodico, entao

${\displaystyle \lim _{n\rightarrow \infty }p_{jj}^{(n)}={\frac {C}{M_{j}}}}$

e para qualquer outro estado i , sendo f _ij a probabilidade de que a cadeia visite o estado j , se ele comeca no i ,

${\displaystyle \lim _{n\rightarrow \infty }p_{ij}^{(n)}=C{\frac {f_{ij}}{M_{j}}}.}$

Se um estado i e periodico com periodo k  > 1, entao o limite

${\displaystyle \lim _{n\rightarrow \infty }p_{ii}^{(n)}}$

nao existe, embora o limite

${\displaystyle \lim _{n\rightarrow \infty }p_{ii}^{(kn+r)}}$

exista para cada inteiro r .

Analise de estado estacionario e na cadeia de Markov de tempo nao homogeneo [ editar | editar codigo-fonte ]

A cadeia de Markov nao precisa ser necessariamente o tempo homogeneo para ter uma distribuicao de equilibrio. Se ha uma distribuicao de probabilidade sobre estados ${\displaystyle {\boldsymbol {\pi }}}$ tal que

${\displaystyle \pi _{j}=\sum _{i\in S}\pi _{i}\,\Pr(X_{n+1}=j\mid X_{n}=i)}$

para cada estado j e cada tempo n , entao ${\displaystyle {\boldsymbol {\pi }}}$ e uma distribuicao em equilibrio da cadeia de Markov. Tal situacao pode ocorrer em metodos de cadeia de Markov de Monte Carlo (MCMC) em situacoes em que um numero de diferentes matrizes de transicao sao usadas, porque cada uma e eficaz para um tipo particular de mistura, mas cada matriz respeita uma distribuicao de equilibrio partilhada.

Espaco de estado finito [ editar | editar codigo-fonte ]

Se o espaco de estados e finito, a distribuicao de probabilidade de transicao pode ser representada por uma matriz, chamada de matriz de transicao, com o ( i , j )-esimo elemento de P igual

${\displaystyle p_{ij}=\Pr(X_{n+1}=j\mid X_{n}=i).\,}$

Uma vez que cada fileira de P soma um e todos os elementos sao nao-negativos, P e uma matriz estocastica direita.

Relacao distribuicao estacionaria de vetores proprios e simplices [ editar | editar codigo-fonte ]

Um π distribuicao estacionaria e um vetor (linha), cujos elementos sao nao-negativos e somam 1, mantem-se inalterado pela operacao da matriz de transicao P sobre ele e por isso e definida pela

${\displaystyle \pi \mathbf {P} =\pi .\,}$

Ao comparar essa definicao com a de um vetor proprio vemos que os dois conceitos estao relacionados e que

${\displaystyle \pi ={\frac {e}{\sum _{i}{e_{i}}}}}$

e um multiplo normalizado ( ${\displaystyle \textstyle \sum _{i}\pi _{i}=1}$) de um vetor proprio esquerdo e' da matriz de transicao P ^T com um valor proprio de 1. Se houver mais do que uma unidade de vetor proprio em seguida, a soma ponderada dos correspondentes estados estacionarios e tambem um estado estacionario. Mas para uma cadeia de Markov e geralmente mais interessados em um estado estacionario que e o limite das distribuicoes de sequencia para alguma distribuicao inicial.

Os valores de distribuicao estacionaria ${\displaystyle \textstyle \pi _{i}}$ estao associadas com o espaco de estado de P e seus vetores proprios tem as suas proporcoes relativas preservadas. Uma vez que os componentes do π sao positivos e a restricao de que a sua soma e a unidade pode ser reescrita como ${\displaystyle \textstyle \sum _{i}1\cdot \pi _{i}=1}$ vemos que o produto do ponto de π com um vetor cujos componentes sao todos 1 e unitario e que π encontra-se em um simplex.

Cadeia de Markov de tempo homogeneo com um espaco de estado finito [ editar | editar codigo-fonte ]

Se a cadeia de Markov e vez homogenea, em seguida, a matriz de transicao P e o mesmo depois de cada passo, de modo que a probabilidade de transicao do passo k pode ser calculado como a potencia k da matriz de transicao P ^k .

Se a cadeia de Markov e irredutivel e aperiodica, entao ha uma distribuicao estacionaria unica π . Alem disso, neste caso P ^k converge para uma matriz de posto um em que cada linha e o π distribuicao estacionaria, que e,

${\displaystyle \lim _{k\rightarrow \infty }\mathbf {P} ^{k}=\mathbf {1} \pi }$

onde 1 e o vetor coluna com todas as entradas iguais a 1. Isto e afirmado pelo teorema de Perron-Frobenius. Se, por qualquer meio, ${\displaystyle \scriptstyle \lim _{k\to \infty }\mathbf {P} ^{k}}$ e encontrado, entao a distribuicao estacionaria da cadeia de Markov em questao pode ser facilmente determinada para qualquer distribuicao, tal como sera explicado abaixo.

Para algumas matrizes estocasticas P , o limite ${\displaystyle \scriptstyle \lim \limits _{k\to \infty }\mathbf {P} ^{k}}$ nao existe enquanto a distribuicao e estacionaria, como mostra este exemplo:

${\displaystyle \mathbf {P} ={\begin{pmatrix}0&1\\1&0\end{pmatrix}}\qquad \mathbf {P} ^{2k}=I\qquad \mathbf {P} ^{2k+1}=\mathbf {P} }$

${\displaystyle {\begin{pmatrix}{\frac {1}{2}}&{\frac {1}{2}}\end{pmatrix}}{\begin{pmatrix}0&1\\1&0\end{pmatrix}}={\begin{pmatrix}{\frac {1}{2}}&{\frac {1}{2}}\end{pmatrix}}}$

Observe que este exemplo ilustra uma cadeia de Markov periodica.

Uma vez que existem um numero de diferentes casos especiais a considerar, o processo de encontrar este limite se existir pode ser uma tarefa longa. No entanto, existem muitas tecnicas que podem ajudar a encontrar esse limite. Seja P uma matriz n × n , e definindo ${\displaystyle \scriptstyle \mathbf {Q} =\lim _{k\to \infty }\mathbf {P} ^{k}.}$

E verdade que sempre

${\displaystyle \mathbf {QP} =\mathbf {Q} .}$

Subtraindo ' Q de ambos os lados e fatorando, tem os resultados

${\displaystyle \mathbf {Q} (\mathbf {P} -\mathbf {I} _{n})=\mathbf {0} _{n,n},}$

Onde I _n e a matriz identidade de tamanho n e 0 _n , n e a matriz zero de tamanho n × n . Multiplicando juntos matrizes estocasticos sempre produz uma outra matriz estocastica, entao Q deve ser uma matriz estocastica (ver definicao acima). Por vezes e suficiente para utilizar a equacao da matriz acima e o facto de que Q e uma matriz estocastica de resolver por Q , incluindo o facto de que a soma de cada uma das linhas em P e 1, existem n+1 equacoes para determinar n incognitas, por isso e computacionalmente mais facil se, por um lado uma seleciona uma linha em Q e substituir cada um dos seus elementos por uma, e por outro um substituir o elemento correspondente (a uma na mesma coluna) no vetor de 0, e ao lado esquerdo - multi este ultimo vetor pelo inverso da antiga matriz transformada para encontrar Q .

Aqui e um metodo para faze-lo: em primeiro lugar, definir a funcao f ( A ) para retornar a matriz A com a sua coluna mais a direita substituido com toda a 1s. Se [ f ( P ? I _n )] ^?1 existe, em seguida,

${\displaystyle \mathbf {Q} =f(\mathbf {0} _{n,n})[f(\mathbf {P} -\mathbf {I} _{n})]^{-1}.}$

A equacao matriz original e equivalente a um sistema de n × n equacoes lineares em n × n variaveis. E existem n equacoes lineares mais a partir do facto de que Q e uma matriz estocastica direito cujo cada linha somas para 1. Por isso, necessita de qualquer N × n equacoes lineares independentes das equacoes (N × N + N) para resolver os n × n variaveis. Neste exemplo, os n equacoes de "Q multiplicado pela coluna mais a direita de (P-Na)" foram substituidos por aqueles N estocasticos.

Uma coisa a notar e que, se P tem um elemento P _{i , i} na sua diagonal principal, que e igual a 1 e a linha om ou coluna i -esima e preenchida com zeros, entao essa linha ou coluna permanecera inalterada em todos os poderes subsequentes P ^k . Assim, a i -esima linha ou coluna de Q tera os 1 e os 0 de nas mesmas posicoes como em P.

Velocidade de convergencia para a distribuicao estacionaria [ editar | editar codigo-fonte ]

Como afirmado anteriormente, a partir da equacao ${\displaystyle \mathbf {\pi } =\mathbf {\pi P} }$, (se existir) o estacionaria (ou steady state ) π distribuicao e um autovetor esquerdo da linha da matriz estocastica P . Em seguida, assumindo que P e diagonalizavel ou equivalentemente que P tem n autovetores linearmente independentes, a velocidade de convergencia e elaborado da seguinte forma. (Para nao diagonalizavel, ou seja, matrizes defeituosos, pode-se comecar com a forma normal Jordan de P e prosseguir com o conjunto um pouco mais envolvidos de argumentos de uma maneira similar. ^{[ 15 ]} )

Seja U a matriz de autovetores (cada um normalizado para ter uma norma L2 igual a 1), onde cada coluna e um vetor proprio esquerdo do P e deixe Σ a matriz diagonal de valores proprios a esquerda de P , ou seja, Σ = diag( λ ₁ , λ ₂ , λ ₃ ,..., λ _n ). Entao, por eigendecomposicao

${\displaystyle \mathbf {P} =\mathbf {U\Sigma U} ^{-1}.}$

Deixe os valores proprios ser enumerados tal que 1 = | λ ₁ | > | λ ₂ | ≥ | λ ₃ | ≥ ... ≥ | λ _n |. Uma vez que P e uma matriz estocastica de linha, o seu maior valor proprio esquerda e 1. Se houver uma distribuicao estacionario original, em seguida, o valor proprio maior e o vetor proprio correspondente e tambem unico (porque nao existe nenhum outro π que resolve a equacao distribuicao estacionaria acima). Seja u _i a coluna i da matriz U , ou seja, u _i e o autovetor esquerdo de P correspondente a λ _i . Tambem sendo x ser um vetor linha comprimento n que representa uma distribuicao de probabilidade valida; ja que os autovetores u _i se distribuem por R ⁿ , podemos escrever

${\displaystyle \mathbf {x} ^{T}=\sum _{i=1}^{n}a_{i}\mathbf {u} _{i}}$

por algum conjunto de a _i ∈ ?. Se comeca-se a multiplicacao de P com x da esquerda e continuar esta operacao com os resultados, no final, obtem-se o π distribuicao estacionaria. Em outras palavras, π = u _i ← xPPP ... P = xP ^k como k vai para infinito. Que significa

${\displaystyle \mathbf {\pi } ^{(k)}=\mathbf {x} (\mathbf {U\Sigma U} ^{-1})(\mathbf {U\Sigma U} ^{-1})\cdots (\mathbf {U\Sigma U} ^{-1})}$

${\displaystyle =\mathbf {xU\Sigma } ^{k}\mathbf {U} ^{-1}}$

desde UU ^?1 = I , a matriz de identidade e de energia de uma matriz diagonal tambem e uma matriz diagonal em que cada entrada e feita para que o poder.

${\displaystyle =(a_{1}\mathbf {u} _{1}^{T}+a_{2}\mathbf {u} _{2}^{T}+\cdots +a_{n}\mathbf {u} _{n}^{T})\mathbf {U\Sigma } ^{k}\mathbf {U} ^{-1},}$

${\displaystyle =a_{1}\lambda _{1}^{k}\mathbf {u} _{1}+a_{2}\lambda _{2}^{k}\mathbf {u} _{2}+\cdots +a_{n}\lambda _{n}^{k}\mathbf {u} _{n},}$

uma vez que os vetores proprios sao ortonormais. Entao ^{[ 16 ]}

${\displaystyle =\lambda _{1}^{k}\left\{a_{1}\mathbf {u} _{1}+a_{2}\left({\frac {\lambda _{2}}{\lambda _{1}}}\right)^{k}\mathbf {u} _{2}+a_{3}\left({\frac {\lambda _{3}}{\lambda _{1}}}\right)^{k}\mathbf {u} _{3}+\cdots +a_{n}\left({\frac {\lambda _{n}}{\lambda _{1}}}\right)^{k}\mathbf {u} _{n}\right\}.}$

Desde π = u ₁ , π ^{( k )} abordagens para π como k vai para infinito com uma velocidade na ordem de λ ₂ / λ ₁ exponencialmente. Isto acontece porque | λ ₂ | ≥ | λ ₃ | ≥ ... ≥ | λ _n |, portanto, λ ₂ / λ ₁ e o termo dominante. Um ruido aleatorio na distribuicao de estado π tambem pode acelerar essa convergencia com a distribuicao estacionaria. ^{[ 17 ]}

Cadeia de Markov reversiveis [ editar | editar codigo-fonte ]

Uma cadeia de Markov e dita ser reversivel se existe uma distribuicao de probabilidade π sobre os seus estados tais que

${\displaystyle \pi _{i}\Pr(X_{n+1}=j\mid X_{n}=i)=\pi _{j}\Pr(X_{n+1}=i\mid X_{n}=j)}$

para todos os tempos n e todos os estados i e j . Esta condicao e conhecida como condicao de balanco detalhado (alguns livros chamam a equacao de balanco local).

Considerando-se um tempo arbitrario n fixo e usando a abreviacao

${\displaystyle p_{ij}=\Pr(X_{n+1}=j\mid X_{n}=i)\,,}$

a equacao do balanco detalhado pode ser escrita de forma mais compacta como

${\displaystyle \pi _{i}p_{ij}=\pi _{j}p_{ji}\,.}$

O tempo de um so passo a partir de n a n +1 pode ser pensado como tendo cada pessoa i que inicialmente π _i dolares e pagar cada pessoa j uma fracao p _ij dela. A condicao de balanco detalhado afirma que a cada pagamento, a outra pessoa paga exatamente a mesma quantidade de dinheiro de volta. ^{[ 18 ]} E evidente que a quantidade total de dinheiro π que cada pessoa tem permanece o mesmo apos o passo de tempo, uma vez que cada dolar gasto e equilibrado por um dolar correspondente recebida. Isto pode ser demonstrado mais formalmente pela igualdade

${\displaystyle \sum _{i}\pi _{i}p_{ij}=\sum _{i}\pi _{j}p_{ji}=\pi _{j}\sum _{i}p_{ji}=\pi _{j}\,,}$

que afirma essencialmente que a quantidade total de dinheiro pessoa j recebe (incluindo de si mesmo) durante o passo de tempo e igual a quantidade de dinheiro que ele paga a outros, o que equivale a todo o dinheiro que tinha inicialmente porque foi assumido que todo o dinheiro e gasto (isto e p _ji soma 1 sobre i ). A suposicao e uma questao tecnica, porque o dinheiro nao e realmente usada e simplesmente pensado como sendo pagos de pessoa j para si mesmo (isto e p _jj nao e necessariamente zero).

Como n foi arbitrario, este raciocinio e valido para qualquer n , e, portanto, para cadeias de Markov reversiveis π e sempre uma distribuicao no estado estacionario de Pr( X _n+1  =  j  |  X _n  =  i ) para cada n .

Se a cadeia de Markov comeca na distribuicao em estado estacionario, isto e, se Pr( X ₀  =  i ) = π _i , entao Pr( X _n  =  i ) = π _i para todo o n e a equacao de equilibrio detalhada pode ser escrito como

${\displaystyle \Pr(X_{n}=i,X_{n+1}=j)=\Pr(X_{n+1}=i,X_{n}=j)\,.}$

Os lados esquerdo e direito desta ultima equacao sao identicas, exceto para uma reversao dos indices de tempo n e n  + 1. criterio de Kolmogorov da uma condicao necessaria e suficiente para uma cadeia de Markov para ser reversivel directamente a partir das probabilidades de transicao de matriz. O criterio exige que os produtos de probabilidades em torno de cada circuito fechado sao os mesmos em ambas as direccoes em torno do circuito.

Cadeias de Markov reversiveis sao comuns na cadeia de Markov Monte Carlo (MCMC) se aproxima, porque a equacao do balanco detalhado para a distribuicao π desejada implica necessariamente que a cadeia de Markov foi construido de modo que π e uma distribuicao em estado estacionario. Mesmo com correntes de Markov de tempo nao homogenea, em que multiplas matrizes de transicao sao usados, se cada matriz de transicao exibe equilibrio detalhada com a distribuicao π desejada, isto implica necessariamente que π e uma distribuicao em estado estacionario da cadeia de Markov.

Cadeia de Markov reversivel mais proxima [ editar | editar codigo-fonte ]

Para qualquer cadeia de Markov de tempo homogeneo dada por uma matriz de transicao ${\displaystyle P\in \mathbb {R} ^{n\times n}}$, qualquer norma ${\displaystyle ||\cdot ||}$ em ${\displaystyle \mathbb {R} ^{n\times n}}$ que e induzido por um produto escalar, e qualquer vetor probabilidade ${\displaystyle \pi }$, existe uma matriz de transicao unica ${\displaystyle P^{*}}$ que e reversivel de acordo com a ${\displaystyle \pi }$ e que esta mais proxima de ${\displaystyle P}$ de acordo com a norma ${\displaystyle ||\cdot ||}$. A matriz ${\displaystyle P^{*}}$ pode ser calculada resolvendo um problema de otimizacao quadratico-convexa. ^{[ 19 ]}

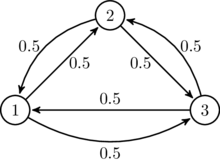
Por exemplo, considere a seguinte cadeia de Markov:

Esta cadeia de Markov nao e reversivel. De acordo com o Frobenius Norm a cadeia de Markov reversiveis mais proximo de acordo com ${\displaystyle \pi =\left({\frac {1}{3}},{\frac {1}{3}},{\frac {1}{3}}\right)}$ pode ser calculado como

Se escolher o vetor de probabilidade aleatoriamente como ${\displaystyle \pi =\left({\frac {1}{4}},{\frac {1}{4}},{\frac {1}{2}}\right)}$, entao a cadeia de Markov reversivel mais proxima de acordo com a norma de Frobenius e dada aproximadamente pela

Esquema de Bernoulli [ editar | editar codigo-fonte ]

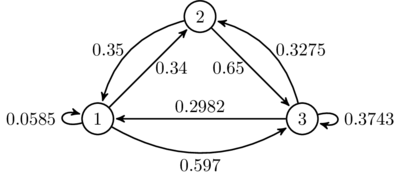
Um esquema de Bernoulli e um caso especial de uma cadeia de Markov, onde a matriz de probabilidades de transicao tem linhas identicas, o que significa que o proximo estado e ainda independente do estado corrente (para alem de serem independentes dos estados anteriores). Um esquema de Bernoulli com apenas dois estados possiveis e conhecido como um processo de Bernoulli.

Espaco geral do estado [ editar | editar codigo-fonte ]

Para uma visao geral de cadeias de Markov em um espaco geral do estado, ver as cadeias de Markov artigo em um espaco de estado mensuravel.

Cadeias Harris [ editar | editar codigo-fonte ]

Muitos resultados para cadeias de Markov com espaco de estados finitos podem ser generalizados para cadeias com espaco de estado incontavel atraves de cadeias de Harris. A ideia principal e para ver se ha um ponto no espaco de estado que os hits da cadeia com probabilidade um. Geralmente, nao e verdadeiro para o espaco de estado continuo, no entanto, podemos definir conjuntos A e B , juntamente com um numero positivo ε e uma medida de probabilidade ρ , de tal modo que

1. ${\displaystyle {\text{Se }}\tau _{A}=\inf\{n\geq 0:X_{n}\in A\},{\text{ entao }}P_{z}(\tau _{A}<\infty )>0{\text{ para todo }}z.}$

1. ${\displaystyle {\text{Se }}x\in A{\text{ e }}C\subset B,{\text{ entao }}p(x,C)\geq \varepsilon \rho (C).}$

Em seguida, pode entrar em colapso os conjuntos em um ponto auxiliar α , e uma cadeia Harris recorrente pode ser modificado para conter α . Finalmente, o conjunto de cadeias Harris e um nivel confortavel de generalidade, a qual e ampla o suficiente para conter um grande numero de exemplos interessantes, ainda restritiva suficiente para permitir uma teoria rica.

O uso de cadeias de Markov em cadeia de Markov metodos de Monte Carlo abrange casos em que o processo segue um espaco de estado continuo.

Cadeias de Markov interagindo localmente [ editar | editar codigo-fonte ]

Considerando-se uma colecao de cadeias de Markov cuja evolucao leva em conta o estado de outras cadeias de Markov, esta relacionada com a nocao de interagir localmente cadeias de Markov. Isso corresponde a situacao em que o espaco de estado tem uma forma de produto. Veja interagindo sistema de particulas e automatos celulares estocastico (probabilistica automatos celulares). Ver, por exemplo Interacao de Markov processos. ^{[ 20 ]} ou ^{[ 21 ]}

Aplicacoes [ editar | editar codigo-fonte ]

A pesquisa tem relatado a aplicacao e utilidade das cadeias de Markov em uma ampla gama de topicos, tais como a fisica, quimica, medicina, musica, teoria dos jogos e esportes.

Fisica [ editar | editar codigo-fonte ]

Sistemas Markovianos aparecem extensivamente em termodinamica e mecanica estatistica, sempre que as probabilidades sao usados para representar detalhes desconhecidos ou nao modelados do sistema, se pode presumir-se que a dinamica e invariante no tempo, e que nenhuma historia relevante precisa ser considerado que nao estiver incluido na descricao do estado.

Quimica [ editar | editar codigo-fonte ]

Cadeias de Markov e processos de Markov de tempo continuo sao uteis em quimica quando os sistemas fisicos aproximam a propriedade de Markov. O modelo classico da actividade da enzima, a cinetica de Michaelis-Menten, pode ser visto como uma cadeia de Markov, onde em cada etapa de tempo a reaccao prossegue em algum sentido. Enquanto Michaelis-Menten e bastante simples, redes de reaccao muito mais complicados tambem podem ser modeladas com cadeias de Markov.

Um algoritmo baseado numa cadeia de Markov tambem foi utilizado para focar o crescimento baseado no fragmento de produtos quimicos in silico no sentido de uma classe desejada de compostos, tais como farmacos ou produtos naturais. ^{[ 22 ]} Como uma molecula e cultivada, um fragmento e seleccionado a partir da molecula nascente como o estado "corrente". Nao e do conhecimento do seu passado (isto e, nao esta consciente de que ja se encontra ligado a ele). E, em seguida, passa para o proximo estado, quando um fragmento e ligado a ele. As probabilidades de transicao sao treinados em bases de dados das classes autenticas de compostos.

Alem disso, o crescimento (e composicao) dos copolimeros pode ser modelada utilizando cadeias de Markov. Com base nas relacoes de reactividade dos monomeros que formam a cadeia polimerica em crescimento, a composicao da corrente pode ser calculada (por exemplo, se monomeros tendem a adicionar de forma alternada ou em funcionamentos longos do mesmo monomero). Devido aos efeitos estericos, de segunda ordem efeitos de Markov pode tambem desempenhar um papel no crescimento de algumas cadeias de polimero.

Do mesmo modo, tem sido sugerido que a cristalizacao e o crescimento de alguns dos materiais de oxido de superrede epitaxiais pode ser descrito com precisao por Cadeias de Markov. ^{[ 23 ]}

Ensaio [ editar | editar codigo-fonte ]

Muitos teoricos tem proposto a ideia do teste estatistico cadeia de Markov (MCST), um metodo de conjuncao cadeias de Markov para formar um "Markov cobertor", organizando essas cadeias em varias camadas recursiva ( "wafering") e producao de testes mais eficientes conjuntos-amostras -como um substituto para testes exaustivos. MCSTs tambem tem usos em redes baseadas no estado temporais; O artigo de Chilukuri et al. intitulado "temporais Networks Incerteza raciocinio para Evidence fusao com Aplicacoes para objeto de Deteccao e Acompanhamento" (ScienceDirect) da um estudo de fundo e caso para aplicar MCSTs a uma ampla gama de aplicacoes.

Reconhecimento de fala [ editar | editar codigo-fonte ]

Modelos ocultos de Markov sao a base para a maioria dos sistemas de reconhecimento de voz automaticas modernas. ^{[ 24 ]}

Ciencias da informacao [ editar | editar codigo-fonte ]

Cadeias de Markov sao usados em todo o processamento da informacao. famosa 1948 de papel uma teoria matematica de Claude Shannon de comunicacao, que em uma unica etapa criou o campo da teoria da informacao, abre com a introducao do conceito de entropia atraves de modelagem Markov do idioma Ingles. Tais modelos idealizados pode capturar muitas das regularidades estatisticas de sistemas. Mesmo sem descrever a estrutura completa do sistema perfeitamente, tais modelos de sinal podem tornar possivel a compressao de dados muito eficaz atraves de tecnicas de codificacao de entropia, como codificacao aritmetica. Eles tambem permitem que estimacao de estado eficaz e reconhecimento de padroes. Cadeias de Markov tambem desempenham um papel importante no aprendizado por reforco.

Cadeias de Markov sao tambem a base para modelos ocultos de Markov, que sao um instrumento importante para diversas areas como redes telefonicas (que utilizam o algoritmo Viterbi para correcao de erro), reconhecimento de voz e bioinformatica (como na deteccao de rearranjos ^{[ 25 ]} ).

O algoritmo de compressao de dados sem perdas LZMA combina cadeias de Markov com compressao Lempel-Ziv para alcancar taxas de compressao muito elevados.

Teoria de filas [ editar | editar codigo-fonte ]

Cadeias de Markov sao a base para o tratamento analitico das filas (teoria de filas). Agner Krarup Erlang iniciou o assunto em 1917. ^{[ 26 ]} Isso os torna critico para otimizar o desempenho de redes de telecomunicacoes, em que as mensagens muitas vezes competem por recursos limitados (como a largura de banda). ^{[ 27 ]}

Aplicacoes de Internet [ editar | editar codigo-fonte ]

O PageRank de uma pagina da web como usado pelo Google e definida por uma cadeia de Markov. ^{[ 28 ]} E a probabilidade de estar em pagina ${\displaystyle i}$ displaystyle na distribuicao estacionaria sobre a seguinte cadeia de Markov em todas as paginas Web (conhecidas). Se ${\displaystyle N}$ e o numero de paginas da Web conhecidas, e uma pagina ${\displaystyle i}$ tem ${\displaystyle k_{i}}$ links para ela, entao ele tem probabilidade de transicao ${\displaystyle {\frac {\alpha }{k_{i}}}+{\frac {1-\alpha }{N}}}$ para todas as paginas que estao ligadas a ela e ${\displaystyle {\frac {1-\alpha }{N}}}$ para todas as paginas que estao nao ligadas. O parametro ${\displaystyle \alpha }$ e considerado como sendo cerca de 0,85.

Os modelos de Markov tambem tem sido utilizados para analisar o comportamento de navegacao Web de utilizadores. web link transicao de um usuario em um determinado site pode ser modelado usando modelos de Markov de ordem segunda primeira ou e pode ser usado para fazer previsoes sobre a navegacao futuro e para personalizar a pagina da web para um usuario individual.

Estatistica [ editar | editar codigo-fonte ]

Metodos da cadeia de Markov tambem se tornaram muito importantes para a geracao de sequencias de numeros aleatorios para refletir com precisao as distribuicoes de probabilidade desejados muito complicadas, atraves de um processo chamado de Markov chain Monte Carlo (MCMC) . Nos ultimos anos, este tem revolucionado a praticabilidade de metodos de inferencia bayesiana, permitindo uma ampla gama de distribuicoes posteriores a ser simulada e seus parametros encontrados numericamente.

Economia e financas [ editar | editar codigo-fonte ]

Cadeias de Markov sao utilizados em financas e economia para modelar uma variedade de diferentes fenomenos, incluindo os precos dos ativos e falhas de mercado. O primeiro modelo financeiro para usar uma cadeia de Markov foi de Prasad et al. em 1974. ^{[ 29 ]} Outro foi o modelo de mudanca de regime de James D. Hamilton (1989), em que uma cadeia de Markov e usado para modelar alterna entre periodos de crescimento alta e baixa do PIB (ou, alternativamente, expansoes economicas e recessoes). ^{[ 30 ]} Um exemplo mais recente e o modelo Multifractal Switching Markov de Laurent E. Calvet e Adlai J. Fisher, que foi construido sobre a conveniencia de modelos anteriores de mudanca de regime. ^{[ 31 ] [ 32 ]} Ele usa um arbitrariamente grande cadeia de Markov para dirigir o nivel de volatilidade dos retornos de ativos.

Macroeconomia dinamica usa fortemente cadeias de Markov. Um exemplo esta usando cadeias de Markov de precos modelo exogenamente de equidade (estoque) em um ambiente de equilibrio geral. ^{[ 33 ]}

As agencias de notacao produzir tabelas anuais das probabilidades de transicao para as obrigacoes de diferentes classificacoes de credito. ^{[ 34 ]}

Ciencias Sociais [ editar | editar codigo-fonte ]

Cadeias de Markov sao geralmente usados para descrever argumentos dependentes do caminho, onde as configuracoes estruturais atuais condicionam os resultados futuros. Um exemplo e a reformulacao da ideia, originalmente devido a de Karl Marx Das Kapital, amarrando o desenvolvimento economico com a ascensao do capitalismo. Na pesquisa atual, e comum o uso de uma cadeia de Markov para modelar como quando um pais atinge um determinado nivel de desenvolvimento economico, a configuracao de fatores estruturais, tais como tamanho da burguesia comercial, a proporcao da populacao urbana a residencia rural, a taxa de de mobilizacao politica, etc., ira gerar uma maior probabilidade de transicao de autoritario para o regime democratico. ^{[ 35 ]}

Biologia matematica [ editar | editar codigo-fonte ]

Cadeias de Markov tambem tem muitas aplicacoes na modelagem biologica, em particular os processos de populacoes, que sao uteis em processos de modelagem que sao (pelo menos) analogo ao populacoes biologicas. A matriz de Leslie e um exemplo deste tipo, embora algumas das suas entradas nao sao probabilidades (que pode ser maior do que 1). Outro exemplo e a modelacao das celulas em forma dividindo folhas de celulas epiteliais. ^{[ 36 ]} Ainda um outro exemplo e o estado dos canais de ions em membranas celulares.

Cadeias de Markov tambem sao utilizados em simulacoes da funcao cerebral, tais como a simulacao do neocortex de mamifero. ^{[ 37 ]}

Genetica [ editar | editar codigo-fonte ]

Cadeias de Markov tem sido usados em genetica de populacoes, a fim de descrever a mudanca nas frequencias de genes em pequenas populacoes afetadas por deriva genetica, por exemplo, na forma de equacao de difusao descrita por Motoo Kimura. ^{[ 38 ]}

Jogos [ editar | editar codigo-fonte ]

Cadeias de Markov pode ser usado para modelar muitos jogos de azar. Jogos infantis Snakes and Ladders e "Hi Ho! Cherry-O", por exemplo, sao representados exatamente por cadeias de Markov. Em cada turno, o jogador comeca em um determinado estado (em um determinado quadrado) e de la tem chances de se mudar para alguns outros estados (quadrados) fixo.

Musica [ editar | editar codigo-fonte ]

Cadeias de Markov sao empregados na composicao de musica algoritmica, particularmente em softwares como o CSound, Max e SuperCollider. Em uma cadeia de primeira ordem, os estados do sistema tornam-se notas ou valores de altura, e um vetor de probabilidade para cada nota e construido, completando uma matriz de probabilidade de transicao (ver abaixo). Um algoritmo e construido para produzir valores de altura de saida com base nos coeficientes de matriz de transicao, que pode ser de alturas MIDI, de frequencias (Hz), ou qualquer outra metrica desejavel. ^{[ 39 ]} matriz de 1ª ordem

Matriz de primeira ordem

Nota	A	C ♯	E ♭
A	0.1	0.6	0.3
C ♯	0.25	0.05	0.7
E ♭	0.7	0.3	0

Matriz de segunda ordem

Notas	A	D	G
AA	0.18	0.6	0.22
AD	0.5	0.5	0
AG	0.15	0.75	0.1
DD	0	0	1
DA	0.25	0	0.75
DG	0.9	0.1	0
GG	0.4	0.4	0.2
GA	0.5	0.25	0.25
GD	1	0	0

Uma cadeia de Markov de segunda ordem pode ser introduzida ao considerar o estado atual e tambem o estado anterior, conforme indicado na segunda tabela. Cadeias de ordem "n" tendem a "agrupar" notas particulares juntas, enquanto 'quebrando' para outros padroes e sequencias ocasionalmente. Estas cadeias de ordem superior tendem a gerar resultados com um sentido de estrutura frasal, ao inves do 'vaguear' produzido por um sistema de primeira ordem. ^{[ 40 ]}

Cadeias de Markov podem ser usadas estruturalmente, como na Analogique A e B de Xenakis. ^{[ 41 ]} Cadeias de Markov tambem sao utilizadas em sistemas que utilizam um modelo de Markov para reagir interativamente a entrada de musica. ^{[ 42 ]}

Normalmente sistemas musicais precisa impor restricoes de controle especificas sobre as sequencias de comprimento finito que geram, mas as restricoes de controle nao sao compativeis com os modelos de Markov, uma vez que induzem dependencias de longo alcance que violam a hipotese de Markov de memoria limitada. De modo a ultrapassar esta limitacao, uma nova abordagem tem sido proposta. ^{[ 43 ]}

Beisebol [ editar | editar codigo-fonte ]

Modelos de cadeia de Markov foram usados na analise de beisebol avancado desde 1960, embora a sua utilizacao e ainda raro. Cada meio-turno de um jogo de beisebol se encaixa o estado da cadeia de Markov, quando o numero de corredores e saidas sao considerados. Durante qualquer no bastao, existem 24 possiveis combinacoes de numero de saidas e a posicao dos corredores. Mark Pankin mostra que modelos de cadeia de Markov pode ser usado para avaliar corridas criadas para ambos os jogadores individuais, bem como uma equipe. ^{[ 44 ]} Ele tambem discute varios tipos de estrategias e condicoes de jogo: como os modelos da cadeia de Markov tem sido usados para analisar estatisticas para situacoes de jogo, tais como Bunting e base de roubo e diferencas quando se joga na grama ou na relva sintetica. ^{[ 45 ]}

Geradores de texto de Markov [ editar | editar codigo-fonte ]

Processos de Markov tambem pode ser usado para gerar texto superficialmente com aparencia real dado um documento de exemplo: eles sao usados em uma variedade de software de recreio "gerador de parodia" (ver comunicado de imprensa dissociada, Jeff Harrison, ^{[ 46 ]} Mark V Shaney ^{[ 47 ] [ 48 ]} ). Esses processos tambem sao usados por spammers para injetar paragrafos ocultos aparencia reais em e-mail nao solicitado e postar comentarios em uma tentativa de obter essas mensagens passado filtros de spam.

No campo da bioinformatica, eles podem ser utilizados para simular as sequencias de DNA. ^{[ 49 ]}

Ajustando [ editar | editar codigo-fonte ]

Ao ajustar uma cadeia de Markov aos dados, situacoes nas quais os parametros descrevem mal a situacao podem destacar tendencias interessantes. ^{[ 50 ] [ 51 ] [ 52 ]}

Historia [ editar | editar codigo-fonte ]

Andrey Markov produziu os primeiros resultados (1906) para estes processos, puramente teorica. ^{[ 53 ]} A generalizacao para espacos de estado infinitos contaveis foi dada por Kolmogorov (1936). Cadeias de Markov estao relacionados com o movimento Browniano e a hipotese ergodica, dois topicos da fisica que eram importante nos primeiros anos do seculo XX. No entanto, Markov primeiro usou as cadeias em 1906 como parte de seu argumento contra Pavel Nekrasov, em particular para fazer o caso que a lei dos grandes numeros pode ser estendido para eventos dependentes. ^{[ 54 ]} Em 1913, ele aplicou suas descobertas para os primeiros 20.000 cartas de Eugene Onegin de Pushkin. ^{[ 54 ]} Em 1917, a aplicacao mais pratica de seu trabalho foi feito por Erlang obter formulas para a perda de chamadas e tempo de espera nas redes telefonicas. ^{[ 26 ]}

Seneta fornece uma conta de motivacoes de Markov e desenvolvimento inicial da teoria. ^{[ 55 ]} O termo "cadeia" foi utilizado pela Markov (1906) sugerem que uma sequencia de variaveis dependentes emparelhadas. ^{[ 56 ]}

Referencias

Ligacoes externas [ editar | editar codigo-fonte ]

• ≪Um gerador de Letras de Musica Markoviano≫ . que utiliza letras ja existentes para criar aleatoriamente outras. Pode-se utilizar cadeias de varias ordens. O codigo-fonte em PHP esta disponivel.  
• ≪Um compressor de textos≫ . baseado em cadeias de Markov feito em JavaScript, como trabalho de uma disciplina sobre processos estocasticos da Universidade de Sao Paulo (USP).  
• ≪Aplicacao na Dinamica da Metastase do Cancer de Mama e Pulmao≫  
• ≪Processos Estocasticos: Curso com aplicacoes em Machine Learning, Robotica e Data Science - Aulas online do IPRJ/UERJ, com enfase em cadeias de Markov≫ . (em portugues)  

• Portal de probabilidade e estatistica