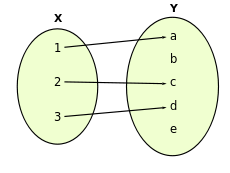
 Uma funcao nao injetiva e nao sobrejetiva do dominio X para o contradominio Y. A funcao e nao injetova pois ha dois elementos do dominio ligados a um mesmo elemento do contradominio (cor vermelha). A funcao e nao sobrejetiva pois ha elementos de Y sem correspondentes em X (cores azul e lilas).
Uma funcao nao injetiva e nao sobrejetiva do dominio X para o contradominio Y. A funcao e nao injetova pois ha dois elementos do dominio ligados a um mesmo elemento do contradominio (cor vermelha). A funcao e nao sobrejetiva pois ha elementos de Y sem correspondentes em X (cores azul e lilas).
Uma
funcao
e uma
relacao
de um
conjunto
 com um conjunto
com um conjunto
 . Denotamos uma funcao por
. Denotamos uma funcao por

 onde
onde
 e o nome da funcao,
e o nome da funcao,
 e chamado de
dominio
,
e chamado de
dominio
,
 e chamado de
contradominio
e
e chamado de
contradominio
e
 expressa a lei de formacao (relacao) dos elementos,
expressa a lei de formacao (relacao) dos elementos,
 com os elementos
com os elementos
 Considerando o conjunto de pares ordenados
Considerando o conjunto de pares ordenados
 de
de
 x
x
 , teremos uma relacao entre os elementos de
, teremos uma relacao entre os elementos de
 e de
e de
 ou, simplesmente,
relacao binaria
de
ou, simplesmente,
relacao binaria
de
 em
em
 .
[
1
]
Para cada elemento do dominio, existira um unico correspondente no contradominio, esse correspondente e conhecido como
imagem
. De acordo com suas caracteristicas, as funcoes sao agrupadas em varias categorias, entre as principais temos:
funcao trigonometrica
,
funcao afim (ou funcao polinomial do 1° grau)
,
funcao modular
,
funcao quadratica
(ou funcao polinomial do 2° grau),
funcao exponencial
,
funcao logaritmica
,
funcao polinomial
, dentre inumeras outras.
[
2
]
[
3
]
[
1
]
.
[
1
]
Para cada elemento do dominio, existira um unico correspondente no contradominio, esse correspondente e conhecido como
imagem
. De acordo com suas caracteristicas, as funcoes sao agrupadas em varias categorias, entre as principais temos:
funcao trigonometrica
,
funcao afim (ou funcao polinomial do 1° grau)
,
funcao modular
,
funcao quadratica
(ou funcao polinomial do 2° grau),
funcao exponencial
,
funcao logaritmica
,
funcao polinomial
, dentre inumeras outras.
[
2
]
[
3
]
[
1
]
As funcoes sao definidas por relacionar constantes e variaveis para descrever fenomenos naturais e tecnologicos, estudadas em diversas areas do conhecimento.
[
4
]
Deve-se notar que as palavras "funcao", "mapeamento", "mapa" e "transformacao" sao geralmente usadas como termos equivalentes. Muitas leis cientificas e muitos principios de Engenharia descrevem funcao como uma quantidade dependendo de outra. Em 1673, essa ideia foi formaliza por Leibniz, quando cunhou o termo para indicar a dependencia de uma quantidade em relacao a uma outra.
[
5
]
Alem disso pode-se ocasionalmente se referir a funcoes como "funcoes bem definidas" ou "funcoes totais". O conceito de uma
funcao
e uma generalizacao da nocao comum de
formula matematica
. As funcoes descrevem
relacoes matematicas
especiais entre dois elementos. Intuitivamente, uma funcao e uma maneira de associar a cada valor do argumento
 (as vezes denominado
variavel independente
) a um
unico
valor da funcao
(as vezes denominado
variavel independente
) a um
unico
valor da funcao
 (tambem conhecido como
variavel dependente
). Isto pode ser feito atraves de uma
equacao
, um relacionamento
grafico
, diagramas representando os dois conjuntos, uma regra de associacao, uma tabela de correspondencia, etc... Muitas vezes, e util associar cada par de elementos relacionados pela funcao com um ponto em um espaco adequado (por exemplo, no
espaco
(tambem conhecido como
variavel dependente
). Isto pode ser feito atraves de uma
equacao
, um relacionamento
grafico
, diagramas representando os dois conjuntos, uma regra de associacao, uma tabela de correspondencia, etc... Muitas vezes, e util associar cada par de elementos relacionados pela funcao com um ponto em um espaco adequado (por exemplo, no
espaco
 geometricamente representado no
plano cartesiano
). Neste caso, a exigencia de unicidade da imagem (valor da funcao) implica um unico ponto para cada entrada
geometricamente representado no
plano cartesiano
). Neste caso, a exigencia de unicidade da imagem (valor da funcao) implica um unico ponto para cada entrada
 (valor do argumento).
[
1
]
[
6
]
[
7
]
(valor do argumento).
[
1
]
[
6
]
[
7
]
Assim como a nocao intuitiva de funcoes nao se limita a calculos usando numeros individuais, a nocao matematica de funcoes nao se limita a calculos e nem mesmo a situacoes que envolvam numeros. De forma geral, uma funcao liga um
dominio
(conjunto de valores de entrada) com um segundo conjunto, o
contradominio
(conjunto de valores de saida), de tal forma que a cada elemento do dominio esta associado exatamente um elemento do contradominio. O conjunto dos elementos
 do contradominio para os quais existe pelo menos um
do contradominio para os quais existe pelo menos um
 no dominio tal que
no dominio tal que
 (i.e.,
(i.e.,
 se relaciona com
se relaciona com
 ), e o
conjunto imagem
ou chamado simplesmente de imagem da funcao.
[
7
]
), e o
conjunto imagem
ou chamado simplesmente de imagem da funcao.
[
7
]
- Se uma variavel
 depende de uma variavel
depende de uma variavel
 de tal modo que cada valor de
de tal modo que cada valor de
 determina exatamente um valor de
determina exatamente um valor de
 , entao dizemos que
, entao dizemos que
 e uma funcao de
e uma funcao de
 [
5
]
[
5
]
- Uma funcao
 e uma regra que associa uma unica saida a cada entrada. Se a entrada for denotada por
e uma regra que associa uma unica saida a cada entrada. Se a entrada for denotada por
 , entao a saida e denotada por
, entao a saida e denotada por
 .
[
5
]
.
[
5
]
- Sejam dados os conjuntos

 uma relacao
uma relacao
 e o conjunto dos pares ordenados
e o conjunto dos pares ordenados
 Dizemos que
Dizemos que
 e uma funcao se, e somente se, para todos
e uma funcao se, e somente se, para todos
 com
com
 temos
temos
 Ou, em outras palavras, para todo
Ou, em outras palavras, para todo
 existe no maximo um
existe no maximo um
 tal que
tal que
 se relaciona com
se relaciona com
 [
1
]
Assim sendo, escrevemos
[
1
]
Assim sendo, escrevemos
 quando
quando
 se relaciona com
se relaciona com
 por
por
 O conjunto
O conjunto
 e chamado de conjunto de partida e
e chamado de conjunto de partida e
 e chamado de contradominio da funcao
e chamado de contradominio da funcao
 Outra maneira de dizer isto e afirmar que
Outra maneira de dizer isto e afirmar que
 e uma
relacao binaria
entre os dois conjuntos tal que
e uma
relacao binaria
entre os dois conjuntos tal que
 e
univoca,
i.e. se
e
univoca,
i.e. se
 e
e
 entao
entao
 Algumas vezes, na definicao de funcao, impoe-se que todo o elemento do conjunto
Algumas vezes, na definicao de funcao, impoe-se que todo o elemento do conjunto
 se relaciona com algum elemento de
se relaciona com algum elemento de

Vejamos as seguintes relacoes


|
Esta
nao
e uma funcao, pois o elemento
 e associado (se relaciona) com dois elementos e associado (se relaciona) com dois elementos
 a saber com a saber com
 Esta e, entretanto, um exemplo das chamadas
funcoes multivaloradas
. Esta e, entretanto, um exemplo das chamadas
funcoes multivaloradas
.
|

|
Este e um exemplo de uma funcao dita parcial (
funcao parcial
), pois ha pelo menos um elemento no conjunto de partida, a saber
 que nao se relaciona com nenhum elemento do contradominio (conjunto que nao se relaciona com nenhum elemento do contradominio (conjunto
 ). ).
|
|
Este e um exemplo de uma funcao dita discreta (veja,
funcao discreta
). Sua lei de correspondencia pode ser escrita da seguinte forma:
 |
Podemos usar uma funcao para modelar o numero de individuos em uma populacao de acordo com o tempo (
modelos de crescimento demografico
). Por exemplo, denotando o tempo por
 e o numero de individuos em um dado tempo
e o numero de individuos em um dado tempo
 por
por
 escrevemos
escrevemos

 Assim, temos abstratamente modelado o numero de individuos (variavel dependente) em funcao do tempo (
variavel independente
). Aqui, o nome da funcao foi arbitrariamente escolhido como
Assim, temos abstratamente modelado o numero de individuos (variavel dependente) em funcao do tempo (
variavel independente
). Aqui, o nome da funcao foi arbitrariamente escolhido como
 o conjunto de partida e o conjunto dos
numeros reais
nao negativos (assumindo que o tempo e continuo e nao negativo) e o contradominio e o conjunto dos
numeros naturais
(assumindo que o numero de individuos e sempre um
numero inteiro
nao negativo).
o conjunto de partida e o conjunto dos
numeros reais
nao negativos (assumindo que o tempo e continuo e nao negativo) e o contradominio e o conjunto dos
numeros naturais
(assumindo que o numero de individuos e sempre um
numero inteiro
nao negativo).
Da definicao, temos que uma funcao tem um nome, um conjunto de partida, um contradominio (conjunto de chegada) e uma lei de correspondencia. Por exemplo, denotamos

 onde
onde
 e o nome da funcao,
e o nome da funcao,
 e seu conjunto de partida,
e seu conjunto de partida,
 e seu contradominio e
e seu contradominio e
 denota sua lei de correspondencia.
denota sua lei de correspondencia.
Em muitos casos, nem todos os elementos do conjunto de partida se relacionam com algum elemento do contradominio. Aqueles que se relacionam sao elementos do chamado
dominio da funcao
. Mais precisamente, o dominio de uma funcao

 e o conjunto:
e o conjunto:

Tambem, geralmente, nem todos os elementos do contradominio se relacionam com algum elemento do conjunto de partida. Aqueles que se relacionam sao elementos da chamada
imagem da funcao
. A imagem de uma funcao


e o conjunto:

Seja

 onde o conjunto de partida e dada por
onde o conjunto de partida e dada por
 e o contradominio por
e o contradominio por
 Pela lei de correspondencia, vemos que, neste caso,
Pela lei de correspondencia, vemos que, neste caso,
 e
e
 Veja a ilustracao.
Veja a ilustracao.
 Representacao em
diagrama de Venn
da funcao
Representacao em
diagrama de Venn
da funcao

 A imagem de
A imagem de
 esta delineada por uma linha tracejada.
esta delineada por uma linha tracejada.
 Esboco do grafico de uma funcao arbitraria de uma variavel com representacao do par ordenado
Esboco do grafico de uma funcao arbitraria de uma variavel com representacao do par ordenado

O grafico de uma funcao

 e o conjunto:
e o conjunto:

e o conjunto dos
pares ordenados

tal que

Quando possivel, usualmente fazemos uma representacao geometrica do grafico da funcao. Tal representacao e usualmente chamada de esboco do grafico da funcao (ou, simplesmente grafico, quando subentendido).
Popularmente, temos os graficos de funcoes de uma variavel, para as quais seu esboco e dado pelo conjunto de pontos
 no plano cartesiano (veja a ilustracao). Neste caso, usualmente as variaveis independentes sao chamadas de
abcissas
e marcadas sobre o eixo horizontal (chamado de eixo das abcissas). As variaveis dependentes sao chamadas de
ordenadas
e marcadas sobre o eixo vertical (chamado de eixo das ordenadas).
no plano cartesiano (veja a ilustracao). Neste caso, usualmente as variaveis independentes sao chamadas de
abcissas
e marcadas sobre o eixo horizontal (chamado de eixo das abcissas). As variaveis dependentes sao chamadas de
ordenadas
e marcadas sobre o eixo vertical (chamado de eixo das ordenadas).
Funcoes sao usualmente classificadas quanto a sua imagem como:
funcoes injetoras
,
funcoes sobrejetoras
e
funcoes bijetoras
.
Seja dada a funcao

 Por definicao,
Por definicao,
 e injetora (ou injetiva) se, e somente se, para todos
e injetora (ou injetiva) se, e somente se, para todos
 temos
temos
 A funcao
A funcao
 e dita sobrejetora (ou sobrejetiva) quando
e dita sobrejetora (ou sobrejetiva) quando
 Por fim, uma funcao injetora e sobrejetora e dita ser bijetora (ou bijetiva). Veja a seguinte tabela.
Por fim, uma funcao injetora e sobrejetora e dita ser bijetora (ou bijetiva). Veja a seguinte tabela.
| Tipo de funcao
|
Caracteristica da funcao
|
Conjunto imagem
|
Explicacao visual
|
Exemplo
|
Admite
funcao inversa
? E inversivel?
|
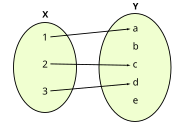
| Injetora ou injetiva
|
Cada elemento da imagem esta associado a apenas um elemento do dominio, isto e, quando
 ≠ ≠
 no dominio tem-se no dominio tem-se
 ≠ ≠
 no contradominio. no contradominio.
|
Pode haver elementos do contradominio que nao pertencam a imagem da funcao.
|
|
A funcao
    dada por dada por
 , e injetiva porque numeros distintos possuem dobros distintos. , e injetiva porque numeros distintos possuem dobros distintos.
|
Nem sempre, mas sempre admite inversa a esquerda.
|
| Sobrejetora ou sobrejetiva
|
Todos os elementos do contradominio estao associados a algum elemento do dominio.
|
O conjunto imagem e igual ao conjunto contradominio
|

|
A funcao
  , e sobrejetiva. , e sobrejetiva.
|
Nem sempre, mas sempre admite inversa a direita.
|
| Bijetora ou bijetiva
|
Sao ao mesmo tempo sobrejetoras e injetoras, isto e, cada elemento do dominio esta associado a um unico elemento do contradominio e vice-versa.
|
O conjunto imagem e igual ao conjunto contradominio
|

|
A funcao
  , e bijetiva. , e bijetiva.
|
Sim.
|
Dizemos que uma funcao
 e definida de forma explicita (funcao explicita) quando seus valores
e definida de forma explicita (funcao explicita) quando seus valores
 podem ser expressados pela variavel independente
podem ser expressados pela variavel independente
 i.e., quando temos uma relacao da forma
i.e., quando temos uma relacao da forma
 Por outro lado, dizemos que uma tal funcao e definida de forma implicita (funcao implicita) quando a relacao entre as variaveis dependente e independente e dada como
Por outro lado, dizemos que uma tal funcao e definida de forma implicita (funcao implicita) quando a relacao entre as variaveis dependente e independente e dada como
 onde
onde
 denota uma expressao envolvendo
denota uma expressao envolvendo
 e
e
 [
8
]
[
8
]
Seja
 dada por
dada por
 Isto e, a funcao que toma dois valores reais e os associa ao produto entre eles. Trata-se de uma funcao explicita. Agora, a equacao
Isto e, a funcao que toma dois valores reais e os associa ao produto entre eles. Trata-se de uma funcao explicita. Agora, a equacao
 define implicitamente a funcao
define implicitamente a funcao
 que associa um numero real nao nulo
que associa um numero real nao nulo
 ao seu inverso. Ou seja, tal funcao
ao seu inverso. Ou seja, tal funcao
 esta, aqui, definida implicitamente por
esta, aqui, definida implicitamente por
 Notamos que neste caso em particular, podemos definir a funcao
Notamos que neste caso em particular, podemos definir a funcao
 de forma explicita, escrevendo
de forma explicita, escrevendo

Dadas uma funcao

 e uma funcao
e uma funcao

 com
com
 definimos a funcao composta de
definimos a funcao composta de
 com
com
 por
por

 Analogamente, quando
Analogamente, quando
 tambem podemos definir a funcao composta de
tambem podemos definir a funcao composta de
 com
com
 dada por
dada por

 [
1
]
[
1
]
Considere as seguintes funcoes
 e
e
 dada por:
dada por:
 e
e

Notamos que
 e, portanto, podemos definir a funcao composta
e, portanto, podemos definir a funcao composta
 por:
por:

Tambem, como

temos a composicao

dada por:

Funcoes sao classificadas quanto a uma series de propriedades (caracteristicas) alem das ja mencionadas. Alguns desses tipos de funcoes sao listados a seguir.
O conceito matematico de funcao emergiu no seculo XVII em conexao com o desenvolvimento do
Calculo
.
[
9
]
[
10
]
O termo "funcao" foi introduzido por
Gottfried Leibniz
em uma de suas cartas, datada de 1673, na qual ele descreve a
declividade
de uma curva em um ponto especifico.
[
11
]
Na antiguidade, embora nao se conheca o uso explicito de funcoes, tal conceito pode ser observado em alguns trabalhos percursores de
filosofos
e
matematicos
medievais, como
Oresme
.
[
12
]
Matematicos do seculo XVII tratavam por funcoes aquelas definidas por
expressoes analiticas
.
[
13
]
Foi durante os desenvolvimentos rigorosos da
Analise Matematica
por
Weierstrass
e outros, a reformulacao da
Geometria
em termos da
analise
e a invencao da
Teoria dos Conjuntos
por Cantor, que se chegou ao conceito moderno e geral de uma funcao como um mapeamento univoco de um conjunto em outro. Nao ha consenso sobre a quem se deva os creditos da nocao moderna de funcao, sendo cotada os matematicos
Nikolai Lobachevsky
,
Peter Gustav Lejeune Dirichlet
e
Dedekind
.
[
14
]
[
15
]
[
16
]
Referencias
- ↑
a
b
c
d
e
Iezzi, Gelson (1977).
Fundamentos de Matematica Elementar: conjuntos e funcoes
. Sao Paulo: Atual. pp. 73?74A, 179A?180A
- ↑
STEWART, James. Calculo Vol. I - 4ª edicao. Sao Paulo: Pioneira Thomson Learning, 2002. Pagina 12.
- ↑
FRANK AYRES, Philip A. Schmidt. Matematica para Ensino Superior - 3ª edicao. Sao Paulo: Editora Artmed, 2003. Pagina 16.
- ↑
Nachtigall, Cicero; Molter, Alexandre; Zahn, Mauricio (2021).
Conjunto e Funcoes: Com aplicacoes
. Sao Paulo: Edgard Blucher
- ↑
a
b
c
Anton, Howard; Bivens, Irl; Davis, Srephen (2014).
Calculo: Volume I
. Porto Alegre: Bookman
- ↑
STEWART, James. Calculo Vol. I - 4ª edicao. Sao Paulo: Pioneira Thomson Learning, 2002.
- ↑
a
b
FRANK AYRES, Philip A. Schmidt. Matematica para Ensino Superior - 3ª edicao. Sao Paulo: Editora Artmed, 2003.
- ↑
Bronshtein, I.N. (2007).
Handbook of Mathematics
. Berlin: Springer. 120 paginas
- ↑
"The emergence of a notion of function as an individualized mathematical entity can be traced to the beginnings of infinitesimal calculus". (
Ponte 1992
)
- ↑
Kleiner, Israel (2009). ≪Evolution of the Function Concept: A Brief Survey≫. In: Marlow Anderson; Victor Katz; Robin Wilson.
Who Gave You the Epsilon?: And Other Tales of Mathematical History
. [S.l.]: MAA. pp. 14?26.
ISBN
978-0-88385-569-0
- ↑
Eves dates Leibniz's first use to the year 1694 and also similarly relates the usage to "as a term to denote any quantity connected with a curve, such as the coordinates of a point on the curve, the slope of the curve, and so on" (
Eves 1990
, p. 234).
- ↑
"...although we do not find in [the mathematicians of Ancient Greece] the idea of functional dependence distinguished in explicit form as a comparatively independent object of study, nevertheless one cannot help noticing the large stock of functional correspondences they studied." (
Medvedev 1991
)
- ↑
N. Bourbaki (18 de setembro de 2003).
Elements of Mathematics Functions of a Real Variable: Elementary Theory
. [S.l.]: Springer Science & Business Media. pp. 154?.
ISBN
978-3-540-65340-0
- ↑
"On the vanishing of trigonometric series," 1834 (
Lobachevsky 1951
).
- ↑
Uber die Darstellung ganz willkurlicher Funktionen durch Sinus- und Cosinusreihen," 1837 (
Dirichlet 1889
).
- ↑
"By a mapping φ of a set
S
we understand a law that assigns to each element
s
of
S
a uniquely determined object called the
image
of
s
, denoted as φ(
s
).
Dedekind 1995
- Avila, Geraldo Severo de Souza. (2005).
Analise matematica
para licenciatura
. Sao Paulo. Edgard Blucher.
ISBN 85-212-0371-3
.
- Barboni, Ayrton; Paulette, Walter. (2007).
Fundamentos de Matematica: Calculo e Analise
. Editora LTC.
ISBN 978-85-216-1546-0
.
- Iezzi, G; Murakami, C.. (2013).
Fundamentos de Matematica Elementar: Conjuntos e Funcoes
. vol. 1, 9. ed., Atual Editora:Sao Paulo.
ISBN 9788535716801
.