この記事には ?考文? や 外部リンク の一?が含まれていますが、 脚注 によって?照されておらず、情報源が不明瞭です 。 脚注を導入して、記事の 信?性向上 にご協力ください。 （ 2023年3月 ）

三角? （さんかくすう、 英 : triangular number ）とは、 多角? の一種で、点を 正三角形 の形に?べていったときの点の??のことである。 n 番目の三角?は 1 から n までの 自然? の 和 に等しい。

定義と例 [ 編集 ]

一?に n 個の 正三角形 となるように点を等間隔に?べたときの点の??は 1 から n までの 自然? の 和 に等しくなり、

${\displaystyle 1+2+3+\cdots +n={\frac {n(n+1)}{2}}\quad (n\geqq 1).}$

と表される。

これを n 番目の 三角? といい、 T _n で表す。三角?は無?にあり、最小のものは 1 である。

例えば 10 は一?に点を 4 個?べたときに該?するので三角?の一つである。

1		3		6		10		15		21

特に三角? 10 (= 1 + 2 + 3 + 4) は ピタゴラス （?派）にとって「完全なる?」として大事な?とされた。

${\displaystyle T_{n}=1+2+3+\cdots +n={\frac {n(n+1)}{2}}\quad (n\geqq 1).}$

において、 T ₀ = 0 と定義すると n = 0 のときも成り立つ。この式は下?のように、 n 番目の三角?を灰色の点の三角形と赤色の点の三角形でそれぞれ表し、2つの三角形を組み合わせると、高さ n , 底? n + 1 の長方形になり、その長方形の面積の半分として得ることができる。

2		6		12		20		30		42

三角?の列は次のようになる。

1 , 3 , 6 , 10 , 15 , 21 , 28 , 36 , 45 , 55 , 66 , 78 , 91 , 105 , 120 , 136 , 153 , 171 , 190 , 210 , 231 , 253 , 276 , 300 , 325 , 351 , 378 , 406 , 435 , 465 , 496 , 528 , 561 , 595 , 630 , 666 , 703 , 741 , 780 , 820 , … （ オンライン整?列大?典 の?列 A217 ）

類似の?係 [ 編集 ]

三角?を2倍した?を 矩形? （くけいすう）という。矩形?とは、行?（?に延びた列の?）と列?（?に延びた列の?）の差が 1 である 長方形 の形に点を?べていったときの、点の??のことである。すなわち、連?する2整?の積である。矩形とは 長方形 のことで、長方形?ということもある。

• n 番目の矩形?は、 n 番目までの正の 偶? の ?和 に等しい： ${\displaystyle \textstyle \sum \limits _{k=1}^{n}2k=n(n+1)}$

三角?と同?に 四角? （しかくすう）も定義される。これは、点を 正方形 の形に?べていったときの点の??のことである。これは 平方? に等しい。

• n 番目の四角?は、 n 番目までの正の 奇? の?和に等しい： ${\displaystyle \textstyle \sum \limits _{k=1}^{n}(2k-1)=n^{2}}$
• 連?する2つの三角?の和は 平方? （四角?）である： T _{n −1} + T _n = n ²

これを、 T _{n −1} を灰色の点、 T _n を赤色の点で表すと下?のようになる。

1		4		9		16		25		36

• n 番目の四角? n ² と n 番目の矩形? n ( n + 1) の和は 2 n 番目の三角? n (2 n + 1) に等しい。

各種の性質 [ 編集 ]

• 三角?は 組合せ 記?で表すことができる： T _n = _{n +1} C ₂
• n （ ≥ 2 ）チ?ムの??たりの リ?グ? における全試合の回?は T _{n −1} に等しい。
• 三角?は 3 で割り切れるか、もしくは 9 で割ると 1 余る?のどちらかである。
• 三角?に9を掛けて1を足した?もまた三角?である。
• 自然?の n までの 立方和 は T _n ² に等しい： ${\displaystyle \textstyle \sum \limits _{k=1}^{n}k^{3}=\left\{{\dfrac {n(n+1)}{2}}\right\}^{2}}$
• 三角?の 逆? 和は 2 に?束する。これは矩形?の逆?和 1 の 2 倍である：

${\displaystyle \textstyle \sum \limits _{n=1}^{\infty }{\dfrac {1}{\frac {n(n+1)}{2}}}=2\sum \limits _{n=1}^{\infty }\left({\dfrac {1}{n}}-{\dfrac {1}{n+1}}\right)=2}$

この 部分分?分解 から、三角?の逆?を 1 個、 2 個、 4 個、 ?? 2 の n （ ≥ 0 ) ?個、??ずつ順に加えてゆくと初項 1 , 公比 1/2 の無限 等比?列 になることが導かれる。

${\displaystyle {\frac {1}{1}}=1}$

${\displaystyle {\frac {1}{3}}+{\frac {1}{6}}={\frac {1}{2}}}$

${\displaystyle {\frac {1}{10}}+{\frac {1}{15}}+{\frac {1}{21}}+{\frac {1}{28}}={\frac {1}{4}}}$

…

• 三角?の 漸化式 として

T _{a + b} = T _a + T _b + ab や T _ab = T _a T _b + T _{a −1} T _{b −1} などが?げられる。

• 回文? である三角?は 55 , 66 , 666 だけであると考えられている。
• あらゆる自然?は 高? 3つの三角?の和で表すことができる、という定理がある。これは、 ガウス によって 1796年 （彼の日誌によれば 7月10日 ）に?明された。この定理は全ての自然?が高? n 個の n 角?の和で表すことができるという フェルマ?の多角?定理 の中に含まれている。
• 偶? の 完全? は三角?でもある。
• 平方?でもある三角?は 平方三角? と呼ばれ、無?にある。 1, 36 , 1225 , … （ オンライン整?列大?典 の?列 A001110 ）
• フィボナッチ? である三角?は 1 , 3 , 21 , 55 （ オンライン整?列大?典 の?列 A039595 ）
• 五角? である三角?は 1 , 210 , 40755, 7906276, … （ オンライン整?列大?典 の?列 A014979 ）
• 楔? である三角?は 66 , 78 , 105 , 190 , 231 , 406 , 435 , 465 , 561 , 595 , … （ オンライン整?列大?典 の?列 A128896 ）
• ハ?シャッド? である三角?は 1 , 3 , 6 , 10 , 21 , 36 , 45 , 120 , 153 , 171 , 190 , 210 , 300 , … （ オンライン整?列大?典 の?列 A076713 ）
• 等比三項の和 r ⁰ + r ¹ + r ² で表せる三角?は 3 , 21 , 91 , 703 , … （ オンライン整?列大?典 の?列 A069017 ）（ 0 ⁰ が定義できないので 1 は除外した。)
• 1 / 3 T _{3 n −1} は全て 五角? であり、 T _{2 n −1} は全て 六角? である。また六角?は全て三角?でもある。
• 中心つき多角?n は、三角?にnをかけて、1を加えた値になっている。

  ${\displaystyle 1+2=3}$

${\displaystyle 4+5+6=7+8}$

${\displaystyle 9+10+11+12=13+14+15}$

…

と無限に?く足し算の等式は タルタリアの三角形 と呼ばれる。上から n 段目の等式の値は n 番目の三角?の 2n + 1 倍である。1段目から n 段目までの?和は、1から n までの立方和（ n 番目の三角?の自?）の 1 + 2/n 倍であり、連?三角?の積である。

• ${\displaystyle 3^{2}+4^{2}=5^{2}}$

${\displaystyle 10^{2}+11^{2}+12^{2}=13^{2}+14^{2}}$

${\displaystyle 21^{2}+22^{2}+23^{2}+24^{2}=25^{2}+26^{2}+27^{2}}$

…

と無限に?く自?和の等式も同じ名で呼ばれる。上から n 段目の等式は 2n 番目の（六角?でない）三角?から 2n + 1 個の連??の自?項を左?で n + 1 個、右?で n 個足したものである。中央は n 番目の三角?の4倍の自?である。等式の値は1から n までの立方和の 16(n + 1/2) 倍と n 番目の 四角錐? の和に等しい。

• ${\displaystyle 1^{2}+1*3=2^{2}}$

${\displaystyle 6^{2}+7^{2}+6*10=8^{2}+9^{2}}$

${\displaystyle 15^{2}+16^{2}+17^{2}+15*21=18^{2}+19^{2}+20^{2}}$

…

上記のように自?和の三角形から漏れた?にも、足し算の三角形と興味深い?係がある。?ち 2n - 1 番目の三角?（ n 番目の六角?）から 2n 個の連??の n 個ずつの自?和の差は、足し算の三角形の1段目から 2n - 1 段目までの?和に等しく、連?三角?の積である。例えば 6 ² + 7 ² と 8 ² + 9 ² の差60は足し算の三角形の1段目から3段目までの?和に等しく、 6 × 10 である。また、自?和の三角形の順序を入れ換えると、次のように別の連?三角?の積が現れる。 n 段目の積は足し算の三角形の1段目から 2n 段目までの?和に等しく、足し算と自?和の三角形の n 段目の中央?の和に等しい。例えば2段目の 10 × 15 は足し算の三角形の1段目から4段目までの?和に等しく、 6 + 12 ² である。

• ${\displaystyle 3^{2}+5^{2}=4^{2}+3*6}$

${\displaystyle 10^{2}+12^{2}+14^{2}=11^{2}+13^{2}+10*15}$

${\displaystyle 21^{2}+23^{2}+25^{2}+27^{2}=22^{2}+24^{2}+26^{2}+21*28}$

…

三角?の判定 [ 編集 ]

?えられた自然? N が三角?であるには、 ${\displaystyle {\sqrt {8N+1}}}$ が整?であることが必要十分である。また

${\displaystyle n={\frac {{\sqrt {8N+1}}-1}{2}}}$

で?えられる n は N が n 番目の三角?を表している。この式は n についての 二次方程式 T _n = N の解である。

ゼロ以外の三角?の ?字根 は 1, 3, 6, 9 のいずれかである。したがって、?えられた自然? の?字根を計算してこれらでなければ N は三角?ではない。

5で割った余りが2または4であることは、三角?でないことを示すに十分である。

三角?の一般次元への?張 [ 編集 ]

点を配置する空間の 次元 を 3 にして、点を 正四面? （ 三角錐 ）?に配置したとき、その??を 三角錐? （四面??）という。第 n 三角錐?は、第 1 三角?から第 n 三角?までの ?和 であるが、その値を N とおくと ${\displaystyle N={\frac {n(n+1)(n+2)}{6}}}$ と書くことができる。また、同?に三角錐?の?和として、4次元空間での「三角?」（一般的に「 ?? ?」という） 五胞?? を定義することができる。以下、一般次元の空間（ここでは r 次元）まで?念の?張を行ったとき、第 n 番目の??? T _r ( n ) は

${\displaystyle T_{r}(n)=\textstyle \prod \limits _{k=1}^{r}\displaystyle \left(1+{\frac {n-1}{k}}\right)={\frac {n(n+1)\cdots (n+r-1)}{r!}}={\binom {n+r-1}{r}}={}_{n+r-1}{\rm {C}}_{r}}$

となる。

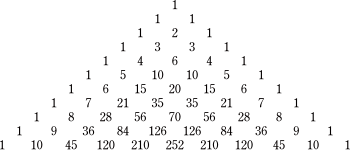パスカルの三角形 における ?列 は左上（または右上）にある列から順に:

• モナド（ ?? ）の?列　 1, 1, 1, 1, 1, 1, 1, 1, 1, …, _{n -1} C ₀ , …
• 自然?の?列 1, 2, 3, 4, 5, 6, 7, 8, 9, …, _n C ₁ , …
• 三角?の?列 1, 3, 6, 10, 15, 21, 28, 36, 45, …, _{n +1} C ₂ , …
• 三角錐?の?列 1, 4, 10, 20, 35, 56, 84, 120, 165, …, _{n +2} C ₃ , …
• 五胞??の?列 1, 5, 15, 35, 70, 126, 210, 330, 495, …, _{n +3} C ₄ , …

となっている。左上（または右上）にある?列はその1つ右下（または左下）の?列の 階差?列 である。

?考文? [ 編集 ]

• フロリアン?カジョリ 『 カジョリ 初等??史 』 小倉金之助 補?（復刻版）、共立出版〈共立全書〉、1997年6月。 ISBN   4-320-01538-X 。 http://www.kyoritsu-pub.co.jp/bookdetail/9784320015388 。  

?連項目 [ 編集 ]

外部リンク [ 編集 ]

• デジタル大?泉『 三角? 』 - コトバンク
• 『 三角?とは，三角?定理，平方?との?係 』 - 高校??の美しい物語
• Weisstein, Eric W. "Triangular Number" . mathworld.wolfram.com (英語).