U elementarnoj matematici i fizici , a napose u tehni?kim primjenama , vektor naj?e??e ozna?ava veli?inu koja ima iznos, smjer i orijentaciju, te zadovoljava pravila vektorskog ra?una. Taj se opis odnosi na veli?ine u trodimenzionalnom prostoru iz na?eg svakodnevnog iskustva, koji u matematici najbolje opisuje tzv. Euklidski prostor . Vektori su uvedeni kao slo?enije veli?ine od skalara ; skalari su u nevedenom kontekstu veli?ine koje imaju samo broj?anu vrijednost koja mo?e biti pozitivna, 0 ili negativna, tj. opisuju se jednim realnim brojem. Za opis vektora u trodimenzionalnom prostoru potrebna su tri realna broja - npr. jedan za iznos i dva za smjer i orijentaciju (kutovi koji određuju polo?aj u prostoru prema koordinatnim osima), ili tri skalarne komponente u koordinatnom sustavu. Jo? slo?enije veli?ine od vektora su tenzori , preciznije tenzori drugoga reda i vi?ih redova, koji se u trodimenzionalnom prostoru opisuju s 9, 27 ili vi?e brojeva. U tenzorskom opisu, skalari su tenzori nultoga reda, a vektori su tenzori prvoga reda.

Formalno i op?enito, međutim, pojam vektora se u matematici, pa i fizici, i u drugim primjenama, definira znatno apstraktnije. Pristup se naj?e??e temelji na definiciji vektorskog prostora iz linearne algebre gdje se koriste vi?edimenzionalni (pa i beskona?no dimenzionalni) prostori nad poljem realnih ili kompleksnih skalara. Ipak, i u te op?e definicije ugrađene su analogije s gore navedenim slu?ajem iz "obi?nog" trodimenzionalnog prostora. Ve?i dio ovoga ?lanka ukratko izla?e jedan od mogu?ih "matemati?kih" opisa u prostoru od n dimenzija, no mnogi su rezultati izravno primjenjljivi na "obi?ne" trodimenzionalne vektore.

Iako je to matemati?ko izlaganje "mek?e" od punog formalizma linearne algebre (nije posve op?enito, niti su formalno definirani svi kori?teni pojmovi), ono ni u tome obliku nije posve blisko i neposredno upotrebljivo za razumijevanje relevantnih koncepata u naj?e??im fizikalnim i tehni?kim primjenama (a oslanja se i na "matemati?ku" terminologiju i simbole koji nisu uobi?ajeni u tehnici). Zato se prije te "matemati?ke opcije" ukratko opisuje koncept koji je bli?i prakti?nom "tehni?kom" poimanju.

Operativni opis vektora za fizikalne i tehni?ke primjene [ uredi | uredi kod ]

Dok skalari imaju samo broj?anu vrijednost, vektori imaju iznos, smjer i orijentaciju. Iznos vektora je broj?ana vrijednost koja ne mo?e biti negativna (npr. iznos brzine je 5 m/s), a smjer i orijentaciju vektora mo?emo pokazati prstom (npr. gore, prema sjeveroistoku, itd). Preciznije, smjer je određen pravcem na kojemu le?i vektor, a orijentacija govori prema kojoj strani pravca je vektor orijentiran (kamo upu?uje vrh strelice u uobi?ajenom grafi?kom predo?avanju vektora). Takav je opis vektora ograni?en na opa?ajni trodimenzionalni prostor. Tu su vektorske veli?ine brzina , sila , ubrzanje , koli?ina gibanja ... a skalarne masa , temperatura , obujam .

Vektorska veli?ina obilje?ava se strelicom iznad simbola, npr. sila je ${\displaystyle \scriptstyle {\vec {F}}}$ (ili "masnim slovom", npr. F ), dok se njezin iznos obilje?ava istim obi?nim slovom, npr. iznos sile je ${\displaystyle \scriptstyle F}$, jer se iz konteksta zna da to slovo ozna?ava silu koja je vektorska veli?ina. (U matematici se iznos vektora mora ozna?iti vertikalnim crtama, npr. ${\displaystyle \scriptstyle |{\vec {F}}|}$ jer bi, op?enito, slovo ${\displaystyle \scriptstyle F}$ moglo ozna?avati neku skalarnu veli?inu koja nema veze s vektorima.)

Vektor se grafi?ki prikazuje pomo?u usmjerene du?ine (pomo?u du?ine koja ima strelicu na jednom kraju). Ona pokazuje smjer i orijentaciju vektora, a njezina duljina je proporcionalna iznosu vektora. Umjesto na?elne proporcionalnosti, iznos vektora mo?e se grafi?ki i precizirati, npr. tako da se nazna?i koliko njutna kod prikazane sile predstavlja 1 cm na skici. Neke se vektorske veli?ine doista i mjere u jedinicama za duljinu (npr. u centimetrima), pa ih usmjerena du?ina u cijelosti opisuje (npr. vektor polo?aja jo? zvan i radijvektor, te vektor pomaka).

Vektorske veli?ine u fizikalnim primjenama uglavnom su slobodni vektori ("pravi" vektori), no neke mogu biti vezani vektori ili pak klizni vektori . Primjerice, kad sila djeluje na deformabilno tijelo, njezin u?inak ovisi o tome u kojoj to?ki zahva?a tijelo: ona je vezani vektor (vezan za tu to?ku koja se zove hvati?te sile). Kad sila djeluje na kruto tijelo, njezin u?inak ovisi o pravcu na kojemu le?i, ali du? njega mo?e po volji "klizati", pa je klizni vektor. Zato silu prikazujemo kao usmjerenu du?inu koja "po?inje" (ili "zavr?ava") u svome hvati?tu. Drugi primjer vezanog vektora je vektor polo?aja koji je usmjerena du?ina povu?ena iz referentne to?ke (ishodi?ta).

No, prilikom razli?itih matemati?kih operacija sa silama i vektorima polo?aja (zbrajanje itd.), a kod ve?ine drugih vektorskih veli?ina ve? i u samom prikazu, svejedno je gdje se pozicionira usmjerena du?ina koja ih predstavlja: va?an je samo iznos, smjer i orijentacija. To je svojstvo "slobodnih" ili "pravih" vektora: ako se usmjerena du?ina translatira u prostoru, ona i dalje predstavlja isti vektor. Matemati?ki re?eno, vektor je klasa usmjerenih du?ina koje imaju isti iznos, smjer i orijentaciju. Vektor kojem je po?etak stavljen u izabranu to?ku tako je samo reprezentant (predstavnik) klase usmjerenih du?ina s obzirom na translacije.

Zbrajanje vektora [ uredi | uredi kod ]

Postupak zbrajanja vektora najlak?e je intuitivno razumjeti na primjeru zbrajanja sila po pravilu paralelograma, koji je navodno bio poznat jo? u anti?ko doba, a eksplicitno ga spominju i Galileo i Newton. ^[1]

U donjem dijelu lijeve skice prikazano je zbrajanje vektora ${\displaystyle \scriptstyle {\vec {u}}}$ i ${\displaystyle \scriptstyle {\vec {v}}}$ po pravilu paralelograma, a u gornjem dijelu isti rezultat je dobiven "nadovezivanjem" vektora. O?ito je da su rezultati jednaki, jer je prikazani trokut identi?an gornjoj polovici paralelograma (a jednako se mogla koristiti i donja polovica). Nadovezivanje mogu?uje jednostavnije zbrajanje ve?eg broja vektora (skica desno): nadovezuju se jedan na drugoga, a zbroj je usmjerena du?ina koja "ide" od po?etka prvoga do kraja zadnjega.

I u jednom i u drugom primjeru zbrajanja, vektori su prikazani usmjerenim du?inama koje se mogu po volji translatirati (paralelno premje?tati) a da pritom i dalje predstavljaju iste vektore. Kod zbrajanja po paralelogramu, usmjerene du?ine postavljaju se u istu po?etnu to?ku, a kod nadovezivanja po?etak druge se premje?ta u kraj prve. Va?no je uo?iti da rezultat ne ovisi o redoslijedu pribrojnika (zbrajanje vektora je komutativno), niti o njihovom grupiranju u slu?aju vi?e pribrojnika (zbrajanje vektora je asocijativno) zbog ?ega na skici desno nema zagrada u ispisu zbroja.

Neke veli?ine, kojima se osim iznosa mo?e pridru?iti i smjer, nisu vektori jer ne zadovoljavaju ta svojstva vektorskog ra?una. Primjerice, kutu zakreta mo?e se pridru?iti isti smjer koji ima (prosje?na) kutna brzina , ?to je vrlo prikladno za njegovo opisivanje u prostoru; ali kutovi zakreta nisu vektori, zato ?to njihov zbroj ovisi o redoslijedu zbrajanja.

Rastavljanje vektora na komponente je obrnuti postupak od zbrajanja. Npr. za paralelogram s lijeve skice mo?e se smatrati i da prikazuje rastav vektora ${\displaystyle \scriptstyle {\vec {u}}+{\vec {v}}}$ na komponente ${\displaystyle \scriptstyle {\vec {u}}}$ i ${\displaystyle \scriptstyle {\vec {v}}}$. Kao ?to rastav broja na pribrojnike nije jedinstven ( npr. broj 9 se mo?e rastaviti na 5+4 ali i na 6+3 ), tako to nije ni rastav vektora. U pravilu kod rastavljanja vektora na pribrojnike, tra?imo rastav na zbroj vektora ?iji su smjerovi unaprije poznati, ili koji zadovoljavaju neka posebna svojstva, poput međusobne okomitosti. Rastavljanje vektora na komponente ?esto je potrebno za razumijevanje njihove uloge, a i znatno olak?ava ra?un.

Mno?enje vektora skalarom; suprotni vektor [ uredi | uredi kod ]

Mno?enje vektora sa skalarom (brojem) je jednostavan postupak koji se intuitivno tuma?i na temelju zbrajanja vektora sa samim sobom: ${\displaystyle \scriptstyle {\vec {v}}+{\vec {v}}=2{\vec {v}}}$ (taj rezultat se dobiva nadovezivanjem vektora na samoga sebe). Odatle se lako razumije poop?enje: kod mno?enja sa skalarom, mno?i se samo iznos vektora apsolutnom vrijedno??u skalara, a rezultat je vektor istoga smjera i iste orijentacije ako je skalar pozitivan, odnosno vektor istog smjera i suprotne orijentacije ako je skalar negativan (skica desno). Specijalno, suprotni vektor od ${\displaystyle \scriptstyle {\vec {v}}}$ (vektor jednakog iznosa i smjera ali suprotne orijentacije) je vektor ${\displaystyle \scriptstyle -{\vec {v}}}$ koji se dobije mno?enjem vektora ${\displaystyle \scriptstyle {\vec {v}}}$ sa skalarom -1.

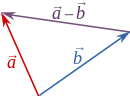Oduzimanje vektora [ uredi | uredi kod ]

Oduzimanje vektora ${\displaystyle \scriptstyle {\vec {b}}}$ od vektora ${\displaystyle \scriptstyle {\vec {a}}}$ isto je ?to i dodavanje suprotnog vektora, tj. ${\displaystyle \scriptstyle {\vec {a}}-{\vec {b}}={\vec {a}}+(-{\vec {b}})}$. Takav postupak grafi?ki je prikazan ni?e u "matemati?kom" dijelu teksta.

U mnogim prakti?nim primjenama, međutim, prikladnije je koristiti postupak prikazan na skici lijevo. Vektori na koje treba primijeniti oduzimanje grafi?ki se prika?u pomo?u usmjerenih du?ina povu?enih iz iste to?ke, a njihovu razliku prikazuje usmjerena du?ina koja spaja njihove vrhove i koja ima smjer prema onome vektoru od kojega se drugi oduzima.

Nije te?ko dokazati da usmjerena du?ina ${\displaystyle \scriptstyle {\vec {a}}-{\vec {b}}}$ doista jest tra?ena razlika: treba samo prinijeniti pravilo o zbrajanju vektora na prikazanu skicu. Skica se mo?e interpretirati kao da prikazuje zbrajanje vektora ${\displaystyle \scriptstyle {\vec {b}}+({\vec {a}}-{\vec {b}})}$, ?iji rezultat o?ito mora biti (kad se makne zgrada) jednak vektoru ${\displaystyle \scriptstyle {\vec {a}}}$, kao ?to crte? i pokazuje.

Komponente vektora [ uredi | uredi kod ]

Za mnoge primjene korisno je rastaviti vektorske veli?ine na komponente u koordinatnom sustavu. Na skici desno prikazan je rastav sile ${\displaystyle \scriptstyle {\vec {F}}}$ u Kartezijevom sustavu x,y na dvije komponente. Njezine vektorske komponente su vektori paraleni s koordinatnim osima, ${\displaystyle \scriptstyle {\vec {F}}_{x}}$ i ${\displaystyle \scriptstyle {\vec {F}}_{y}}$, tako da je:

${\displaystyle {\vec {F}}={\vec {F}}_{x}+{\vec {F}}_{y}}$.

Budu?i da su paralelne s koordinatnim osima, svaka od tih vektorskih komponenti mo?e se opisati brojem (skalarom), kojim treba pomno?iti jedini?ni vektor odgovaraju?e osi, ${\displaystyle \scriptstyle {\vec {i}}}$ ili ${\displaystyle \scriptstyle {\vec {j}}}$. Jedni?ni vektor ima iznos jednak jedinici i smjer pripadne osi, pa je:

${\displaystyle {\vec {F}}_{x}=F_{x}{\vec {i}}}$

${\displaystyle {\vec {F}}_{y}=F_{y}{\vec {j}}}$

a brojevi ${\displaystyle \scriptstyle F_{x}}$ i ${\displaystyle \scriptstyle F_{y}}$ zovu se skalarne komponente vektora du? osi x odnosno y . Na skici desno vidi se da je

${\displaystyle F_{x}=4N}$

${\displaystyle F_{y}=-2N}$

Iz tako zadanih skalarnih komponenti, iznos ${\displaystyle \scriptstyle F}$ vektora ${\displaystyle \scriptstyle {\vec {F}}}$ lako se izra?una pomo?u Pitagorinog pou?ka

${\displaystyle F={\sqrt {F_{x}^{2}+F_{y}^{2}}}}$

a smjer i orijentacija u ravnini x,y opisuju se pomo?u kuta prema jednoj od koordinatnih osi. Na skici je ozna?en kut prema osi x , na na?in uobi?ajen u tehni?koj praksi (za razliku od matematike), kao neorijentirani kut ${\displaystyle \scriptstyle \alpha }$ manji od 90°. Taj se kut mo?e odrediti pomo?u tangensa omjera skalarnih komponenti.

Obrnuto, ako bi bio poznat iznos vektora ${\displaystyle \scriptstyle {\vec {F}}}$ i kut ${\displaystyle \scriptstyle \alpha }$, skalarne komponente za primjer sa skice ra?unaju se kao

${\displaystyle F_{x}=F\cos \alpha }$

${\displaystyle F_{y}=-F\sin \alpha }$

gdje se predznak skalarne komponente određuje sa skice, jer su trigonometrijske funkcije kuta manjega od 90° pozitivne. Va?no je napomenuti da se u matematici kut koji vektor zatvara s x -osi obilje?ava u smjeru rotacije suprotne od kazaljke na satu. Na primjer, kut prikazan na slici, matemati?ki bi bio ozna?en negativnom vrijedno??u. Time se izbjegava pojavljivanje predznaka (kojeg ina?e treba bilje?iti ovisno o kontekstu) u prethodnim formulama.

U mnogim je prakti?nim situacijama mogu?e promatrati vektore i njihove komponente samo u jednoj ravnini, kao na gornjoj skici. No, ?esto promatrani vektori ne le?e u istoj ravnini, pa je potrebno ra?unati s njihovim komponentama du? sve tri osi (skica lijevo). Postupak rastavljanja na komponente u na?elu je sli?an, iako ima malo vi?e ra?unanja.

Vektor se pomo?u skalarnih komponenti mo?e zapisati na dva na?ina. Jedan je da se eksplicitno navedu jedni?ni vektori koordinatnih osi, kako slijedi iz prethodnog opisa:

${\displaystyle {\vec {F}}=F_{x}{\vec {i}}+F_{y}{\vec {j}}+F_{z}{\vec {k}}}$

Drugi na?in je pomo?u uređene trojke brojeva: navode se samo skalarne komponente u redoslijedu x,y,z  :

${\displaystyle {\vec {F}}=(F_{x},F_{y},F_{z})}$

U takvom zapisu, sila ${\displaystyle \scriptstyle {\vec {F}}}$ iz gornjeg ravninskog primjera prikazuje se kao

${\displaystyle {\vec {F}}=(4N,-2N,0)}$.

U op?enitijem matemati?kom opisu u n-dimenzionalnom prostoru, vektori se obi?no prikazuju pomo?u uređenih n-torki, a brojevi u njima nazivaju se komponentama ili koordinatama vektora u nekoj bazi prostora.

Prikaz vektora pomo?u skalarnih komponenti u na?em "obi?nom" prostoru zna?ajno olak?ava ra?unanje. Vektori su jednaki ako su im jednake odgovaraju?e skalarne komponente. Vektori se zbrajaju ili oduzimaju tako da se zbroje ili oduzmu njihove odgovaraju?e skalarne komponente. I druge operacije među vektorima izra?avaju se preko skalarnih komponenata, a razli?ite jednad?be među vektorima preslikavaju se u jednad?be među njihovim skalarnim komponentama.

Međusobno mno?enje vektora [ uredi | uredi kod ]

U na?em obi?nom prostoru, dva se vektora mogu međusobno mno?iti na dva na?ina, koji su se razvili ponajprije za potrebe jednostavnijeg zapisa odnosa među vektorskim veli?inama u fizici, napose u mehanici.

Skalarni produkt , ili skalarni umno?ak , ili unutarnji produkt , ili in-produkt (na engleskom dot product , jer se obi?no pi?e pomo?u to?ke između vektora) je operacija koja kao rezultat mno?enja dvaju vektora daje skalar (broj). Npr. za vektore ${\displaystyle \scriptstyle {\vec {a}}}$ i ${\displaystyle \scriptstyle {\vec {b}}}$ mo?e se skalarni produkt definirati jednostavnim izrazom:

${\displaystyle {\vec {a}}\cdot {\vec {b}}=ab\cos \theta }$,

gdje je ${\displaystyle \scriptstyle \theta }$ kut među vektorima, dok su ${\displaystyle \scriptstyle a}$ i ${\displaystyle \scriptstyle b}$ njihovi iznosi.

Vektorski produkt , ili vektorski umno?ak (jer se obi?no pi?e pomo?u kri?i?a sli?noga znaku znaku x ) je operacija koja kao rezultat mno?enja dvaju vektora (npr. vektora ${\displaystyle \scriptstyle {\vec {u}}}$ i ${\displaystyle \scriptstyle {\vec {v}}}$) daje tre?i vektor, smjera koji je okomit na smjerove vektora koje mno?imo, a orijentaciju mu određuje pravilo desne ruke (skica desno). Umno?ak (taj tre?i vektor) pi?e se kao ${\displaystyle \scriptstyle {\vec {u}}\times {\vec {v}}}$, a izos mu je:

${\displaystyle |{\vec {u}}\times {\vec {v}}|=uv\sin \theta }$,

Budu?i da je rezultat vektorskog mno?enje dvaju vektora opet vektor, on se mo?e dalje mno?iti s nekim vektorom. Ako je to daljnje mno?enje vektorsko, dobije se trostruki vektorski produkt , npr:

${\displaystyle ({\vec {u}}\times {\vec {v}})\times {\vec {w}}}$.

Rezultat ovisi o polo?aju zagrada (tj. vektorsko mno?enje nije asocijativno). Usto, za razliku od skalarnog mno?enja, treba paziti i na redoslijed faktora u vektorskom mno?enju, jer se zamjenom mjesta dobiva vektor suprotne orijentacije (vektorsko mno?enje je antikomutativno). Trostruki produkt mo?e se, naravno, i dalje vektorski mno?iti, pa se dobije ?etverostruki produkt, itd.

Ako se vektorski produkt dvaju vektora pomno?i skalarno s tre?im vektorom, dobije se tzv. mje?oviti produkt .

${\displaystyle {\vec {u}}\cdot ({\vec {v}}\times {\vec {w}})}$

Apsolutni iznos (dakle, vrijednost bez predznaka) koji se dobije mje?ovitim mno?enjem tri vektora geometrijski se interpretira (slika lijevo) kao volumen paralelopipeda (kose prizme s bazom paralelograma, tijela u prostoru razapetog s tri vektora).

Iznos vektorskog produkta je, po definiciji, jednak povr?ini paralelograma kojega određuju vektori ${\displaystyle \scriptstyle {\vec {v}}}$ i ${\displaystyle \scriptstyle {\vec {w}}}$ (obojan sivo, povr?ina ozna?ena slovom A ). Iznos skalarnog produkta vektora ${\displaystyle \scriptstyle {\vec {u}}}$ i ${\displaystyle \scriptstyle {\vec {v}}\times {\vec {w}}}$ jednak je umno?ku te povr?ine i projekcije vektora ${\displaystyle \scriptstyle {\vec {u}}}$ na vektor ${\displaystyle \scriptstyle {\vec {v}}\times {\vec {w}}}$, koja je ozna?ena slovom h . Dakle, rezultat mje?ovitog produkta je volumen prikazane kose prizme, V=Ah .

Neka va?na svojstva mno?enja vektora, kao i zapis mno?enja pomo?u skalarnih komponenata, navedeni su u "matemati?kom" dijelu koji slijedi.

Matemati?ka definicija vektora u n -dimenzionalnom prostoru [ uredi | uredi kod ]

Vektorske veli?ine su op?enito određene s vi?e broj?anih parametara. Najpoznatiji su primjeri vezani za geometriju u ravnini ili prostoru gdje se vektor određuje kao razred ekvivalencije usmjreneih du?ina ili alternativno smjerom (klasom ekvivalencije paralelnih pravaca), orijentacijom (smislom) i duljinom (iznosom, veli?inom, normom). Vizualno predstavlja strelicom orijentiranom du? pravca, duljine razmjerne veli?ini, a ?iji vrh pokazuje smjer na zadanom pravcu. Pojam vektora nije ograni?en na dvije ili tri dimenzije.

U n -dimenzionalnom realnom prostoru razlikujemo dvije vrste vektora. Vektore prve vrste obi?no zovemo usmjerenim (orijentiranim) du?inama ili u?vr??enim vektorima jer je njihova po?etna to?ka u?vr??ena (fiksna). Ti vektori su naprosto du?ine sa zadanom orijentacijom (smislom), odnosno kod kojih znamo koji kraj du?ine je po?etna (polazna), a koji je zavr?na to?ka. Dakle, u?vr??eni vektor je zadan uređenim parom to?aka (krajeva du?ine). Druga vrsta vektora koje zovemo to?nije slobodnim vektorima ili naprosto vektorima su razredi ekvivalencije usmjerenih du?ina gdje su dvije du?ine ekvivalentne ako se spojnica po?etka prve i kraja druge usmjerene du?ine i spojnica po?etka druge i kraja prve du?ine međusobno sijeku i raspolavljaju. To zna?i da su ekvivalentne usmjerene du?ine paralelne stranice paralelograma s međusobno jednakom orijentacijom.

Recimo da su to A i B iz R ⁿ . Tada komponente vektora ?iji su predstavnici usmjerene du?ine s tim krajevima imaju prikaz u komponentama (kao vektor-reci)

${\displaystyle {\overrightarrow {AB}}=\left(B_{1}-A_{1},B_{2}-A_{2},\dots ,B_{n}-A_{n}\right)}$,

${\displaystyle {\overrightarrow {BA}}=\left(A_{1}-B_{1},A_{2}-B_{2},\dots ,A_{n}-B_{n}\right)}$

(Slobodni) vektor je jednozna?no određen svojim smjerom, duljinom i orijentacijom. Vektore u?vr??ene u jednoj te istoj to?ki mo?emo međusobno zbrajati i mno?iti realnim brojem. Slobodne vektore mo?emo također zbrajati i mno?iti brojem (skalarom).

Svaki slobodni vektor ${\displaystyle {\overrightarrow {v}}}$ određuje jedinstvenu bijekciju ${\displaystyle A\mapsto A+{\overrightarrow {v}}}$, translaciju za vektor ${\displaystyle {\overrightarrow {v}}}$, takvo da je ${\displaystyle B=A+{\overrightarrow {v}}}$ onda i samo onda ako je usmjerena du?ina ${\displaystyle {\overrightarrow {AB}}}$ predstavnik vektora ${\displaystyle {\overrightarrow {v}}}$. Preslikavanje iz Abelove grupe svih slobodnih vektora vektorskog prostora u skup bijekcija prostora je djelovanje te grupe koje je slobodno i tranzitivno, tj. ?ini strukturu afinog prostora.

Neka su ${\displaystyle A\neq B}$ dvije to?ke u n -dimenzionalnom realnom prostoru. Funkcija iz skupa realnih brojeva u skup slobodnih vektora dana sa

${\displaystyle t\mapsto A+t{\overrightarrow {AB}}}$

je injekcija koja ima kao sliku cijeli pravac ${\displaystyle AB}$ koji sadr?i te to?ke. Ka?emo da ta funkcija ?ini parametrizaciju pravca ${\displaystyle AB}$ realnim brojevima. To je poseban slu?aj parametrizacije krivulje u prostoru. Ako umjesto vektora ${\displaystyle {\overrightarrow {AB}}}$ u gornjoj formuli stavimo ma koji nenul vektor proporcionalan (kolinearan) vektoru ${\displaystyle {\overrightarrow {AB}}}$ dobit ?emo isti pravac. Na primjer, ako uzmemo jedini?ni vektor ${\displaystyle {\frac {\overrightarrow {AB}}{\|{\overrightarrow {AB}}\|}}}$, tada govorimo o primjeru prirodne parametrizacije pravca u smislu da je duljina segmenta među dvjema to?kama na pravcu jednaka razlici vrijednosti parametra ${\displaystyle t}$ u tim dvjema to?kama. Su?enje funkcije ${\displaystyle t\mapsto A+t{\overrightarrow {AB}}}$ na samo pozitivne brojeve ili samo negativne brojeve parametrizira otvoreni (a ako dodamo i ${\displaystyle t=0}$ onda zatvoreni) polupravac s vrhom ${\displaystyle A}$.

Nul-vektor [ uredi | uredi kod ]

Nul-vektor a ₀ je vektor ?iji je intenzitet jednak nuli. Ozna?uje se kao nula s naznakom za vektor.

${\displaystyle {\overrightarrow {a_{0}}}={\overrightarrow {0}},\;|{\overrightarrow {a_{0}}}|=0}$

Jedini?ni vektor [ uredi | uredi kod ]

Jedini?ni je vektor vektor ?ija je veli?ina jednaka jedan. Za svaki se ne-nul vektor a mo?e odrediti odgovaraju?i jedini?ni vektor v iste orijentacije i smjera.

${\displaystyle {\overrightarrow {v}}={\frac {\overrightarrow {a}}{|{\overrightarrow {a}}|}},\;{\overrightarrow {a}}\neq {\overrightarrow {0}}}$

Ovaj se postupak zove normiranje vektora.

Operacije nad vektorima [ uredi | uredi kod ]

Nad vektorima se, kao i svim ostalim elementima analiti?ke matematike, mogu uvesti aritmeti?ke operacije. Pri tome se vektor predstavlja kao uređena n-torka skalara koji pripadaju nekom polju K . Na primjer:

${\displaystyle a=(a_{1},a_{2},a_{3},...,a_{n}),\;a_{i}\in K}$, ${\displaystyle i=1,...,n}$

je jedan n -dimenzionalni vektor nad poljem K . Pojam n -dimenzionalni dolazi od ?injenice da je vektor definiran pomo?u n skalara. Prostor ovih vektora se jo? naziva K ⁿ , a skalari koji ?ine vektor zajedno s informacijom o njihovoj poziciji u uređenoj n -torci koordinate vektora. Na primjer, a ₁ je prva koordinata vektora, a ₂ je druga koordinata vektora itd.

Slijede osnovne operacije nad vektorima, koje se u principu definiraju nad vektorima istih dimenzija.

Duljina vektora [ uredi | uredi kod ]

Duljina vektora (sinonimi: norma vektora, veli?ina vektora) se u euklidskoj geometriji je udaljenost među krajevima ma koje usmjerene du?ine koja je predstavnik tog vektora. Prema primjeni Pitagorinog pou?ka, u pravokutnom koordinatnom sustavu mo?emo duljinu vektora alternativno odrediti kao kvadratni korijen zbroja kvadrata njegovih komponenti.

${\displaystyle {\overrightarrow {a}}=(a_{1},a_{2},...,a_{n})\in K^{n}}$

${\displaystyle |a|={\sqrt {\sum _{k=1}^{n}{a_{i}}^{2}}}={\sqrt {a_{1}^{2}+a_{2}^{2}+...+a_{n}^{2}}}}$

Op?enitije, u ma kojem realnom vektorskom prostoru sa skalarnim umno?kom ${\displaystyle (,)}$, definiramo normu ${\displaystyle \|{\overrightarrow {v}}\|}$ vektora ${\displaystyle {\overrightarrow {v}}}$ kao

${\displaystyle \|v\|={\sqrt {(v,v)}}}$

Mno?enje vektora skalarom [ uredi | uredi kod ]

Mno?enje vektora ${\displaystyle {\overrightarrow {a}}\in K^{n}}$ nekim skalarom ${\displaystyle \alpha \in K}$ je definirano kao mno?enje svake koordinate vektora tim skalarom. Ova je operacija komutativna .

${\displaystyle \alpha \cdot {\overrightarrow {a}}}$ = ${\displaystyle \alpha \cdot (a_{1},a_{2},a_{3},...,a_{n})}$ = : ${\displaystyle (\alpha \cdot a_{1},\alpha \cdot a_{2},...,\alpha \cdot a_{n}).}$

Zbrajanje vektora [ uredi | uredi kod ]

Uzmimo dva vektora ${\displaystyle a,b\in K^{n}\,}$:

${\displaystyle {\overrightarrow {a}}=(a_{1},...,a_{n})}$

${\displaystyle {\overrightarrow {b}}=(b_{1},...,b_{n})}$

Njihovo se zbrajanje u principu definira kao zbrajanje komponenti s istim indeksima.

${\displaystyle +:(K^{n},K^{n})\rightarrow K^{n}\,}$

${\displaystyle {\overrightarrow {c}}={\overrightarrow {a}}+{\overrightarrow {b}}}$,

${\displaystyle c_{i}=a_{i}+b_{i}\,}$, gdje je ${\displaystyle i=1,...,n\,}$

Pri ?emu ?e vektor c biti iz prostora ${\displaystyle K^{n}\,}$. Oduzimanje vektora se provodi na sli?an na?in:

${\displaystyle {\overrightarrow {c}}={\overrightarrow {a}}+(-{\overrightarrow {b}})}$

Pri ?emu ${\displaystyle -{\overrightarrow {b}}=(-b_{1},-b_{2},...,-b_{n})}$.

Skalarno mno?enje vektora [ uredi | uredi kod ]

Sli?no zbrajanju, skalarno se mno?enje vektora definira kao broj umno?ka svih parova koordinata dva vektora, koje imaju iste indekse. Ovaj se zbroj i umno?ak preuzimaju iz polja K . Razlika u odnosu na zbrajanje je ta ?to je rezultat skalarnog produkta dva vektora iz K ⁿ u stvari jedan skalar iz K . Konkretno za dva vektora a i b iz K ⁿ bi umno?ak k izgledao ovako:

${\displaystyle \cdot :(K^{n},K^{n})\rightarrow K}$

${\displaystyle k={\overrightarrow {a}}\cdot {\overrightarrow {b}}}$, ${\displaystyle k\in K}$

${\displaystyle k=\sum _{i=1}^{n}{a_{i}\cdot b_{i}}}$, gdje je ${\displaystyle i=1,...,n}$

Ovdje treba primijetiti da je skalarni produkt vektora također jednak

${\displaystyle k={\overrightarrow {a}}\cdot {\overrightarrow {b}}=|a|\cdot |b|\cdot \cos \omega ,}$

pri ?emu je ω kut između a i b .

Ovo zapravo zna?i i:

${\displaystyle {\overrightarrow {a}}\cdot {\overrightarrow {b}}=0\Rightarrow {\overrightarrow {a}}\bot {\overrightarrow {b}}}$

To jest da su dva ne-nul vektora međusobno okomita ako i samo ako im je skalarni produkt jednak nuli.

Vektorski produkt [ uredi | uredi kod ]

Jo? jedan tip umno?ka karakteristi?an za trodimenzionalne euklidske prostore ( E ³ ) je vektorski produkt . Definira se na sljede?i na?in:

${\displaystyle \times :(E^{3},E^{3})\rightarrow E^{3}\,}$

${\displaystyle {\overrightarrow {a}},{\overrightarrow {b}}\in E^{3}}$

${\displaystyle {\overrightarrow {a}}\times {\overrightarrow {b}}={\begin{vmatrix}{\overrightarrow {i}}&{\overrightarrow {j}}&{\overrightarrow {k}}\\a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\end{vmatrix}}=}$

${\displaystyle {\overrightarrow {i}}(a_{2}b_{3}-a_{3}b_{2})-{\overrightarrow {j}}(a_{1}b_{3}-a_{3}b_{1})+{\overrightarrow {k}}(a_{1}b_{2}-a_{2}b_{1})=}$ ${\displaystyle {\begin{pmatrix}a_{2}b_{3}-a_{3}b_{2}\\a_{3}b_{1}-a_{1}b_{3}\\a_{1}b_{2}-a_{2}b_{1}\end{pmatrix}}}$

Jer su ${\displaystyle {\overrightarrow {i}}=(1,0,0)}$, ${\displaystyle {\overrightarrow {j}}=(0,1,0)}$ i : ${\displaystyle {\overrightarrow {k}}=(0,0,1)}$ vektori kanonske baze E ³ .

Kod vektorskog je produkta bitno primijetiti sljede?e osobine:

${\displaystyle {\overrightarrow {a}}\times {\overrightarrow {b}}\bot {\overrightarrow {a}},{\overrightarrow {b}}}$, tj. vektorski produkt dva vektora je okomit na njih same.

${\displaystyle |{\overrightarrow {a}}\times {\overrightarrow {b}}|=|a||b|\sin \omega }$, gdje je : ${\displaystyle \omega }$ kut između ova dva vektora. Ovo zapravo zna?i da je veli?ina vektorskog produkta dva vektora jednaka povr?ini paralelograma koga ?ine vektori koje mno?imo.

${\displaystyle {\overrightarrow {a}}\times {\overrightarrow {b}}=-({\overrightarrow {b}}\times {\overrightarrow {a}})}$, tj. vektorski produkt nije komutativan .

${\displaystyle (\alpha \cdot {\overrightarrow {a}})\times {\overrightarrow {b}}=\alpha ({\overrightarrow {a}}\times {\overrightarrow {b}})}$, gdje je ${\displaystyle \alpha \in E}$. Tj. vektorski produkt se lijepo pona?a prema mno?enju skalarom slijeva.

Mje?oviti produkt [ uredi | uredi kod ]

Mje?oviti produkt vektora je ternarna matemati?ka operacija koja uređenu trojku vektora iz E ³ preslikava u skalar iz E . Zapisuje se sa

${\displaystyle [{\overrightarrow {a}},{\overrightarrow {b}},{\overrightarrow {c}}]}$

A po definiciji je:

${\displaystyle [{\overrightarrow {a}},{\overrightarrow {b}},{\overrightarrow {c}}]=({\overrightarrow {a}}\times {\overrightarrow {b}})\cdot {\overrightarrow {c}}=}$ ${\displaystyle {\begin{vmatrix}a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\\c_{1}&c_{2}&c_{3}\end{vmatrix}},}$ : ${\displaystyle {\overrightarrow {a}},{\overrightarrow {b}},{\overrightarrow {c}}\in E^{3}}$

?to zna?i da je apsolutna vrijednost mje?ovitog produkta tri vektora jednaka volumenu paralelepipeda kojeg oni oblikuju. Slijede neka osnovna svojstva mje?ovitog produkta:

• ${\displaystyle [x,y,z]=-[y,x,z]}$
• ${\displaystyle [x,y,z]=[z,x,y]=[y,z,x]}$
• ${\displaystyle [\alpha x,y,z]=\alpha [x,y,z]}$
• ${\displaystyle [x+t,y,z]=[x,y,z]+[t,y,z]}$

Izvori [ uredi | uredi kod ]

Vidjeti također [ uredi | uredi kod ]

• Vektorski prostor
• Vektorsko polje