Se dice que un sistema cualquiera,
mecanico
,
electrico
,
neumatico
, etc., es un
oscilador armonico
si, cuando se deja en libertad fuera de su posicion de
equilibrio
, vuelve hacia ella describiendo oscilaciones
sinusoidales
, o sinusoidales amortiguadas en torno a dicha posicion estable.
 La masa colgada del resorte forma un oscilador armonico.
La masa colgada del resorte forma un oscilador armonico.
El ejemplo es el de una
masa
colgada a un
resorte
. Cuando se aleja la masa de su posicion de reposo, el resorte ejerce sobre la masa una
fuerza
que es
proporcional
al desequilibrio (distancia a la posicion de reposo) y que esta dirigida hacia la posicion de equilibrio. Si se suelta la masa, la fuerza del resorte acelera la masa hacia la posicion de equilibrio. A medida que la masa se acerca a la posicion de equilibrio y que aumenta su
velocidad
, la
energia potencial
elastica
del resorte se transforma en
energia cinetica
de la masa. Cuando la masa llega a su posicion de equilibrio, la fuerza sera cero, pero como la masa esta en movimiento, continuara y pasara del otro lado. La fuerza se invierte y comienza a frenar la masa. La energia cinetica de la masa va transformandose ahora en energia potencial del resorte hasta que la masa se para. Entonces este proceso vuelve a producirse en direccion opuesta completando una oscilacion.
Si toda la energia cinetica se transformase en energia potencial y viceversa, la oscilacion seguiria eternamente con la misma amplitud. En la realidad, siempre hay una parte de la energia que se transforma en otra forma, debido a la
viscosidad
del aire o porque el resorte no es perfectamente elastico. Asi pues, la amplitud del movimiento disminuira mas o menos lentamente con el paso del tiempo. Se empezara tratando el caso ideal, en el cual no hay perdidas. Se analizara el caso
unidimensional
de un unico oscilador (para la situacion con varios osciladores, vease
movimiento armonico complejo
).
Oscilador armonico sin perdidas
[
editar
]
Se denominara
 a la distancia entre la posicion de equilibrio y la masa, a la que se le dominara
a la distancia entre la posicion de equilibrio y la masa, a la que se le dominara
 . Se supondra que la fuerza del resorte es estrictamente proporcional al desequilibrio:
. Se supondra que la fuerza del resorte es estrictamente proporcional al desequilibrio:
 (
ley de Hooke
).
(
ley de Hooke
).
 es la fuerza y
es la fuerza y
 la
constante elastica
del resorte. El signo negativo indica que cuando
la
constante elastica
del resorte. El signo negativo indica que cuando
 es positiva la fuerza esta dirigida hacia las
es positiva la fuerza esta dirigida hacia las
 negativas.
negativas.
La
segunda ley de Newton
nos dice:

remplazando la fuerza obtenemos:

La solucion de esta
ecuacion diferencial ordinaria
es inmediata: las unicas
funciones
reales
(no
complejas
) cuya segunda
derivada
es la misma funcion con el signo invertido son
seno
y
coseno
. Las dos funciones corresponden al mismo movimiento. Escogemos arbitrariamente "coseno". La solucion se escribe:
 La curva de arriba da la posicion del oscilador en funcion del tiempo. La del medio da la velocidad. Abajo estan las curvas de las energias. En azul esta la energia cinetica
La curva de arriba da la posicion del oscilador en funcion del tiempo. La del medio da la velocidad. Abajo estan las curvas de las energias. En azul esta la energia cinetica
 y en rojo la energia potencial del resorte
y en rojo la energia potencial del resorte


| Simbolo
|
Nombre
|

|
Elongacion o diferencia respecto al estado de equilibrio
|

|
Amplitud, maxima diferencia respecto a la posicion de equilibrio
|

|
Pulsacion
(o frecuencia angular)
|

|
Frecuencia
|

|
Tiempo
|

|
Fase
inicial (para
 ) )
|

Es facil comprobar que el valor de
 es:
es:
 El
periodo de oscilacion
es:
El
periodo de oscilacion
es:
 Como ya hemos dicho, durante un cuarto de una oscilacion la energia potencial se transforma en energia cinetica. Durante otro cuarto, la energia cinetica se transforma en energia potencial. En la figura de la derecha se ha trazado la posicion en funcion del tiempo (curva de arriba), la velocidad en funcion del tiempo (en medio) y las energias potenciales y cineticas (abajo).
Como ya hemos dicho, durante un cuarto de una oscilacion la energia potencial se transforma en energia cinetica. Durante otro cuarto, la energia cinetica se transforma en energia potencial. En la figura de la derecha se ha trazado la posicion en funcion del tiempo (curva de arriba), la velocidad en funcion del tiempo (en medio) y las energias potenciales y cineticas (abajo).
Oscilador armonico amortiguado
[
editar
]
 Oscilador armonico con amortiguador. La fuerza viscosa es proporcional a la velocidad.
Oscilador armonico con amortiguador. La fuerza viscosa es proporcional a la velocidad.
Es el caso de
rozamientos
secos: la fuerza no depende ni de la velocidad ni de la posicion. Otra situacion que se produce en la realidad es que la fuerza sea proporcional a la velocidad elevada a una
potencia
, entera o no. Asi sucede cuando la fuerza que frena proviene de la viscosidad o de las perdidas
aerodinamicas
. Se tratara unicamente el caso mas simple, es decir, cuando la fuerza sea proporcional a la velocidad. En este caso la fuerza sera:

Donde
 es un
coeficiente
que mide el amortiguamiento debido a la viscosidad. Si
es un
coeficiente
que mide el amortiguamiento debido a la viscosidad. Si
 es pequeno, el sistema esta poco amortiguado. Notese el signo negativo que indica, como antes, que si la velocidad es positiva, la fuerza tiene la direccion superior opuesta a la velocidad de la particula. Con este termino complementario la ecuacion diferencial del sistema es:
es pequeno, el sistema esta poco amortiguado. Notese el signo negativo que indica, como antes, que si la velocidad es positiva, la fuerza tiene la direccion superior opuesta a la velocidad de la particula. Con este termino complementario la ecuacion diferencial del sistema es:

Se trata de una ecuacion diferencial
ordinaria
,
lineal
, de segundo orden
[
1
]
(contiene derivadas segundas) y
homogenea
(no hay termino independiente de
 ). Tiene tres tipos de soluciones segun el valor de
). Tiene tres tipos de soluciones segun el valor de
 :
:
- Si
 el sistema esta sobreamortiguado (amortiguamiento fuerte o supercritico)
el sistema esta sobreamortiguado (amortiguamiento fuerte o supercritico)
- Si
 el sistema tiene amortiguamiento critico.
el sistema tiene amortiguamiento critico.
- Si
 el sistema oscila con amplitud decreciente (amortiguamiento debil o subcritico)
el sistema oscila con amplitud decreciente (amortiguamiento debil o subcritico)
Oscilador sobreamortiguado
[
editar
]
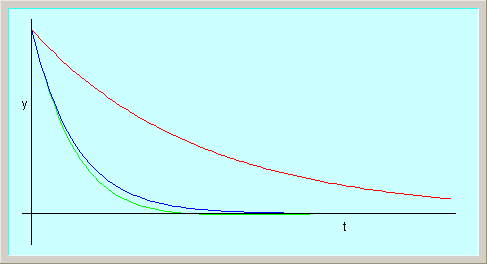 Posicion en funcion del tiempo de un oscilador armonico amortiguado.
Posicion en funcion del tiempo de un oscilador armonico amortiguado.
| curva azul: amortiguamiento critico.
|
| curva roja: amortiguamiento doble que el critico.
|
| curva verde: amortiguamiento igual a 90% del amortiguamiento critico.
|
En este caso el sistema no es realmente un oscilador, ya que no oscila. La solucion es de la forma:

donde los coeficientes de las exponenciales son menores que cero y reales (por lo que no hay oscilacion):

y

 y
y
 dependen de las condiciones iniciales (es decir, de la situacion del sistema para
dependen de las condiciones iniciales (es decir, de la situacion del sistema para
 ).
La posicion no es oscilante y tiende hacia la posicion de equilibrio de manera
asintotica
. Las dos exponenciales decrecientes de las soluciones tienen constantes de tiempo diferentes. Una es pequena
).
La posicion no es oscilante y tiende hacia la posicion de equilibrio de manera
asintotica
. Las dos exponenciales decrecientes de las soluciones tienen constantes de tiempo diferentes. Una es pequena
 y corresponde a la rapida cancelacion del efecto de la velocidad inicial. La segunda
y corresponde a la rapida cancelacion del efecto de la velocidad inicial. La segunda
 es mas grande y describe la lenta tendencia hacia la posicion de equilibrio.
es mas grande y describe la lenta tendencia hacia la posicion de equilibrio.
Oscilador con amortiguamiento critico
[
editar
]
Este caso es el limite entre un sistema oscilante y uno no oscilante. Ocurre cuando

La solucion unica es:

como antes,
 y
y
 son constantes que dependen de las condiciones iniciales.
son constantes que dependen de las condiciones iniciales.
El amortiguamiento critico corresponde a la tendencia mas rapida hacia la situacion de equilibrio cuando no sobrepasa esa posicion. Si se disminuye un poco el amortiguamiento el sistema se acerca mas rapidamente a la posicion de equilibrio, pero sobrepasando la posicion oscila en torno a ese punto (tomando valores positivos y negativos).
Oscilador con amortiguamiento debil
[
editar
]
 Oscilaciones amortiguadas. La amplitud de la sinusoide esta controlada por la exponencial.
Oscilaciones amortiguadas. La amplitud de la sinusoide esta controlada por la exponencial.
En este caso, que es mas interesante, tenemos un oscilador que oscila alrededor de la posicion de equilibrio con amplitud decreciente. Sucede cuando:

La solucion es:

como antes,
 y
y
 son constantes que dependen de las condiciones iniciales. La pulsacion es:
son constantes que dependen de las condiciones iniciales. La pulsacion es:

La pulsacion del sistema amortiguado es un poco menor que la pulsacion del sistema no amortiguado
 porque la fuerza que lo amortigua, frena la masa y la retarda.
porque la fuerza que lo amortigua, frena la masa y la retarda.
La oscilacion del sistema esta descrita por una sinusoide de frecuencia
 cuya amplitud esta multiplicada por una exponencial decreciente cuya constante de tiempo es
cuya amplitud esta multiplicada por una exponencial decreciente cuya constante de tiempo es
 .
.
Factor de calidad Q
[
editar
]
En un sistema poco amortiguado es conveniente definir el
factor de calidad'
(
Q
uality factor
en ingles), denotado por
Q
, como:

Esta cantidad es igual a
 veces el inverso de las perdidas relativas de energia por periodo. Asi, un sistema que pierde 1% de energia a cada ciclo, tendra un
Q
de 628. Mas interesante,
Q
es tambien
veces el inverso de las perdidas relativas de energia por periodo. Asi, un sistema que pierde 1% de energia a cada ciclo, tendra un
Q
de 628. Mas interesante,
Q
es tambien
 veces el numero de oscilaciones que el sistema hace mientras su amplitud decrece por un factor
veces el numero de oscilaciones que el sistema hace mientras su amplitud decrece por un factor
 . Aceptando una aproximacion mas burda,
Q
es 3 veces el numero de oscilaciones que un sistema hace mientras su amplitud cae a 1/3 de la amplitud inicial.
. Aceptando una aproximacion mas burda,
Q
es 3 veces el numero de oscilaciones que un sistema hace mientras su amplitud cae a 1/3 de la amplitud inicial.
Como ejemplos, el Q de un vehiculo con los
amortiguadores
en buen estado es algo mayor que 1. El Q de una cuerda de guitarra es de varios miles. El Q de los cristales de
cuarzo
utilizados en
electronica
como referencia de frecuencia es del orden de 1 millon. Una copa de
vidrio
ordinario tiene un Q mucho mas pequeno que una copa de
vidrio de plomo
(cristal).
Oscilaciones forzadas
[
editar
]
Podemos iniciar el movimiento un oscilador armonico desplazandolo de su posicion de equilibrio y abandonandolo a su oscilacion libre (ver parrafos precedentes).
Alternativamente, podemos aplicarle una fuerza cuya intensidad varie de manera sinusoidal con el tiempo. En esta situacion, la ecuacion diferencial lineal no es homogenea. La solucion a este tipo de ecuacion consta de dos terminos: la solucion general del sistema homogeneo mas una solucion particular del caso inhomogeneo.
[
2
]
Por tanto, la solucion tiene dos partes: una parte transitoria (que se anula pasado cierto tiempo), similar a las que vimos en los parrafos precedentes, y una parte estacionaria. La solucion de la parte transitoria es la misma la que ya hemos visto (ecuacion homogenea). Las unicas diferencias son las condiciones iniciales y finales, que no son identicas. Vamos a interesarnos por la solucion estacionaria. En la ecuacion diferencial del sistema hay que anadir la fuerza sinusoidal:

Para resolver esta ecuacion utilizaremos el mismo metodo que en electricidad y electronica. Para ello, se anade a la fuerza real una fuerza
imaginaria
 . Como en electronica, se utiliza la notacion
. Como en electronica, se utiliza la notacion
 en lugar de
i
. Ahora la ecuacion a resolver es:
en lugar de
i
. Ahora la ecuacion a resolver es:

Pero por supuesto, como en electricidad, solo la parte real de
 sera de interes.
La solucion es inmediata:
sera de interes.
La solucion es inmediata:

Si se deriva esta expresion y se sustituye en la ecuacion diferencial, se encuentra el valor de A:

Pero A puede escribirse como
 y la solucion de
y la solucion de
 compleja es:
compleja es:

El valor de
 real es la parte real de la expresion precedente:
real es la parte real de la expresion precedente:

donde
 es el
modulo
de
es el
modulo
de
 y
y
 su
argumento
:
su
argumento
:


Como en electricidad, el angulo
 da el
desfase
del movimiento con respecto a la fuerza externa. Si
da el
desfase
del movimiento con respecto a la fuerza externa. Si
 es positivo, el movimiento tiene la fase adelantada y si
es positivo, el movimiento tiene la fase adelantada y si
 es negativo el movimiento tiene la fase retrasada. En este caso el desfase sera siempre negativo.
es negativo el movimiento tiene la fase retrasada. En este caso el desfase sera siempre negativo.
Respuesta en frecuencia
[
editar
]
La amplitud de las oscilaciones forzadas dependera, por supuesto, de la amplitud de la fuerza externa. Pero para una misma amplitud de la fuerza, la amplitud de la oscilacion dependera tambien de la frecuencia. Veamos como varia la amplitud
 con
con
 . Utilizando la definicion de frecuencia propia del sistema (sin amortiguamiento ni fuerza externa):
. Utilizando la definicion de frecuencia propia del sistema (sin amortiguamiento ni fuerza externa):
 Respuesta en frecuencia de un oscilador armonico. A la frecuencia de resonancia, la amplitud es Q veces mas grande que a muy baja frecuencia.
Respuesta en frecuencia de un oscilador armonico. A la frecuencia de resonancia, la amplitud es Q veces mas grande que a muy baja frecuencia.

se puede escribir:

Si ademas se utiliza la definicion de
 , se obtiene:
, se obtiene:

En el dibujo de derecha se ha representado la amplitud de la oscilacion forzada en funcion de la frecuencia para varios valores del
factor de calidad
Q. A muy baja frecuencia la amplitud es la misma que si la fuerza fuese estatica
 , y el sistema oscilara entre las posiciones
, y el sistema oscilara entre las posiciones
 y
y
 . Cuando la frecuencia aumenta, la amplitud tambien, alcanzando un maximo cuando la frecuencia de excitacion es igual a la frecuencia propia del sistema. A esa frecuencia propia tambien se le llama
frecuencia de resonancia
. Tambien se dice que un sistema excitado a una frecuencia proxima a la frecuencia de resonancia "resuena" o "entra en resonancia". A la frecuencia de resonancia, la amplitud de las oscilaciones sera
Q
veces mas grande que la que se obtiene en baja frecuencia.
. Cuando la frecuencia aumenta, la amplitud tambien, alcanzando un maximo cuando la frecuencia de excitacion es igual a la frecuencia propia del sistema. A esa frecuencia propia tambien se le llama
frecuencia de resonancia
. Tambien se dice que un sistema excitado a una frecuencia proxima a la frecuencia de resonancia "resuena" o "entra en resonancia". A la frecuencia de resonancia, la amplitud de las oscilaciones sera
Q
veces mas grande que la que se obtiene en baja frecuencia.
El ancho del pico de resonancia a media altura, es decir cuando la amplitud es igual a la mitad del maximo, es igual a la frecuencia de resonancia dividida por
Q
. Ese ancho tambien se llama
banda pasante
.
Oscilador forzado y caos
[
editar
]
El oscilador armonico no perturbado en una dimension es un ejemplo de sistema integrable, con comportamiento regular. Sin embargo, el oscilador armonico perturbado puede presentar un comportamiento
caotico
[
3
]
caracterizado por un
atractor extrano
. Por ejemplo en el caso de una perturbacion de tipo
 la
ecuacion de movimiento
es:
la
ecuacion de movimiento
es:

Este sistema es no integrable y el movimiento tiende rapidamente hacia el llamado atractor de Duffing.
[
4
]
Oscilador de van der Pol
[
editar
]
 Comportamiento
caotico
en el oscilador de van der Pol con excitacion sinusoidal.
μ
= 8.53, mientras que la excitacion externa tiene amplitud
A
= 1.2 y frecuencia angular
ω
= 2π / 10.
Comportamiento
caotico
en el oscilador de van der Pol con excitacion sinusoidal.
μ
= 8.53, mientras que la excitacion externa tiene amplitud
A
= 1.2 y frecuencia angular
ω
= 2π / 10.
El
oscilador de van der Pol
es un caso especial de oscilador con amortiguamiento no lineal, que responde a la ecuacion:

Fue descrito por primera vez en 1935 por
Balthasar van der Pol
[
5
]
y presenta comportamiento caotico.
Oscilador armonico torsional
[
editar
]
Importancia en fisica
[
editar
]
Considerese el caso de un cuerpo sometido a una fuerza unidimensional:
 . Desarrollando dicha fuerza en
serie de Taylor
alrededor del punto de equilibrio (
. Desarrollando dicha fuerza en
serie de Taylor
alrededor del punto de equilibrio (
 ):
):

Como el origen es el punto de equilibrio, el primer termino del desarrollo es nulo. Si las oscilaciones en torno a
 son lo suficientemente pequenas, uno se puede quedar con la aproximacion lineal y despreciar los terminos de orden superior:
son lo suficientemente pequenas, uno se puede quedar con la aproximacion lineal y despreciar los terminos de orden superior:

Llamandole
 a la derivada de la fuerza, se obtiene de nuevo la fuerza recuperadora de Hooke. Aqui radica la importancia del oscilador armonico: supone una primera aproximacion para el estudio de un sistema cuando se producen pequenas oscilaciones en torno a su posicion (o estado) de equilibrio.
[
6
]
a la derivada de la fuerza, se obtiene de nuevo la fuerza recuperadora de Hooke. Aqui radica la importancia del oscilador armonico: supone una primera aproximacion para el estudio de un sistema cuando se producen pequenas oscilaciones en torno a su posicion (o estado) de equilibrio.
[
6
]
Ejemplos
[
editar
]
Circuito LC
[
editar
]
Circuito LC sin perdidas
[
editar
]
 Circuito LC sin perdidas.
Circuito LC sin perdidas.
En la figura de la derecha se ha dibujado un
circuito oscilante LC
(una bobina y un condensador) ideal, es decir sin perdidas.
Supongase que, en la situacion inicial, el
condensador
esta cargado a una
tension
V y que en ese momento se conecta la
inductancia
. La tension presente en las extremidades de la inductancia va a hacer aparecer una
corriente
de sentido inverso a la de la flecha del dibujo, que aumentara con el tiempo. A medida que el condensador suministra corriente a la inductancia, se descarga y la tension disminuye. La disminucion de la tension hace que la corriente aumente menos rapidamente. La situacion continua asi, con la tension del condensador que disminuye cada vez mas rapidamente (porque la corriente aumenta) y la corriente que aumenta mas lentamente (porque la tension disminuye). Llega un momento en el cual el condensador esta completamente descargado y la corriente ha llegado a un maximo.
Ahora la corriente continua circulando porque la inductancia se lo impone. El condensador comienza a cargarse en el otro sentido y hace aparecer una tension en los
bornes
de la inductancia que hace disminuir la corriente. La situacion continua del siguiente modo: el condensador se va cargando cada vez mas lentamente (porque la corriente disminuye), mientras que la corriente va disminuyendo cada vez mas rapidamente (porque la tension inversa aumenta). Asi, se llega a la situacion en la cual la corriente se anula y la tension del condensador es maxima y del mismo valor que la tension inicial, pero con sentido opuesto. La situacion es analoga a la de una masa sostenida por un resorte. La inductancia juega el papel de la masa. La masa tiene inercia e impide que el movimiento cambie bruscamente. La inductancia impide que la corriente cambie bruscamente. Veamos las ecuaciones.
El comportamiento electrico del condensador esta descrito por la ecuacion:
 . El de la inductancia esta descrito por
. El de la inductancia esta descrito por
 . Como en el esquema
. Como en el esquema
 es positivo cuando sale del lado positivo de la inductancia, hay que agregar un signo negativo:
es positivo cuando sale del lado positivo de la inductancia, hay que agregar un signo negativo:
 . Se tiene, pues, este sistema de ecuaciones diferenciales:
. Se tiene, pues, este sistema de ecuaciones diferenciales:


Para eliminar
 , basta derivar la primera ecuacion, para reemplazar la derivada de
, basta derivar la primera ecuacion, para reemplazar la derivada de
 en la segunda:
en la segunda:

que se puede escribir como:

Esta ecuacion es la misma que la de la masa con un resorte.
 es equivalente a la posicion
es equivalente a la posicion
 .
.
 es equivalente a la masa
es equivalente a la masa
 y
y
 es equivalente a la constante del resorte
es equivalente a la constante del resorte
 .
.
La solucion es:

con

Como de costumbre,
 y
y
 dependen de las condiciones iniciales.
dependen de las condiciones iniciales.
Circuito LC con perdidas
[
editar
]
 Circuito LC con perdidas. La resistencia da cuenta de todas la perdidas posibles.
Circuito LC con perdidas. La resistencia da cuenta de todas la perdidas posibles.
El esquema de la derecha representa un
circuito oscilante LC con perdidas
. Las perdidas estan representadas por las perdidas en una
resistencia
. En un circuito real, las perdidas provienen de resistencias en serie como la dibujada. Dichas resistencias pueden estar en el exterior de la inductancia o del condensador, pero tambien pueden ser resistencias internas de esos componentes. Tambien puede haber resistencias en paralelo, perdidas en el
dielectrico
del condensador o en el nucleo de la
bobina
(si es
ferromagnetico
). Tambien puede haber perdidas por
radiacion
de
ondas electromagneticas
. La resistencia hara que la tension sobre la bobina sea diferente de la tension sobre el condensador. La corriente creada sera menor que si no hubiese habido perdidas y cuando la corriente cargue de nuevo el condensador, la tension a la cual llegara sera menor. Por su parte, la amplitud disminuira y tendera hacia cero. La ecuacion del nuevo sistema es:

La ecuacion es la misma que la de una masa con un resorte y con un amortiguador. Esta vez
 es el equivalente del coeficiente de rozamiento
es el equivalente del coeficiente de rozamiento
 .
La solucion es:
.
La solucion es:

con

y

donde
 es la frecuencia propia del circuito (sin perdidas).
es la frecuencia propia del circuito (sin perdidas).
Oscilaciones forzadas de un circuito LC con perdidas
[
editar
]
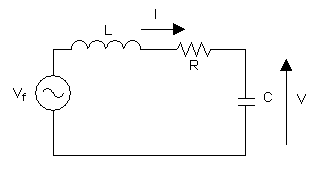 Circuito LRC atacado por un generador sinusoidal.
Circuito LRC atacado por un generador sinusoidal.
El esquema de la derecha muestra un generador conectado a un circuito LC en serie. Si la tension del generador es
 , la ecuacion es:
, la ecuacion es:

La expresion se puede reescribir, dandole un aspecto similar a las formas precedentes:

Como en el ejemplo mecanico, en regimen estacionario la solucion es:

donde

y

 y
y
 son los mismos que en el parrafo precedente.
La amplitud de la tension de salida es maxima a la resonancia (cuando
son los mismos que en el parrafo precedente.
La amplitud de la tension de salida es maxima a la resonancia (cuando
 ) y vale
) y vale
 veces la tension de entrada.
veces la tension de entrada.
Oscilador armonico cuantico
[
editar
]
 Funciones de onda para los primeros seis autoestados,
n
= 0 a 5. El eje horizontal muestra la posicion
y
en unidades (h/2πmω)
1/2
. Las graficas estan sin normalizar.
Funciones de onda para los primeros seis autoestados,
n
= 0 a 5. El eje horizontal muestra la posicion
y
en unidades (h/2πmω)
1/2
. Las graficas estan sin normalizar.
 Densidades de probabilidad de los primeros autoestados (dimension vertical, con los de menor energia en la parte inferior) para las diferentes localizaciones espaciales (dimension horizontal).
Densidades de probabilidad de los primeros autoestados (dimension vertical, con los de menor energia en la parte inferior) para las diferentes localizaciones espaciales (dimension horizontal).
Susodichamente, el oscilador armonico se puede emplear para estudiar sistemas que realicen pequenas oscilaciones en torno a una posicion de equilibrio. En particular, el
oscilador armonico cuantico
se puede emplear para estudiar las oscilaciones de los atomos de una molecula diatomica, como la de
hidrogeno
, H
2
, o la de
cloruro de hidrogeno
, HCl.
[
7
]
El oscilador armonico es uno de los casos en los que se puede obtener una solucion analitica sencilla de la
ecuacion de Schrodinger
. En esta situacion, el
hamiltoniano
de la particula considerada estara descrito por:

Notese que para el caso de moleculas diatomicas, la masa
 seria, en realidad, la
masa reducida
del sistema. Se ve claramente que el primer sumando es un termino cinetico, mientras que el segundo es el armonico. Como el hamiltoniano no depende del tiempo, solo resta resolver la ecuacion de Schrodinger independiente del tiempo, a fin de hallar los
autoestados
de la energia
seria, en realidad, la
masa reducida
del sistema. Se ve claramente que el primer sumando es un termino cinetico, mientras que el segundo es el armonico. Como el hamiltoniano no depende del tiempo, solo resta resolver la ecuacion de Schrodinger independiente del tiempo, a fin de hallar los
autoestados
de la energia
 :
:

Se puede demostrar que las
funciones de onda
,
 , cuyo modulo al cuadrado describe la
densidad de probabilidad
de que la particula tenga una determinada posicion
, cuyo modulo al cuadrado describe la
densidad de probabilidad
de que la particula tenga una determinada posicion
 , son el producto de exponenciales por los
polinomios de Hermite
. La figura de la derecha muestra la forma de dichas funciones para los seis autoestados con energia mas baja (el estado de menor energia es el que figura en la parte superior de la misma). En particular, la energia del nivel n-esimo sera:
, son el producto de exponenciales por los
polinomios de Hermite
. La figura de la derecha muestra la forma de dichas funciones para los seis autoestados con energia mas baja (el estado de menor energia es el que figura en la parte superior de la misma). En particular, la energia del nivel n-esimo sera:

donde
 es la
constante de Planck
.
es la
constante de Planck
.
Es importante senalar un par de hechos:
- Los niveles de energia se encuentran
cuantizados
, es decir, solo pueden tomar una serie de valores
discretos
.
- El nivel minimo de energia no es cero, sino
 . Notese que la funcion de onda de dicho estado muestra que la particula no se encuentra en todo momento en la posicion de equilibrio
. Notese que la funcion de onda de dicho estado muestra que la particula no se encuentra en todo momento en la posicion de equilibrio
 .
.
En la segunda figura, se muestran las densidades de probabilidad espacial de la particula para los diferentes autoestados. Notese que a medida que crece la energia del autoestado considerado (es decir, el orden
 ), las distribuciones de probabilidad tienden a concentrarse en los puntos de retorno, o maxima amplitud. Esta situacion es la que se da en el caso clasico, si se define para el una densidad de probabilidad inversamente proporcional a la velocidad de la particula en cada punto.
[
8
]
Por tanto, se cumple el
principio de correspondencia
(es decir, se pueden predecir los resultados que se obtendrian en el limite clasico).
), las distribuciones de probabilidad tienden a concentrarse en los puntos de retorno, o maxima amplitud. Esta situacion es la que se da en el caso clasico, si se define para el una densidad de probabilidad inversamente proporcional a la velocidad de la particula en cada punto.
[
8
]
Por tanto, se cumple el
principio de correspondencia
(es decir, se pueden predecir los resultados que se obtendrian en el limite clasico).
Vease tambien
[
editar
]
Referencias
[
editar
]
- ↑
Simmons, capitulo 3
- ↑
Simmons, paginas 84-87
- ↑
T.N. Palmer (1995): "A local deterministic model of Quantum Spin Measurement",
Proceedings: Mathematical and Physical Sciences
, Volume
451
, Issue 1943, pp. 585-608
- ↑
Atractor de Duffing
- ↑
Cartwright, M.L.,
"Balthazar van der Pol"
,
J. London Math. Soc.
,
35
, 367-376, (1960).
- ↑
Marion, paginas 103 y 104
- ↑
Tipler, pagina 1190
- ↑
Guillen, paginas 114 y 115
Bibliografia
[
editar
]
- Feynman, Leighton and Sands (1964).
Lectures on physics
. Addison-Wesley.
ISBN 0-8053-9045-6
.
- R. Resnick and D. Halliday (1996).
Physics
. John Wiley & Sons.
ISBN 0-471-83202-2
.
- Marion, Jerry B. (1996).
Dinamica clasica de las particulas y sistemas
. Barcelona: Ed. Reverte.
ISBN 84-291-4094-8
.
- Simmons, George F. (1999).
Ecuaciones Diferenciales. Con aplicaciones y notas historicas
. Aravaca (Madrid): McGraw-Hill.
ISBN 84-481-0045-X
.
- Tipler, Paul A. (2000).
Fisica para la ciencia y la tecnologia (volumen 2)
. Barcelona: Ed. Reverte.
ISBN 84-291-4382-3
.
- Sanchez Guillen, Joaquin. Braun, Mijail A. (1993).
Fisica cuantica
. Madrid: Alianza Editorial.
ISBN 84-206-8145-8
.
Enlaces externos
[
editar
]