En
matematicas
, un
conjunto numerable
es un
conjunto
o bien finito o bien del mismo tamano que los
numeros naturales
. Mas concretamente, un conjunto se dice que es numerable (o contable) cuando es finito o cuando existe una
biyeccion
entre este conjunto y el conjunto de los numeros naturales.
En 1874
Georg Cantor
introdujo el termino
conjunto numerable
, contrastando conjuntos que son contables con los que son
incontables
. Hoy en dia, los conjuntos numerables forman la base de una rama de las matematicas llamada
matematica discreta.
Definicion
[
editar
]
Un conjunto
 es
contable
si existe una
funcion inyectiva
es
contable
si existe una
funcion inyectiva
 desde
numeros naturales
desde
numeros naturales

 ya que existe una obvia biyeccion entre
ya que existe una obvia biyeccion entre
 y
y
 , no existe diferencia si se considera el 0 como natural o si no; en cualquier caso, este articulo toma la convencion estandar de la
logica matematica
, en donde se toma al
, no existe diferencia si se considera el 0 como natural o si no; en cualquier caso, este articulo toma la convencion estandar de la
logica matematica
, en donde se toma al

 a
a
 , es decir, a cada n de los naturales (dominio o conjunto de partida) le corresponde un elemento de S (imagen o conjunto de llegada) mediante una funcion
, es decir, a cada n de los naturales (dominio o conjunto de partida) le corresponde un elemento de S (imagen o conjunto de llegada) mediante una funcion
 .
.

Si la funcion
 llega a ser tambien sobreyectiva (y por lo tanto
biyectiva
), entonces
llega a ser tambien sobreyectiva (y por lo tanto
biyectiva
), entonces
 se llama infinito numerable.
se llama infinito numerable.
En otras palabras, un conjunto es infinito numerable si tiene
correspondencia uno a uno
con el conjunto de los numeros naturales
 .
.
Como se senalo anteriormente, esta terminologia no es universal. Algunos autores utilizan contable en el sentido de lo que aqui se llama
infinito numerable
, y no incluyen los conjuntos finitos.
Formulaciones alternativas (equivalentes) de la definicion en terminos de una funcion biyectiva o una funcion sobreyectiva tambien se puede dar. Vease abajo.
Historia
[
editar
]
En 1874, en su
primer articulo de la teoria de conjuntos
,
Cantor
demostro que el conjunto de los
numeros reales
es incontable, mostrando entonces que no todos los conjuntos infinitos son numerables.
[
1
]
En 1878 utilizo las correspondencias uno a uno para definir y comparar las
cardinalidades
.
[
2
]
En 1883 extendio los numeros naturales con sus
ordinales
infinitos, y uso conjuntos de ordinales para producir una infinidad de conjuntos teniendo diferentes cardinalidades infinitas.
[
3
]
Origen del termino
[
editar
]
La nocion de numerabilidad fue introducida por
Georg Cantor
en un articulo de 1874,
[
4
]
Sobre una propiedad del sistema de todos los numeros algebraicos reales
[
5
]
donde establece por una parte que el conjunto de
numeros algebraicos
reales (es decir, el conjunto de los numeros reales que son solucion de alguna
ecuacion polinomica
con coeficientes racionales) es numerable,
[
6
]
y por otra que el conjunto de todos los numeros reales no lo es, a partir de lo cual deduce inmediatamente la existencia de
numeros trascendentes
o no algebraicos, redescubriendo asi un
resultado de Liouville
.
Su origen esta ligado a la concepcion del infinito en matematicas. Hasta el descubrimiento de Cantor, el infinito era el
infinito potencial
, la posibilidad de continuar un proceso sin detenerse nunca. La comparacion de conjuntos infinitos trae consigo la nocion de
infinito alcanzado
, actual o completo: un conjunto infinito visto como un todo, un concepto que ha sido rechazado por numerosos matematicos (
Gauss
, o, en la epoca de Cantor,
Kronecker
, etc.).
[
7
]
Para ellos, el hecho de considerar una infinidad de objetos como un todo, es decir, el concepto de
conjunto
infinito no tiene sentido, sino que el infinito solo puede surgir del proceso de enumeracion sin repeticion que nunca se detiene. Solo el infinito numerable puede tener en rigor algun sentido.
Introduccion
[
editar
]
Un
conjunto
es una coleccion de
elementos
, y puede ser descrito de muchas maneras. Una forma es simplemente una lista de todos sus elementos; Por ejemplo, el conjunto que consiste en los numeros enteros 3, 4, y 5 puede ser denotado {3, 4, 5}. Esto solo es efectivo para pequenos conjuntos, sin embargo; para conjuntos mas grandes, esto podria llevar mucho tiempo y ser propenso a errores. En lugar de enumerar cada elemento, a veces se utilizan unos puntos suspensivos ("...") si el escritor cree que el lector puede adivinar facilmente lo que falta; por ejemplo, {1, 2, 3, ..., 100} presumiblemente denota el conjunto de los
enteros
de 1 a 100. Incluso en este caso todavia es
posible
listar todos los elementos, ya que el conjunto es
finito
.
Algunos conjuntos son
infinitos
; estos conjuntos tienen mas de
n
elementos para cualquier numero entero
n
. Por ejemplo, el conjunto de numeros naturales, escrito como {0, 1, 2, 3, 4, 5, ...}, tiene un numero infinito de elementos, y no podemos utilizar cualquier
numero normal
para dar su tamano. Sin embargo, resulta que los conjuntos infinitos tienen una idea bien definida de tamano (o mejor dicho, de
cardinalidad
, que es el termino tecnico para el numero de elementos en un conjunto), y no todos los conjuntos infinitos tienen la misma cardinalidad.
 Representacion biyectiva de enteros a numeros iguales.
Representacion biyectiva de enteros a numeros iguales.
Para entender lo que esto significa, primero examinamos
lo que no quiere decir
. Por ejemplo, hay un numero infinito de enteros impares, un numero infinito de enteros pares, y (por lo tanto) un numero infinito de numeros enteros en general. Sin embargo, resulta que el numero de enteros pares, que es el mismo que el numero de enteros impares, es tambien el mismo que el numero de enteros en general. Esto se debe a que para cada entero impar, existe un homologo, entero par: ... -2 → -4, -1 → -2, 0 → 0, 1 → 2, 2 → 4, ... En la imagen estan dispuestos los numeros enteros y los numeros pares en una
correspondencia uno-a-uno
(o
biyeccion
), que es una
funcion
que representa dos conjuntos de tal manera que cada elemento de cada conjunto corresponde a un solo elemento en el otro conjunto.
Sin embargo, no todos los conjuntos infinitos tienen la misma cardinalidad. Por ejemplo,
Georg Cantor
(que introdujo este concepto) demostro que los numeros reales no se pueden corresponder uno-a-uno con los numeros naturales (enteros no negativos), y por lo tanto, el conjunto de los numeros reales tiene una cardinalidad mayor que el conjunto de los numeros naturales.
Un conjunto es
numerable
si: (1) es finito, o (2) si tiene la misma cardinalidad (tamano) que el conjunto de los numeros naturales. De manera equivalente, un conjunto es
numerable
si tiene la misma cardinalidad que algun
subconjunto
del conjunto de los numeros naturales. De lo contrario, es
incontable
.
Formulacion general sin detalles
[
editar
]
Por definicion, un conjunto
S
es
numerable
si existe una
funcion inyectiva
f
:
S
→
N
desde
S
al conjunto de los
numeros naturales
N
= {0, 1, 2, 3, ...}.
Podria parecer normal dividir los conjuntos en diferentes clases: poner todos los conjuntos que contienen un elemento juntos; todos los conjuntos que contienen dos elementos juntos; ...; por ultimo, poner juntos todos los conjuntos infinitos y considerar que tienen el mismo tamano. Este punto de vista no es sostenible dentro de la definicion natural de tamano.
Para elaborar esto necesitamos el concepto de
biyeccion
. Aunque una
biyeccion
parece un concepto mas avanzado que un numero, el desarrollo habitual de las matematicas en terminos de la teoria de conjuntos define funciones antes de los numeros, ya que se basan en conjuntos mucho mas simples. Aqui es donde el concepto de biyeccion interviene: define la correspondencia
- a
↔ 1,
b
↔ 2,
c
↔ 3
Esto define una biyeccion, puesto que cada elemento de {
a
,
b,c
} se empareja con
un preciso elemento
de {1, 2, 3} , y viceversa.
Ahora se generaliza esta situacion y
definimos
dos conjuntos del mismo tamano si (y solo si) hay una biyeccion entre ellos. Para todos los conjuntos finitos esto nos da la definicion usual de
tamano equivalente
. ¿Que nos dice sobre el tamano de los conjuntos infinitos?
Considere los conjuntos
A
= {1, 2, 3, ...}, el conjunto de los
enteros
positivos y
B
= {2, 4, 6, ...}, el conjunto de los enteros positivos pares. Afirmamos que, bajo nuestra definicion, estos conjuntos tienen el mismo tamano, y que, por tanto,
B
es infinito numerable. Recordemos que para probar esto tenemos que probar una biyeccion entre ellos. Pero esto es facil, usando
n
↔ 2
n
, de modo que
- 1 ↔ 2, 2 ↔ 4, 3 ↔ 6, 4 ↔ 8, ....
Como en el ejemplo anterior, cada elemento de A se ha emparejado con un elemento de B y viceversa. De ahi que tengan el mismo tamano. Este es un ejemplo de un conjunto del mismo tamano que uno de sus subconjuntos propios (algo imposible para conjuntos finitos).
Del mismo modo, el conjunto de todos los
pares ordenados
de los numeros naturales es infinito numerable, como puede verse siguiendo una trayectoria como la de la imagen:
 La
Funcion de emparejamiento de Cantor
asigna un numero natural a cada par de los numeros naturales.
La
Funcion de emparejamiento de Cantor
asigna un numero natural a cada par de los numeros naturales.
La representacion resultante es:
- 0 ↔ (0,0), 1 ↔ (1,0), 2 ↔ (0,1), 3 ↔ (2,0), 4 ↔ (1,1), 5 ↔ (0,2), 6 ↔ (3,0) ....
Esta representacion abarca a todos los pares ordenados.
Curiosamente, si trata a cada par como el
numerador
el y
denominador
de una
fraccion vulgar
, a continuacion, para cada fraccion positiva, podemos llegar a una cantidad distinta que correspondera a la misma. Esta representacion incluye tambien a los numeros naturales, ya que cada numero natural es tambien una fraccion
N
/1. Por lo tanto podemos concluir que hay exactamente tantos numeros racionales positivos como numeros enteros positivos. Esto es cierto tambien para todos los numeros racionales, como puede verse a debajo.
Teorema:
El
producto cartesiano
de un numero finito de conjuntos numerables es numerable.
A veces mas de una representacion es util. Aqui es donde se representa que el conjunto que se desea mostrar es infinito numerable en otro conjunto, y luego representa este otro conjunto de los numeros naturales. Por ejemplo, los
numeros racionales
positivos pueden ser facilmente asignados a (un subconjunto de) los pares de numeros naturales porque
p
/
q
representa a (
p
,
q
).
¿Y que ocurre con los subconjuntos infinitos de los conjuntos numerables infinitos? ¿Tienen estos menos elementos que
N
?
Teorema:
Cada subconjunto de un conjunto numerable es numerable. En particular, cada subconjunto infinito de un conjunto infinito numerable es infinito numerable.
Por ejemplo, el conjunto de los
numeros primos
es contable, mediante la asignacion del
n-
esimo numero primo a
n
:
- El 2 representa al 1
- El 3 representa al 2
- El 5 representa al 3
- El 7 representa al 4
- El 11 representa al 5
- El 13 representa al 6
- El 17 representa al 7
- El 19 representa al 8
- El 23 representa al 9
- ...
¿Que ocurre con los conjuntos que son naturalmente "mayores que"
N
? Por ejemplo, el conjunto de los
enteros
,
Z
, o el conjunto de los numeros
racionales
,
Q
, que, intuitivamente puede parecer mucho mas grande que
N
. Pero las apariencias enganan, ya que afirmamos que:
Teorema:
Z
(el conjunto de todos los enteros) y
Q
(el conjunto de todos los numeros racionales) son contables.
De una manera similar, el conjunto de los
numeros algebraicos
es contable.
[
8
]
Teorema:
Cualquier
union
finita de conjuntos contables es contable.
Q
puede definirse como el conjunto de todas las fracciones del tipo
a'/
b
donde
a
y
b
son numeros enteros, con
b
> 0. Esto se puede corresponder con el subconjunto de triples ordenados de numeros naturales (
a
,
b
,
c
) de tal manera que si
a
≥ 0 y
b
> 0,
a
y
b
son coprimos, y
c
∈ {0, 1} luego
c
= 0 si
a
/
b
≥ 0, y
c
= 1 en caso contrario.
- El 0 representa a (0,1,0)
- El 1 representa a (1,1,0)
- El ?1 representa a (1,1,1)
- El 1/2 representa a (1,2,0)
- El ?1/2 representa a (1,2,1)
- El 2 representa a (2,1,0)
- El ?2 representa a (2,1,1)
- El 1/3 representa a (1,3,0)
- El ?1/3 representa a (1,3,1)
- El 3 representa a (3,1,0)
- El ?3 representa a (3,1,1)
- El 1/4 representa a (1,4,0)
- El ?1/4 representa a (1,4,1)
- El 2/3 representa a (2,3,0)
- El ?2/3 representa a (2,3,1)
- El 3/2 representa a (3,2,0)
- El ?3/2 representa a (3,2,1)
- El 4 representa a (4,1,0)
- El ?4 representa a (4,1,1)
- ...
Con la prevision de saber que hay conjuntos numerables, podemos preguntarnos si este ultimo resultado puede ser ampliado. La respuesta es "si" y "no", podemos extenderlo, pero tenemos que asumir un nuevo axioma para hacerlo.
Teorema:
(Asumiendo el
axioma de la eleccion numerable
) La union de una cantidad numerable de conjuntos numerables es numerable.
Por ejemplo, dado el conjunto numerable
a
,
b
,
c
, ...
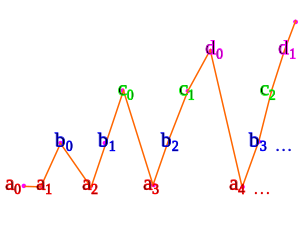 Enumeracion de numero contables de conjuntos numerables.
Enumeracion de numero contables de conjuntos numerables.
Usando una variante de la enumeracion triangular vista anteriormente:
- a
0
representa al 0
- a
1
representa al 1
- b
0
representa al 2
- a
2
representa al 3
- b
1
representa al 4
- c
0
representa al 5
- a
3
representa al 6
- b
2
representa al 7
- c
1
representa al 8
- d
0
representa al 9
- a
4
representa al 10
- ...
Tenga en cuenta que esto solo funciona si los conjuntos
a
,
b
,
c
, ... son conjuntos
disjuntos
. Si no es asi, entonces la union es aun mas pequena y por lo tanto tambien enumerable mediante uno de los teoremas anteriores.
Tambien tenga en cuenta que necesitamos el
axioma de la eleccion contable
para indexar
todos
los conjuntos
a
,
b
,
c
, ... simultaneamente.
Teorema:
El conjunto de todas las secuencias de longitud finita de numeros naturales es contable.
Este conjunto es la union de
secuencias
de longitud 1, longitud 2, longitud 3, las cuales son conjuntos numerables (producto cartesiano finito). Asi que estamos hablando de una union numerable de conjuntos numerables, que es contable por el teorema anterior.
Teorema:
El conjunto de todos los
subconjuntos
finitos de los numeros naturales es contable.
Teniendo un subconjunto finito, se pueden ordenar los elementos en una secuencia finita. Solo hay una cantidad numerable de secuencias finitas, por lo que tambien hay solo una cantidad numerable de subconjuntos finitos.
El siguiente teorema proporciona formulaciones equivalentes en terminos de una funcion biyectiva o
sobreyectiva
. Una prueba de este resultado se puede encontrar en el texto de Lang.
Teorema (basico):
Sea
S
un conjunto. Los siguientes enunciados son equivalentes:
- S
es contable, es decir, existe una funcion inyectiva
f
:
S
→
N
.
- O
S
esta vacio o existe una funcion sobreyectiva
g
:
N
→
S
.
- O
S
es finita o existe una
biyeccion
h
:
N
→
S
.
El teorema de Cantor
afirma que si
A
es un conjunto y
P
(
A
) es su
conjunto potencia
, es decir, el conjunto de todos subconjuntos de
a
, entonces no hay ninguna funcion sobreyectiva de
A
a
P
(
A
). Una prueba se da en el articulo del
teorema de Cantor
. Como consecuencia inmediata de esto y el teorema basico anterior tenemos:
Proposicion:
El conjunto
P
(
N
) no es contable; es decir, es
incontable
.
Para una elaboracion de este resultado vease el
argumento diagonal de Cantor.
El conjunto de los
numeros reales
es incontable (ver
primera prueba de incontabilidad de Cantor
), y tambien lo es el conjunto de todas las
secuencias
infinitas de los numeros naturales.
Algunos detalles tecnicos
[
editar
]
Las pruebas de las declaraciones contenidas en el apartado anterior se basan en la existencia de funciones con ciertas propiedades. Esta seccion presenta las funciones mas utilizadas en este papel, pero no la comprobacion de que estas funciones tienen las propiedades requeridas. El teorema basico a menudo se utiliza para simplificar las pruebas. Observe que
N
en este teorema puede ser sustituido por cualquier conjunto infinito numerable.
Proposicion:
Cualquier
conjunto finito
es contable.
Prueba:
Por definicion, existe una biyeccion entre un conjunto finito no vacio,
S
, y el conjunto {1, 2, ...,
n
} para cualquier numero natural positivo
n
. Esta funcion es una inyeccion de
S
en
N
.
Proposicion:
Cualquier subconjunto de un conjunto numerable es numerable.
[
9
]
Prueba
: La restriccion de una funcion inyectiva a un subconjunto de su
dominio
sigue siendo inyectiva.
Proposicion:
Si
S
es un conjunto numerable y
x
?
S
, entonces
S
∪ {
x
} es numerable.
[
10
]
Prueba:
Sea
f
:
S
→
N
una inyeccion, se define
g
:
S
∪ {
x
} →
N
como
g
(
x
) = 0
y
g
(
y
) =
f
(
y
) + 1
para toda
y
en
S
. Esta funcion
g
es una inyeccion.
Proposicion:
Si
A
y
B
son conjuntos numerables, entonces
A
∪
B
son numerable.
[
11
]
Prueba:
Sean
f
:
A
→
N
y
g
:
B
→
N
inyecciones, se define una nueva inyeccion
h
:
A
∪
B
→
N
como
h
(
x
) = 2
f
(
x
)
si
x
esta en
A
y
h
(
x
) = 2
g
(
x
) + 1
si
x
esta en
B
pero no en
A
.
Proposicion:
El
producto cartesiano
de dos conjuntos numerables
A
y
B
es numerable.
[
12
]
Prueba:
Observe que
N
×
N
es contable por definicion porque la funcion
f
:
N
×
N
→
N
dada por
f
(
m
,
n
) = 2
m
3
n
es inyectiva.
[
13
]
Entonces sigue el teorema basico del producto cartesiano, donde dos conjuntos numerables cualesquiera tienen un producto numerable. Si
A
y
B
son contables, existen subyecciones
f
:
N
→
A
y
g
:
N
→
B
. Asi que
- f
×
g
:
N
×
N
→
A
×
B
es una subyeccion de un conjunto numerable
N
×
N
al conjunto
A
×
B
y el corolario implica que
A
×
B
es contable. Este resultado generaliza el producto cartesiano de cualquier coleccion finita de conjuntos numerables y la demostracion por
induccion
del numero de conjuntos en la coleccion.
Proposition:
Los
enteros
Z
son contables y los numeros
racionales
Q
son contables.
Prueba:
Los enteros
Z
son contables debido a la funcion
f
:
Z
→
N
dada por
f
(
n
) = 2
n
si
n
no es negativo
f
(
n
) = 3
?
n
si
n
es negativo, es una funcion inyectiva. Los numeros racionales
Q
son contables debido a la funcion
g
:
Z
×
N
→
Q
dada por
g
(
m
,
n
) =
m
/(
n
+ 1)
es una subyeccion del conjunto numerable
Z
×
N
ha los racionales
Q
.
Proposition:
Los numeros algebraicos
A
son numerables.
Prueba:
Ya que todos los numeros algebraicos (incluyendo a los numeros complejos) son raices de un polinomio. Sea un polinomio
 , y el numero algebraico
, y el numero algebraico
 es la
k-
esima raiz del polinomio (En primer lugar, ordenados por
valor absoluto
de menor a mayor, a continuacion, ordenados por el argumento de menor a mayor). Podemos definir una funcion inyectiva (es decir, una a una)
f
:
A
→
Q
dada por
es la
k-
esima raiz del polinomio (En primer lugar, ordenados por
valor absoluto
de menor a mayor, a continuacion, ordenados por el argumento de menor a mayor). Podemos definir una funcion inyectiva (es decir, una a una)
f
:
A
→
Q
dada por
 , donde
, donde
 es el
n
-esimo
primo
.
es el
n
-esimo
primo
.
Proposicion:
Si
A
n
es un conjunto contable para cada
n
en
N
entonces la union de todos los
A
n
es tambien contable.
[
14
]
Prueba:
Esto es una consecuencia del hecho de que para cada
n
existe una funcion subyectiva
g
n
:
N
→
A
n
y por lo tanto la funcion

dada por
G
(
n
,
m
) =
g
n
(
m
)
es una subyeccion. Ya que
N
×
N
es numerable, el corolario implica que la union es contable. Usamos el
axioma de la eleccion numerable
en esta prueba para escoger para cada
n
in
N
una subyeccion
g
n
de la coleccion no vacia de subyecciones de
N
a
A
n
.
Una prueba topologica para la incontabilidad de los numeros reales se describe en la
propiedad de la interseccion finita
.
Modelo minimo de la teoria de conjuntos
[
editar
]
Si hay un conjunto que es un modelo estandar (ver
modelo interno
) de la teoria de conjuntos de ZFC, entonces no hay un modelo estandar minimo (
ver
universo constructible
). El
teorema de Lowenheim-Skolem
se puede utilizar para demostrar que este modelo minimo es contable. El hecho es que la nocion de "incontabilidad" tiene sentido en este modelo, y en particular este modelo
M
contiene elementos que son:
- Subconjuntos de
M
, por lo tanto, contables
- Pero incontables bajo el punto de vista de
M
En los primeros dias de existencia, esta teoria fue considerada como una paradoja (vease
paradoja de Skolem
).
El modelo estandar minimo incluye a todos los
numeros algebraicos
y a todos los
numeros trascendentales
efectivamente computables, asi como a muchos otros tipos de numeros.
Ordenes totales
[
editar
]
Los conjuntos numerables pueden ser
ordenados totalmente
de diversas maneras, por ejemplo:
- Con un
buen orden
(vease tambien
numero ordinal
):
- El orden habitual de los numeros naturales (0 , 1, 2, 3, 4, 5, ...)
- Los numeros enteros en el orden (0, 1, 2, 3, ...; -1, -2, -3, ...)
- Otros (sin un buen orden):
- El orden habitual de numeros enteros (..., -3, -2, -1, 0, 1, 2, 3, ...)
- El orden habitual de los numeros racionales (no se puede escribir de forma explicita como una lista ordenada)
Notese que en ambos ejemplos del buen orden, cualquier subconjunto tiene un
elemento menor
; y en los ejemplos de las ordenaciones sin buen orden,
algunos
subconjuntos no tienen un
elemento menor
.
Esta es la definicion clave que determina si una orden total es tambien un buen orden.
Ejemplos
[
editar
]
|

|
- El conjunto de todos los numeros
pares
, es numerable porque la funcion:


es una
biyeccion
: cada numero natural corresponde a un unico numero par y viceversa.
- El conjunto
 de todos los enteros tambien es numerable.
de todos los enteros tambien es numerable.
- Ademas el conjunto
 de todos los numeros racionales es numerable.
[
15
]
de todos los numeros racionales es numerable.
[
15
]
- El conjunto
 es numerable.
es numerable.
- Se deriva del enunciado anterior que el conjunto de todos los racionales tambien es numerable, teniendo en cuenta que
 , donde
, donde
 no contiene el 0 .
no contiene el 0 .
- Por induccion puede probarse que
 son numerables para cualquier numero natural
k
.
son numerables para cualquier numero natural
k
.
Vease tambien
[
editar
]
Notas y referencias
[
editar
]
- ↑
Stillwell, John C.
(2010),
Roads to Infinity: The Mathematics of Truth and Proof
, CRC Press, p. 10,
ISBN
9781439865507
, ≪El descubrimiento de Cantor de los conjuntos numerables en 1874 fue uno de los eventos mas inesperados de la historia de las matematicas. Antes de 1874, el infinito no estaba considerado un numero matematico por la mayoria de la gente, de ahi la necesidad de distinguir entre contable e incontable.≫
.
- ↑
Cantor 1878, p. 242.
- ↑
Ferreiros 2007, pp. 268, 272-273.
- ↑
y en 1873 en su correspondencia con Dedekind.
- ↑
Cantor (1874)
Uber eine Eigenschaft des Inbegriffes aller reellen algebraischen Zahlen
, Journal de Crelle 77, p258-262 (ver el centro de numeracion de Gottingen
[1]
(
enlace roto
disponible en
Internet Archive
; vease el
historial
, la
primera version
y la
ultima
).
). Disponemos del origen de esta demostracion, que todavia no es la demostracion mas conocida que utiliza el argumento diagonal, gracias a las cartas del 7 y 9 de diciembre de 1873 de Georg Cantor a
Richard Dedekind
.
- ↑
Demostracion de Dedekind, segun su correspondencia.
- ↑
Vease por ejemplo Kneale and Kneale,
The development of Logic
Clarendon Press 1962, p 673.
- ↑
Kamke, 1950
- ↑
Halmos, 1960
- ↑
Avelsgaard, 1990
- ↑
Avelsgaard, 1990
- ↑
Halmos, 1960
- ↑
Avelsgaard, 1990
- ↑
Fletcher y Patty, 1988
- ↑
Se dispone en un cuadro cuya cada fila corresponde a fracciones que tienen el mismo numerador, luego se van uniendo, racionales de diferentes filas
Enlaces externos
[
editar
]