 Ungerichteter Graph mit sechs Knoten
Ungerichteter Graph mit sechs Knoten
Die
Graphentheorie
(seltener auch
Grafentheorie
) ist ein Teilgebiet der
diskreten Mathematik
und der
theoretischen Informatik
.
Betrachtungsgegenstand
der Graphentheorie sind
Graphen
(
Mengen
von
Knoten
und
Kanten
), deren
Eigenschaften
und ihre
Beziehungen
zueinander.
Graphen sind mathematische
Modelle
fur netzartige Strukturen in Natur und Technik (wie
soziale Strukturen
,
Straßennetze
,
Verwandtschaftsbeziehungen
,
Computernetze
,
elektrische Schaltungen
,
Versorgungsnetze
oder chemische
Molekule
). In der Graphentheorie untersucht man lediglich die abstrakte Netzstruktur an sich. Die Art, Lage und Beschaffenheit der Knoten und Kanten bleibt unberucksichtigt. Es verbleiben jedoch viele allgemeingultige
Graphen-Eigenschaften
, die bereits auf dieser Abstraktionsstufe untersucht werden konnen und sich in allgemeingultigen Aussagen (
Satze der Graphentheorie
) wiederfinden.
[1]
Ein Beispiel hierfur ist das
Handschlaglemma
, wonach die Summe der
Knotengrade
in einem Graphen stets gerade ist (in der nebenstehenden Abbildung: 14).
Dadurch, dass einerseits viele algorithmische Probleme auf Graphen zuruckgefuhrt werden konnen und andererseits die Losung
graphentheoretischer Probleme
oft auf
Algorithmen
basiert, ist die Graphentheorie auch in der
Informatik
, insbesondere der
Komplexitatstheorie
, von großer Bedeutung. Insbesondere lassen sich viele
Aufgaben
der
kombinatorischen Optimierung
in der Sprache der Graphentheorie formulieren und umgekehrt graphentheoretische Probleme als
lineare ganzzahlige Optimierungsprobleme
modellieren
.
[2]
Die Untersuchung von Graphen ist auch Inhalt der
Netzwerktheorie
. Graphen werden insbesondere durch die
Datenstrukturen
Adjazenzmatrix
,
Inzidenzmatrix
oder
Adjazenzliste
reprasentiert.
 Das
Konigsberger Bruckenproblem
im Stadtplan …
Das
Konigsberger Bruckenproblem
im Stadtplan …
 … und abstrakt als Graph (Orte durch Knoten, Brucken durch Kanten reprasentiert)
… und abstrakt als Graph (Orte durch Knoten, Brucken durch Kanten reprasentiert)
Ein von der Graphentheorie unabhangiger Vorlaufer in der
Antike
war die Methode
Dihairesis
, mit deren Hilfe man (nur teilweise grafisch) zoologische, musikwissenschaftliche und andere Begriffe hierarchisierte. Es entstanden so fruhe Systematiken innerhalb verschiedener Wissensgebiete.
Die Anfange der Graphentheorie gehen bis in das Jahr 1736 zuruck. Damals publizierte
Leonhard Euler
eine Losung fur das
Konigsberger Bruckenproblem
. Die Frage war, ob es einen Rundgang durch die Stadt
Konigsberg (Preußen)
gibt, der jede der sieben Brucken uber den Fluss
Pregel
genau einmal benutzt. Euler konnte eine fur dieses Problem nicht erfullbare notwendige Bedingung angeben und so die Existenz eines solchen Rundganges verneinen.
1852 bemerkte der Mathematiker und Botaniker
Francis Gutherie
, dass vier Farben reichen, um eine Landkarte so zu farben, dass zwei aneinander grenzende Lander stets unterschiedlich gefarbt sind. Viele Mathematiker beschaftigten sich mit diesem
Farbungsproblem
. Es dauerte jedoch bis 1976, bis der
Vier-Farben-Satz
mittels Computer bewiesen werden konnte.
[3]
Erst 1997 stellten
Neil Robertson
, Daniel Sanders,
Paul Seymour
,
Robin Thomas
einen neuen Beweis vor.
[4]
Der Begriff
Graph
wurde in Anlehnung an graphischen Notationen chemischer Strukturen erstmals 1878 von dem Mathematiker
James Joseph Sylvester
verwendet.
[5]
Als weiterer Begrunder der fruhen Graphentheorie gilt
Arthur Cayley
. Eine der ersten Anwendungen waren chemische
Konstitutionsformeln
.
[6]
[7]
(Siehe auch
Chemische Graphentheorie
und
Literatur
: Bonchev/Rouvray, 1990). Das erste Lehrbuch zur Graphentheorie erschien 1936 von
Denes K?nig
.
[8]
In der zweiten Halfte des 20. Jahrhunderts hat
William Thomas Tutte
maßgeblich an der Weiterentwicklung der Graphentheorie gearbeitet und dieses Teilgebiet der Mathematik stark gepragt.
Teilgebiete der Graphentheorie sind:
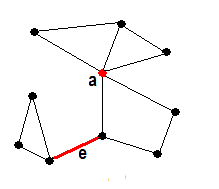 Graph mit Artikulation und Brucke
Graph mit Artikulation und Brucke
In der Graphentheorie bezeichnet ein Graph eine Menge von Knoten (auch Ecken oder Punkte genannt) zusammen mit einer Menge von Kanten. Eine Kante ist hierbei eine
Menge
von genau zwei Knoten. Sie gibt an, ob zwei
Knoten
miteinander in Beziehung stehen, bzw. ob sie in der bildlichen Darstellung des Graphen verbunden sind. Zwei Knoten, die durch eine Kante verbunden sind, heißen
benachbart
oder adjazent
.
Wenn die Kanten statt durch Mengen durch
geordnete Paare
von Knoten angegeben sind, spricht man von
gerichteten Graphen
. In diesem Falle unterscheidet man zwischen der Kante (
a
,
b
) ? als Kante von Knoten
a
zu Knoten
b
? und der Kante (
b
,
a
) ? als Kante von Knoten
b
zu Knoten
a
. Knoten und Kanten konnen auch mit Farben (formal mit
naturlichen Zahlen
) oder Gewichten (d. h.
rationalen
oder
reellen Zahlen
) versehen werden. Man spricht dann von knoten- bzw. kanten
gefarbten
oder -
gewichteten
Graphen.
Komplexere Graphentypen sind:
- Multigraphen
, bei denen die Kantenmenge eine
Multimenge
ist
- Hypergraphen
, bei denen eine Kante eine beliebig große Menge von Knoten darstellt (man spricht in diesem Falle auch von
Hyperkanten
)
- Petri-Netze
mit zwei Arten von Knoten
Ist die Menge der Knoten endlich, spricht man von
endlichen Graphen
, ansonsten von
unendlichen Graphen
.
 Zusammenhangskomponenten
Zusammenhangskomponenten
Graphen konnen verschiedene Eigenschaften haben. So kann ein Graph
Es kann nach der Existenz spezieller
Teilgraphen
oder
Minoren
gefragt werden oder bestimmte Parameter untersucht werden, wie zum Beispiel
Knotenzahl
,
Kantenzahl
,
Minimalgrad
,
Maximalgrad
,
Taillenweite
,
Durchmesser
,
Knotenzusammenhangszahl
,
Kantenzusammenhangszahl
,
Bogenzusammenhangszahl
,
chromatische Zahl
,
Knotenuberdeckungszahl
(
Faktor
),
Unabhangigkeitszahl
(
Stabilitatszahl
) oder
Cliquenzahl
. Zwei Graphen konnen
isomorph
(strukturell gleich) oder
automorph
zueinander sein.
Die verschiedenen Eigenschaften konnen zueinander in Beziehung stehen. Die Beziehungen zu untersuchen ist eine Aufgabe der Graphentheorie. Beispielsweise ist die Knotenzusammenhangszahl nie großer als die Kantenzusammenhangszahl, welche wiederum nie großer als der Minimalgrad des betrachteten Graphen ist. In
ebenen Graphen
ist die Farbungszahl immer kleiner als funf. Diese Aussage ist auch als der
Vier-Farben-Satz
bekannt.
 gerichteter zyklischer Graph
gerichteter zyklischer Graph
Einige der aufgezahlten Grapheneigenschaften sind relativ schnell algorithmisch bestimmbar, etwa wenn der Aufwand hochstens mit dem Quadrat der Große der Graphen wachst. Andere Eigenschaften praktisch angewandter Graphen sind innerhalb der Lebensdauer heutiger Computer nicht exakt zu bestimmen. Allerdings kann in diesen Fallen der Einsatz von
heuristischen Verfahren
zu sinnvollen Naherungslosungen fuhren.
 Bipartiter Graph
Bipartiter Graph
Grundsatzlich werden Graphen in
gerichtete
und
ungerichtete
Graphen unterteilt.
Aufgrund des
Zusammenhangs
unterscheidet man:
Aufgrund des Vorhandenseins bestimmter Eigenschaften lassen sich weitere Graphenklassen unterscheiden wie
Wenn ein Knoten besonders ausgezeichnet ist, spricht man von einer
Wurzel
bzw. einem
gewurzeltem Graphen
. Besondere Bedeutung haben
gewurzelte Baume
unter anderem auch als
Baumstruktur
.
Die wichtigsten Probleme und Ergebnisse der Graphentheorie werden im Folgenden dargestellt:
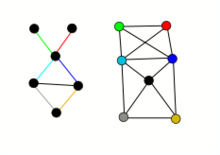 Graphfarbung
Graphfarbung
Ein bekanntes Problem fragt, wie viele Farben man braucht, um die Lander einer Landkarte einzufarben, sodass keine zwei benachbarten Lander die gleiche Farbe zugewiesen bekommen. Die Nachbarschaftsbeziehung der Lander kann man als planaren Graph reprasentieren. Das Problem kann nun als Knoten-Farbungsproblem modelliert werden. Nach dem
Vier-Farben-Satz
braucht man maximal vier verschiedene Farben. Ob sich im Allgemeinen ein Graph mit weniger Farben einfarben lasst, kann man nach heutigem Wissensstand nicht effizient entscheiden. Das Problem gilt als eines der schwierigsten Probleme in der Klasse der
NP
-vollstandigen
Probleme. Unter der Voraussetzung, dass
P
≠
NP
, ist selbst eine bis auf einen konstanten Faktor angenaherte Losung nicht effizient moglich.
Eine wichtige Anwendung der algorithmischen Graphentheorie ist die Suche nach einer kurzesten Route zwischen zwei Orten in einem Straßennetz. Dieses Problem kann man als Graphenproblem modellieren. Hierzu abstrahiert man das Straßennetz, in dem man alle Orte als Knoten aufnimmt, und eine Kante hinzufugt, wenn es eine Verbindung zwischen diesen Orten gibt. Die Kanten dieses Graphen werden je nach Anwendung
gewichtet
, zum Beispiel mit der Lange der assoziierten Verbindung. Mit Hilfe eines Algorithmus zum Finden von kurzesten Pfaden (beispielsweise mit dem
Algorithmus von Dijkstra
) kann eine kurzeste Verbindung effizient gefunden werden (siehe auch:
Kategorie:Graphsuchalgorithmen
).
 Handlungsreisendenproblem
Handlungsreisendenproblem
Algorithmisch deutlich schwieriger ist die Bestimmung einer kurzesten Rundreise (siehe
Problem des Handlungsreisenden
), bei der alle Orte eines Straßennetzes genau einmal besucht werden mussen. Da die Zahl der moglichen Rundreisen faktoriell mit der Zahl der Orte wachst, ist der naive Algorithmus, alle Rundreisen auszuprobieren und die kurzeste auszuwahlen, fur praktische Anwendungen nur fur sehr kleine Netzwerke praktikabel. Es existieren fur dieses Problem eine Reihe von
Approximationsalgorithmen
, die eine gute aber nicht eine optimale Rundreise finden. So liefert die
Christofides-Heuristik
eine Rundreise die maximal 1,5-mal so lang ist wie die bestmogliche. Unter der Annahme, dass
P
≠
NP
(
siehe
P-NP-Problem
), existiert kein effizienter Algorithmus fur die Bestimmung einer optimalen Losung, da dieses Problem
NP
-schwer
ist.
Das
Konigsberger Bruckenproblem
fragt nach der Existenz eines
Eulerkreises
. Wahrend sich das Eulerkreisproblem mittels
Hierholzer-Verfahren
in linearer Zeit losen lasst, ist das Finden eines
Hamiltonkreises
(ein geschlossener
Pfad
in einem Graphen, der jeden Knoten genau einmal enthalt) NP-schwierig. Beim
Brieftragerproblem
wird nach einem kurzesten Zyklus gefragt, der alle Kanten mindestens einmal durchlauft.
Beim Zusammenhang wird gefragt, ob bzw. uber wie viele Wege zwei Knoten untereinander
erreichbar
sind. Dies spielt beispielsweise bei der Beurteilung der Versorgungsnetze hinsichtlich der kritischen (ausfallbedrohten Teile) eine Rolle.
 Graph mit Cliquen
Graph mit Cliquen
Die Frage nach dem Vorhandensein (ggf. maximaler)
Cliquen
sucht die Teile eines Graphen, die untereinander
vollstandig
mit Kanten verbunden sind.
Das Knotenuberdeckungsproblem sucht nach einer Teilmenge von Knoten eines Graphen, die von jeder Kante mindestens einen Endknoten enthalt.
Mit der Frage nach dem maximalen Fluss lassen sich Versorgungsnetze hinsichtlich ihrer Kapazitat beurteilen.
 Matching im bipartiten Graphen
Matching im bipartiten Graphen
Matchingprobleme, die sich auf
Flussprobleme
zuruckfuhren lassen, fragen nach der optimalen Auswahl von Kanten, so dass keine zwei Kanten inzident zu einem Knoten sind. Damit lassen sich
Zuordnungsprobleme
, beispielsweise der Ressourcennutzung wie Raum- oder Maschinenbelegung losen.
Zu den weiteren Graphenproblemen zahlen
- Martin Aigner:
Graphentheorie: eine Entwicklung aus dem 4-Farben-Problem.
1984 (269 Seiten).
- Daniel Bonchev, D. H. Rouvray:
Chemical Graph Theory: Introduction and Fundamentals.
Abacus, New York NY 1990/1991,
ISBN 0-85626-454-7
.
- J. Sedlacek:
Einfuhrung in die Graphentheorie.
B. G. Teubner, Leipzig 1968, 1972.
- M. Nitzsche:
Graphen fur Einsteiger (Rund um das Haus vom Nikolaus).
Vieweg, Wiesbaden 2004,
ISBN 3-528-03215-4
.
- R. Diestel:
Graphentheorie.
3. Auflage. Springer, Heidelberg 2005,
ISBN 3-540-67656-2
(
online-download
).
- Peter Gritzmann, Rene Brandenberg:
Das Geheimnis des kurzesten Weges. Ein mathematisches Abenteuer
. 2. Auflage. Springer, Berlin/Heidelberg 2003,
ISBN 3-540-00045-3
.
- Peter Tittmann:
Graphentheorie. Eine anwendungsorientierte Einfuhrung.
3. Auflage. Hanser, Munchen 2019,
ISBN 978-3-446-46052-2
.
- ↑
Peter Tittmann:
Graphentheorie. Eine anwendungsorientierte Einfuhrung
. 3., aktualisierte Auflage. Munchen,
ISBN 978-3-446-46052-2
,
S.
1
.
- ↑
Bernhard Korte, Jens Vygen:
Combinatorial Optimization
. In:
Algorithms and Combinatorics
. 2002,
ISSN
0937-5511
,
doi
:
10.1007/978-3-662-21711-5
(
uni-muenchen.de
[PDF; abgerufen am 16. Januar 2024]).
- ↑
Peter Tittmann:
Graphentheorie. Eine anwendungsorientierte Einfuhrung
. 3., aktualisierte Auflage. Munchen,
ISBN 978-3-446-46052-2
,
S.
76
.
- ↑
Neil Robertson, Daniel Sanders, Paul Seymour, Robin Thomas:
The Four-Colour Theorem
. In:
Journal of Combinatorial Theory, Series B
.
Band
70
,
Nr.
1
, 1997,
ISSN
0095-8956
,
S.
2?44
.
- ↑
James Joseph Sylvester:
Chemistry and Algebra.
In:
Nature.
Band 17, 1878, S. 284.
- ↑
Norman L. Biggs, E. Keith Lloyd, Robin J. Wilson:
Graph Theory 1736?1936
. Oxford University Press, 1999,
ISBN 0-19-853916-9
.
- ↑
Arthur Cayley:
Chemical Graphs
. In:
Philosophical Magazine
. Band 47, 1874, S. 444?446.
- ↑
Denes K?nig:
Theorie der Endlichen und Unendlichen Graphen: Kombinatorische Topologie der Streckenkomplexe.
Akademische Verlagsgesellschaft, Leipzig 1936.