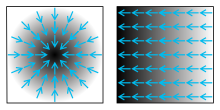
 Zwei Skalarfelder, dargestellt als Grauschattierung (dunklere Farbung entspricht großerem Funktionswert). Die blauen Pfeile darauf symbolisieren den zugehorigen Gradienten.
Zwei Skalarfelder, dargestellt als Grauschattierung (dunklere Farbung entspricht großerem Funktionswert). Die blauen Pfeile darauf symbolisieren den zugehorigen Gradienten.
Der
Gradient
als
Operator
der
Mathematik
verallgemeinert die bekannten
Gradienten
(meist aus der Physik), die den Verlauf von physikalischen Großen beschreiben. Als
Differentialoperator
kann er beispielsweise auf ein
Skalarfeld
angewandt werden und wird in diesem Fall ein
Vektorfeld
liefern, das
Gradientenfeld
genannt wird. Der Gradient ist eine Verallgemeinerung der
Ableitung
in der
mehrdimensionalen Analysis
. Zur besseren Abgrenzung zwischen Operator und Resultat seiner Anwendung bezeichnet man solche Gradienten skalarer Feldgroßen in manchen Quellen auch als Gradientvektoren.
[1]
In
kartesischen Koordinaten
sind die Komponenten des Gradientvektors die
partiellen Ableitungen
im Punkt
 , der Gradient zeigt deshalb in die Richtung des großten Wertanstiegs. Der Betrag des Gradienten gibt den Wert der großten Anderungsrate an diesem Punkt an.
, der Gradient zeigt deshalb in die Richtung des großten Wertanstiegs. Der Betrag des Gradienten gibt den Wert der großten Anderungsrate an diesem Punkt an.
Beispielsweise kann man die
Reliefkarte
einer Landschaft so auffassen, dass sie jedem Ort
 die Hohe
die Hohe
 an dieser Stelle zuordnet. Dann ist der Gradient an der Stelle
an dieser Stelle zuordnet. Dann ist der Gradient an der Stelle
 genau der Vektor (?Pfeil“), der in die
Richtung
des großten Hohenanstiegs bei
genau der Vektor (?Pfeil“), der in die
Richtung
des großten Hohenanstiegs bei
 zeigt. Der
Betrag
(?Lange“) dieses Vektors gibt an, wie stark die (großte)
Steigung
an diesem Punkt ist.
zeigt. Der
Betrag
(?Lange“) dieses Vektors gibt an, wie stark die (großte)
Steigung
an diesem Punkt ist.
Zu jeder Stelle
 gibt es genau einen Gradienten. Zeichnet man zu allen Stellen
gibt es genau einen Gradienten. Zeichnet man zu allen Stellen
 der Reliefkarte den jeweils zugehorigen Gradientenvektor ein, dann erhalt man das gesamte
Vektorfeld
.
der Reliefkarte den jeweils zugehorigen Gradientenvektor ein, dann erhalt man das gesamte
Vektorfeld
.
Der Gradient wird zusammen mit anderen Differentialoperatoren wie
Divergenz
und
Rotation
in der
Vektor-
und
Tensoranalysis
, Teilgebieten der
mehrdimensionalen Analysis
, untersucht. Sie werden mit dem gleichen Vektoroperator gebildet, und zwar mit dem
Nabla-Operator
 (bisweilen auch
(bisweilen auch
 oder
oder
 um anzudeuten, dass der Nabla-Operator hilfsweise als Vektor verstanden werden kann).
um anzudeuten, dass der Nabla-Operator hilfsweise als Vektor verstanden werden kann).
Auf
 sei das
Skalarprodukt
sei das
Skalarprodukt
 gegeben. Der Gradient
gegeben. Der Gradient
 der total differenzierbaren Funktion
der total differenzierbaren Funktion
 im Punkt
im Punkt
 ist der durch die Forderung
ist der durch die Forderung

eindeutig bestimmte Vektor
 Der Operator
Der Operator
 ist das
totale Differential
bzw. die
Cartan-Ableitung
.
ist das
totale Differential
bzw. die
Cartan-Ableitung
.
Der Gradient hat fur
differenzierbare
Funktionen
 die definierende Eigenschaft
[2]
die definierende Eigenschaft
[2]
![{\displaystyle f({\vec {y}})-f({\vec {a}})=\mathrm {grad} f({\vec {a}})[{\vec {y}}-{\vec {a}}]+{\mathcal {O}}(|{\vec {y}}-{\vec {a}}|)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30f191d47d7f6e362c9c9d472888796b970a1d30) fur
fur

Das
Landau-Symbol
 steht fur Terme, die langsamer als
steht fur Terme, die langsamer als
 wachsen, und
wachsen, und
![{\displaystyle \ldots [{\vec {h}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04ca99ddbb4750a35cee3d794c2f93d1c75d4501) stellt eine lineare Funktion von
stellt eine lineare Funktion von
 dar. Wenn der Gradient existiert, ist er eindeutig und kann aus
dar. Wenn der Gradient existiert, ist er eindeutig und kann aus
![{\displaystyle \mathrm {grad} f({\vec {a}})[{\vec {h}}]=\left.{\frac {\mathrm {d} }{\mathrm {d} s}}f({\vec {a}}+s{\vec {h}})\right|_{s=0}=\lim _{s\to 0}{\frac {f({\vec {a}}+s{\vec {h}})-f({\vec {a}})}{s}}=({\vec {h}}\cdot \nabla )f}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2652706894e56c5f17a4fea9ebd271ea00dd614b)
berechnet werden, wo
 der
Nabla-Operator
ist. So werden auch Gradienten fur Skalar-, Vektor- und Tensorfelder zweiter Stufe oder allgemein Tensorfelder n-ter Stufe definiert.
[3]
der
Nabla-Operator
ist. So werden auch Gradienten fur Skalar-, Vektor- und Tensorfelder zweiter Stufe oder allgemein Tensorfelder n-ter Stufe definiert.
[3]
Fur ein Skalarfeld folgt hieraus
 ; oft schreibt man daher
; oft schreibt man daher
 (gesprochen ?
Nabla
(gesprochen ?
Nabla
 “) statt
“) statt
 .
.
Der Gradient hat in unterschiedlichen Koordinatensystemen auch unterschiedliche Darstellungen.
Im
 mit dem euklidischen
Standardskalarprodukt
ist
mit dem euklidischen
Standardskalarprodukt
ist
 der Spaltenvektor
der Spaltenvektor

Die Eintrage
 sind die
partiellen Ableitungen
von
sind die
partiellen Ableitungen
von
 in
in
 -Richtung.
-Richtung.
Gegeben sei ein Skalarfeld durch
 in der
xy-Ebene
. Es hat die partiellen Ableitungen
in der
xy-Ebene
. Es hat die partiellen Ableitungen
 und
und
 und es folgt
und es folgt
 oder in Vektordarstellung
oder in Vektordarstellung

Fur den Punkt
 lautet beispielsweise der Gradientvektor
lautet beispielsweise der Gradientvektor
 . Der Betrag ist
. Der Betrag ist
 .
.
- Darstellung in dreidimensionalen
Zylinderkoordinaten
:


- Darstellung in dreidimensionalen
Kugelkoordinaten
:


Dies sind Spezialfalle des Gradienten auf
riemannschen Mannigfaltigkeiten
. Fur diese Verallgemeinerung siehe:
Außere Ableitung
.
In allgemeinen
orthogonalen Koordinaten
hat der Gradient die Darstellung

wobei die
 den Betrag und
den Betrag und
 die Richtung des Vektors
die Richtung des Vektors
 angeben.
angeben.
In
allgemein krummlinigen Koordinaten
hat der Gradient die Darstellung

worin
 der Gradient der Koordinate
der Gradient der Koordinate
 ist.
ist.
Eine anschauliche Bedeutung hat der Gradient im schon eingangs erwahnten Fall von (zweidimensionalen) Landkarten, in denen Hohenangaben eingetragen sind.
[4]
Die Hohenfunktion ist dann ein Skalarfeld, das jedem Punkt auf der Landkarte (gekennzeichnet durch eine x- und eine y-Koordinate) eine Hohe zuordnet. Der Gradient dieses Skalarfelds in einem Punkt ist ein Vektor, der in Richtung des steilsten Anstiegs der Hohenfunktion weist, und der Betrag des Gradienten entspricht der Starke dieses Anstiegs. Der Gradient steht dabei in jedem Punkt senkrecht auf der
Hohenlinie
(
Niveaumenge
) der Hohenfunktion durch diesen Punkt. In einem lokalen Minimum oder Maximum (
Extremum
) oder an einem
Sattelpunkt
ist der Gradient gerade der
Nullvektor
, vorausgesetzt, dass dieser Extrempunkt im Inneren des betrachteten Gebietes liegt.
Mit Hilfe des Gradienten lasst sich auch der Anstieg in jeder beliebigen Richtung ermitteln. Diese sogenannte
Richtungsableitung
ist ? im Unterschied zum Gradienten ? ein Skalar. Lauft man im Gebiet in (infinitesimal) kleinen Trippelschritten von einem Punkt a zum Punkt b und summiert das Produkt aus Schrittlange und Richtungsableitung in Richtung des Schritts, erhalt man im Zielpunkt b als Ergebnis die Hohendifferenz zum Startpunkt a. Diese Hohendifferenz ist offensichtlich wegunabhangig. Fallen insbesondere Start- und Endpunkt zusammen, so hat man am Ende seine Hohe nicht verandert, egal welchen Weg man durch das Gebiet eingeschlagen hat.
Mit Hilfe des
Integralsatzes von Gauß
kann der Gradient, ahnlich wie die
Divergenz
(Quellendichte) und die
Rotation
(Wirbeldichte) als
Volumenableitung
dargestellt werden. Diese Darstellung hat den Vorteil, dass sie koordinatenunabhangig ist. Aus diesem Grund wird der Gradient im Bereich der
Ingenieurwissenschaften
oftmals direkt so definiert.
Ist
 ein Raumgebiet mit stuckweise glattem Rand
ein Raumgebiet mit stuckweise glattem Rand
 und dem Volumen
und dem Volumen
 dann kann der Gradient des Skalarfelds
dann kann der Gradient des Skalarfelds
 im Punkt
im Punkt
 mittels der Volumenableitung durch
mittels der Volumenableitung durch

berechnet werden. Dabei bezeichnet
 das
außere vektorielle Flachenelement
von
das
außere vektorielle Flachenelement
von
 wobei
wobei
 der nach außen zeigende
Normalenvektor
und
der nach außen zeigende
Normalenvektor
und
 das skalare Flachenelement ist.
[5]
das skalare Flachenelement ist.
[5]
Zur Grenzwertbildung wird das Raumgebiet
 auf den Punkt
auf den Punkt
 zusammengezogen, sodass sein Inhalt
zusammengezogen, sodass sein Inhalt
 im
Volumenintegral unten
gegen null geht. Ersetzt man
im
Volumenintegral unten
gegen null geht. Ersetzt man
 durch einen
Druck
, erscheint der Gradient als
Kraftdichte
. Die Koordinatendarstellungen ergeben sich aus der
Volumenableitung
, wenn man das jeweilige Volumenelement, beispielsweise Kugel oder Zylinder, als Raumgebiet
durch einen
Druck
, erscheint der Gradient als
Kraftdichte
. Die Koordinatendarstellungen ergeben sich aus der
Volumenableitung
, wenn man das jeweilige Volumenelement, beispielsweise Kugel oder Zylinder, als Raumgebiet
 wahlt.
wahlt.
Fur alle Konstanten
 und Skalarfelder
und Skalarfelder
 gilt:
gilt:

- Linearitat


- Produktregel

- Kettenregel


- Siehe auch
#Nutzliche Formeln
.
- Integralsatze

- Dabei ist ?·“ das
Skalarprodukt
und der Weg von
 nach
nach
 beliebig. Diese Wegunabhangigkeit zeichnet Gradientenfelder aus
[6]
, siehe auch
#Konservative Krafte
.
beliebig. Diese Wegunabhangigkeit zeichnet Gradientenfelder aus
[6]
, siehe auch
#Konservative Krafte
.


- Hier ist ?ד das
Kreuzprodukt
,
 ein zweimal
stetig differenzierbares
Feld und
ein zweimal
stetig differenzierbares
Feld und
 der nach außen gerichtete
Normaleneinheitsvektor
auf der geschlossenen Oberflache
der nach außen gerichtete
Normaleneinheitsvektor
auf der geschlossenen Oberflache
 des Volumens
des Volumens
 [7]
und
[7]
und
 die stuckweise glatte, geschlossene Berandungskurve der Flache
die stuckweise glatte, geschlossene Berandungskurve der Flache
 .
[6]
Aus dem ersten Volumenintegral folgt die Koordinatenfreie Darstellung als Volumenableitung, wenn das Volumen so klein wird, dass in ihm der Gradient naherungsweise konstant ist.
.
[6]
Aus dem ersten Volumenintegral folgt die Koordinatenfreie Darstellung als Volumenableitung, wenn das Volumen so klein wird, dass in ihm der Gradient naherungsweise konstant ist.
Unter der Richtungsableitung versteht man die
Ableitung
, also den Anstieg eines
Skalarfeldes
 in Richtung eines normierten Vektors
in Richtung eines normierten Vektors
 genauer:
genauer:

Ist
 in einer Umgebung von
in einer Umgebung von
 differenzierbar, dann kann man die Richtungsableitung als
Skalarprodukt
von
differenzierbar, dann kann man die Richtungsableitung als
Skalarprodukt
von
 mit dem Gradienten von
mit dem Gradienten von
 berechnen:
berechnen:

Letztere Form ist nicht auf Skalarfelder beschrankt und auf Vektor- oder Tensorfelder n-ter Stufe anwendbar und wird insbesondere in der
Stromungsmechanik
vielfaltig angewendet.
Eine wichtige Beziehung fur differenzierbare Gradientenfelder
 in
in
 Dimensionen ist die Aussage, dass diese (nach dem
Satz von Schwarz
) immer ?integrabel“ sind, und zwar in folgendem Sinne: Es gilt fur alle
Dimensionen ist die Aussage, dass diese (nach dem
Satz von Schwarz
) immer ?integrabel“ sind, und zwar in folgendem Sinne: Es gilt fur alle
 und
und

 :
:

Diese direkt nachprufbare Beziehung ? in drei Dimensionen identisch mit der
Rotations
freiheit des Feldes ? ist notwendig fur die Existenz einer ?Potentialfunktion“
 (praziser: der Funktion
(praziser: der Funktion
 ). Die
). Die
 bzw.
bzw.
 sind die Komponenten des Vektorfeldes. Die Integrabilitatsbedingung impliziert ferner, dass fur
alle
geschlossenen Wege
sind die Komponenten des Vektorfeldes. Die Integrabilitatsbedingung impliziert ferner, dass fur
alle
geschlossenen Wege
 im
im
 das Linienintegral
das Linienintegral
 verschwindet, was in der Mechanik bzw. der Elektrodynamik große Bedeutung hat.
verschwindet, was in der Mechanik bzw. der Elektrodynamik große Bedeutung hat.
Lokal gilt auch das Umgekehrte: Die Integrabilitatsbedingung

fur ein differenzierbares Vektorfeld
 ist auch hinreichend fur die lokale Existenz einer skalaren Potentialfunktion
ist auch hinreichend fur die lokale Existenz einer skalaren Potentialfunktion
 mit
mit
 (vgl.
Totales Differential#Integrabilitatsbedingung
). Unter geeigneten Voraussetzungen an den Definitionsbereich von
(vgl.
Totales Differential#Integrabilitatsbedingung
). Unter geeigneten Voraussetzungen an den Definitionsbereich von
 (z. B.
Sternformigkeit
) kann sogar auf die globale Existenz einer solchen Potentialfunktion geschlossen werden (siehe
Poincare-Lemma
).
(z. B.
Sternformigkeit
) kann sogar auf die globale Existenz einer solchen Potentialfunktion geschlossen werden (siehe
Poincare-Lemma
).
Folgende Gradienten treten haufig in der Physik auf. Es wird der
Ortsvektor
 verwendet.
verwendet.




Im letzten Beispiel wirkt der Gradient nur auf
 und nicht auf
und nicht auf
 und wird deshalb auch als
und wird deshalb auch als
 geschrieben.
geschrieben.
In der
Physik
lassen sich viele Kraftfelder als der Gradient eines
Potentials
darstellen. Beispiele dafur sind:

- die fur eine am Koordinatenursprung befindliche zentrale Masse
M

- lautet, oder
- statische elektrische Felder
 in der
Elektrodynamik
in der
Elektrodynamik

In konservativen Kraftfeldern wird unter anderem ausgenutzt, dass fur Probemassen bzw. Probeladungen die Wegintegrale die Arbeit
 entlang eines beliebigen Weges
entlang eines beliebigen Weges
 durch das Kraftfeld nur vom Anfangs- und Endpunkt des Weges, nicht aber von seinem Verlauf abhangt, siehe
#Integralsatze
.
durch das Kraftfeld nur vom Anfangs- und Endpunkt des Weges, nicht aber von seinem Verlauf abhangt, siehe
#Integralsatze
.
Zahlreiche Transportphanomene lassen sich darauf zuruckfuhren, dass sich die dazugehorigen
Strome
als Gradient eines Skalarfeldes ausdrucken lassen, wobei der dabei auftretende Proportionalitatsfaktor als
Transportkoeffizient
oder Leitfahigkeit bezeichnet wird.
Ein Beispiel dafur ist der Warmestrom
 in der
Thermodynamik
, fur den
in der
Thermodynamik
, fur den

gilt, wobei
 die
Warmeleitfahigkeit
ist.
die
Warmeleitfahigkeit
ist.
In der
Fluidmechanik
versteht man unter einer
Potentialstromung
eine Stromung, bei der die Geschwindigkeit Gradient eines Potentialfeldes ist, siehe
Geschwindigkeitspotential
.
Ein Problem in der
Bildverarbeitung
ist es, in einem Bild zusammenhangende Flachen zu erkennen. Da ein Bild diskrete Werte enthalt, benutzt man Filter wie den
Sobel-Operator
, um ein Gradientenfeld des Bildes zu erhalten. Ein Filter ist dabei eine Matrix, mit der das Bild gefaltet wird (siehe
Diskrete Faltung
). Die Kanten in dem Bild sind dann als Extremwerte des gefilterten Bildes erkennbar.
Wie im Abschnitt
#Definition
schon bemerkt, wird der Gradient auch auf Vektoren und Tensoren angewendet. Der Gradient eines
Skalarfeldes
(Tensorfeld nullter Stufe) ergibt ein Vektorfeld, das ein Tensorfeld erster Stufe ist. Allgemein fuhrt Gradientenbildung eines Tensorfeldes n-ter Stufe auf ein Tensorfeld der Stufe n+1.
[8]
Die Koeffizienten der Gradienten der kovarianten Basisvektoren eines
krummlinigen Koordinatensystems
sind die
Christoffelsymbole
.
[9]
Insbesondere in der
Kontinuumsmechanik
und
Fluidmechanik
werden die Gradienten von Skalar- und Vektorfeldern vielfaltig genutzt, denn die oben genannten
#Eigenschaften
lassen sich ohne Weiteres auf Gradienten von Vektorfeldern ubertragen.
Fur eine
glatte Funktion
 auf einer
Riemannschen Mannigfaltigkeit
auf einer
Riemannschen Mannigfaltigkeit
 ist der Gradient von
ist der Gradient von
 dasjenige
Vektorfeld
dasjenige
Vektorfeld
 , mit dem fur jedes Vektorfeld
, mit dem fur jedes Vektorfeld
 die Gleichung
die Gleichung

gilt, wobei
 das durch
das durch
 definierte
innere Produkt
von
Tangentialvektoren
an
definierte
innere Produkt
von
Tangentialvektoren
an
 ist und
ist und
 (oft auch
(oft auch
 bezeichnet) diejenige Funktion ist, die jedem Punkt
bezeichnet) diejenige Funktion ist, die jedem Punkt
 die
Richtungsableitung
von
die
Richtungsableitung
von
 in Richtung
in Richtung
 , ausgewertet in
, ausgewertet in
 , zuordnet. Mit anderen Worten, in einer
Karte
, zuordnet. Mit anderen Worten, in einer
Karte
 von einer offenen Teilmenge von
von einer offenen Teilmenge von
 auf eine offene Teilmenge von
auf eine offene Teilmenge von
 ist
ist
 gegeben durch:
gegeben durch:

wobei
 die
die
 -te Komponente von
-te Komponente von
 in diesen Koordinaten bedeutet.
in diesen Koordinaten bedeutet.
In lokalen Koordinaten hat der Gradient also die Form

Analog zum Fall
 hat man den Zusammenhang des Gradienten mit der
außeren Ableitung
vermittels
hat man den Zusammenhang des Gradienten mit der
außeren Ableitung
vermittels

Der Ausdruck
 ist also das der 1-Form
ist also das der 1-Form
 unter dem mittels der Metrik
unter dem mittels der Metrik
 definierten
musikalischen Isomorphismus
(?sharp“)
definierten
musikalischen Isomorphismus
(?sharp“)

entsprechende Vektorfeld. Der Zusammenhang zwischen außerer Ableitung und Gradienten fur Funktionen auf dem
 ist der Spezialfall fur die durch das euklidische Skalarprodukt gegebene flache Metrik.
ist der Spezialfall fur die durch das euklidische Skalarprodukt gegebene flache Metrik.
- ↑
Ernst Grimsehl
:
Lehrbuch der Physik.
Band 1:
Mechanik, Warmelehre, Akustik.
15. Auflage, herausgegeben von Walter Schallreuter. Teubner, Leipzig 1954, S. 579.
- ↑
M. E. Gurtin:
The Linear Theory of Elasticity
. In: S. Flugge (Hrsg.):
Handbuch der Physik
. Band VI2/a, Bandherausgeber C. Truesdell. Springer, 1972,
ISBN 3-540-05535-5
,
S.
10
.
- ↑
C. B. Lang, N. Pucker:
Mathematische Methoden in der Physik
. Springer Spektrum, Berlin, Heidelberg 2016,
ISBN 978-3-662-49312-0
,
S.
420
,
doi
:
10.1007/978-3-662-49313-7
.
,
Holm Altenbach
:
Kontinuumsmechanik
. Einfuhrung in die materialunabhangigen und materialabhangigen Gleichungen. Springer-Verlag, Berlin, Heidelberg 2012,
ISBN 978-3-642-24118-5
,
S.
43
,
doi
:
10.1007/978-3-642-24119-2
.
- ↑
Guido Walz (Hrsg.):
Lexikon der Mathematik
. 2. Auflage.
Band
2
(Eig bis Inn). Springer Spektrum Verlag, Mannheim 2017,
ISBN 978-3-662-53503-5
,
S.
216
,
doi
:
10.1007/978-3-662-53504-2
.
- ↑
Bronstein, Semendjajew, Musiol, Muhlig:
Taschenbuch der Mathematik
, Verlag Harri Deutsch, Frankfurt, 8. Aufl. 2012,
Abschn. 13.2, Raumliche Differentialoperatoren
- ↑
a
b
Werner (2019), S. 433.
- ↑
Altenbach (2012), S. 45.
- ↑
C. B. Lang, N. Pucker:
Mathematische Methoden in der Physik
. Springer Spektrum, Berlin, Heidelberg 2016,
ISBN 978-3-662-49312-0
,
S.
420
f
.,
doi
:
10.1007/978-3-662-49313-7
.
und Altenbach (2012), S. 43.
- ↑
Werner (2019), S. 313.
- Adolf J. Schwab
:
Begriffswelt der Feldtheorie
. praxisnahe, anschauliche Einfuhrung; elektromagnetische Felder, Maxwellsche Gleichungen, Gradient, Rotation, Divergenz. 6., unveranderte Auflage. Springer Verlag, Berlin, Heidelberg 2002,
ISBN 3-540-42018-5
,
doi
:
10.1007/978-3-642-56339-3
.
- Konrad Konigsberger
:
Analysis
. 4. uberarbeitete Auflage.
Band
2
. Springer Verlag, Berlin, Heidelberg 2000,
ISBN 3-540-43580-8
,
doi
:
10.1007/978-3-662-05699-8
.
- Wolfgang Werner:
Vektoren und Tensoren als universelle Sprache in Physik und Technik
. Tensoralgebra und Tensoranalysis.
Band
1
. Springer Vieweg Verlag, Wiesbaden 2019,
ISBN 978-3-658-25271-7
,
doi
:
10.1007/978-3-658-25272-4
.