Der Algorithmus von Prim dient der Berechnung eines minimalen Spannbaumes in einem zusammenhangenden , ungerichteten , kantengewichteten Graphen .

Der Algorithmus wurde 1930 vom tschechischen Mathematiker Vojt?ch Jarnik entwickelt. 1957 wurde er zunachst von Robert C. Prim und dann 1959 von Edsger W. Dijkstra wiederentdeckt. Daher wird der Algorithmus in der Literatur auch gelegentlich unter anderen Namen gefuhrt, so etwa Prim-Dijkstra-Algorithmus oder Algorithmus von Jarnik, Prim und Dijkstra , im englischen Sprachraum auch Jarnik’s algorithm oder DJP algorithm .

Beschreibung [ Bearbeiten | Quelltext bearbeiten ]

Der Algorithmus beginnt mit einem trivialen Graphen ${\displaystyle T}$, der aus einem beliebigen Knoten des gegebenen Graphen besteht. In jedem Schritt wird nun eine Kante mit minimalem Gewicht gesucht, die einen weiteren Knoten mit ${\displaystyle T}$ verbindet. Diese und der entsprechende Knoten werden zu ${\displaystyle T}$ hinzugefugt. Das Ganze wird solange wiederholt, bis alle Knoten in ${\displaystyle T}$ vorhanden sind; dann ist ${\displaystyle T}$ ein minimaler Spannbaum:

• Wahle einen beliebigen Knoten als Startgraph ${\displaystyle T}$.
• Solange ${\displaystyle T}$ noch nicht alle Knoten enthalt:
  • Wahle eine Kante ${\displaystyle e}$ mit minimalem Gewicht aus, die einen noch nicht in ${\displaystyle T}$ enthaltenen Knoten ${\displaystyle v}$ mit ${\displaystyle T}$ verbindet.
  • Fuge ${\displaystyle e}$ und ${\displaystyle v}$ dem Graphen ${\displaystyle T}$ hinzu.

Der skizzierte Algorithmus wird durch folgenden Pseudocode beschrieben:

G: Graph
V
G
: Knotenmenge von G
w: Gewichtsfunktion fur Kantenlange
r: Startknoten (r ∈ V
G
)
Q: Prioritatswarteschlange
π[u]: Elternknoten von Knoten u im Spannbaum
Adj[u]: Adjazenzliste von u (alle Nachbarknoten)
wert[u]: Abstand von u zum entstehenden Spannbaum

algorithmus_von_prim
(G,w,r)
01  Q 
${\displaystyle \leftarrow }$ V
G
   //Initialisierung

02  
fur alle
 u ∈ Q
03      wert[u] 
${\displaystyle \leftarrow }$ ∞
04      π[u] 
${\displaystyle \leftarrow }$ 0
05  wert[r] 
${\displaystyle \leftarrow }$ 0
06  
solange
 Q ≠ 
${\displaystyle \varnothing }$
07      u 
${\displaystyle \leftarrow }$ extract_min
(Q)
08      
fur alle
 v ∈ Adj[u]
09          
wenn
 v ∈ Q und w(u,v) < wert[v]
10              
dann
 π[v] 
${\displaystyle \leftarrow }$ u
11                  wert[v] 
${\displaystyle \leftarrow }$ w(u,v)

Nachdem der Algorithmus endet, ergibt sich der minimale Spannbaum wie folgt:

${\displaystyle T=\left(V_{G},\lbrace \left(u,\pi [u]\right)|u\in V_{G}\backslash \lbrace r\rbrace \rbrace \right)}$

Zum Finden der leichtesten Schnittkante kann eine Prioritatswarteschlange verwendet werden. Dabei werden vom Algorithmus insgesamt ${\displaystyle |V|}$ extractMin-Operationen und ${\displaystyle |E|}$ decreaseKey-Operationen ausgefuhrt. Mit einem Fibonacci-Heap (extractMin in amortisiert ${\displaystyle O(\log |V|)}$ und decreaseKey in amortisiert ${\displaystyle O(1)}$) als Datenstruktur ergibt sich eine Gesamtlaufzeit von ${\displaystyle O(|E|+|V|\cdot \log |V|)}$.

Die Schleife ist inharent sequentiell, da sich die leichteste Kante im Schnitt von ${\displaystyle S}$ und ${\displaystyle V\setminus S}$ mit dem Hinzufugen eines neuen Knotens zu ${\displaystyle S}$ andern kann. Es ist jedoch fur die Korrektheit wichtig, dass immer die aktuell leichteste Kante ausgewahlt wird.

Auf einer Parallel Random Access Machine mit insgesamt ${\displaystyle O(|V|)}$ Prozessoren lasst sich der Zugriff auf die Prioritatswarteschlange zu konstanter Zeit beschleunigen ^[1] , sodass sich eine Gesamtlaufzeit in ${\displaystyle O(|E|+|V|)}$ ergibt. Insgesamt bieten der Algorithmus von Kruskal und der Algorithmus von Bor?vka bessere Parallelisierungsansatze.

Beispiel [ Bearbeiten | Quelltext bearbeiten ]

In diesem Beispiel wird der Ablauf des Algorithmus von Prim an einem einfachen Graphen gezeigt. Der aktuelle Baum ${\displaystyle T}$ ist jeweils grun hervorgehoben. Alle Knoten , die im jeweiligen Schritt uber eine einzelne Kante mit dem Graphen verbunden werden konnen, sind zusammen mit der jeweiligen Kante geringsten Gewichts blau hervorgehoben. Der Knoten und die Kante, die hinzugefugt werden, sind hellblau markiert.

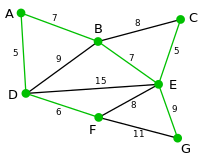
	Dies ist der Graph, zu dem der Algorithmus von Prim einen minimalen Spannbaum berechnet. Die Zahlen bei den einzelnen Kanten geben das jeweilige Kantengewicht an.
	Als Startknoten fur den Graphen ${\displaystyle T}$ wird der Knoten ${\displaystyle D}$ gewahlt. (Es konnte auch jeder andere Knoten ausgewahlt werden.) Mit dem Startknoten konnen die Knoten ${\displaystyle A}$, ${\displaystyle B}$, ${\displaystyle E}$ und ${\displaystyle F}$ jeweils unmittelbar durch die Kanten ${\displaystyle DA}$, ${\displaystyle DB}$, ${\displaystyle DE}$ und ${\displaystyle DF}$ verbunden werden. Unter diesen Kanten ist ${\displaystyle DA}$ diejenige mit dem geringsten Gewicht und wird deshalb zusammen mit dem Knoten ${\displaystyle A}$ zum Graphen ${\displaystyle T}$ hinzugefugt.
	Mit dem bestehenden Graphen ${\displaystyle T}$ kann der Knoten ${\displaystyle B}$ durch die Kanten ${\displaystyle AB}$ oder ${\displaystyle DB}$, der Knoten ${\displaystyle E}$ durch die Kante ${\displaystyle DE}$ und der Knoten ${\displaystyle F}$ durch die Kante ${\displaystyle DF}$ verbunden werden. Unter diesen vier Kanten ist ${\displaystyle DF}$ diejenige mit dem geringsten Gewicht und wird deshalb zusammen mit dem Knoten ${\displaystyle F}$ zum Graphen ${\displaystyle T}$ hinzugefugt.
	Mit dem bestehenden Graphen ${\displaystyle T}$ kann der Knoten ${\displaystyle B}$ durch die Kanten ${\displaystyle AB}$ oder ${\displaystyle DB}$, der Knoten ${\displaystyle E}$ durch die Kanten ${\displaystyle DE}$ oder ${\displaystyle FE}$ und der Knoten ${\displaystyle G}$ durch die Kante ${\displaystyle FG}$ verbunden werden. Unter diesen Kanten ist ${\displaystyle AB}$ diejenige mit dem geringsten Gewicht und wird deshalb zusammen mit dem Knoten ${\displaystyle B}$ zum Graphen ${\displaystyle T}$ hinzugefugt.
	Mit dem bestehenden Graphen ${\displaystyle T}$ kann der Knoten ${\displaystyle C}$ durch die Kante ${\displaystyle BC}$, der Knoten ${\displaystyle E}$ durch die Kanten ${\displaystyle BE}$, ${\displaystyle DE}$ oder ${\displaystyle FE}$ und der Knoten ${\displaystyle G}$ durch die Kante ${\displaystyle FG}$ verbunden werden. Unter diesen Kanten ist ${\displaystyle BE}$ diejenige mit dem geringsten Gewicht und wird deshalb zusammen mit dem Knoten ${\displaystyle E}$ zum Graphen ${\displaystyle T}$ hinzugefugt.
	Mit dem bestehenden Graphen ${\displaystyle T}$ kann der Knoten ${\displaystyle C}$ durch die Kanten ${\displaystyle BC}$ oder ${\displaystyle EC}$ und der Knoten ${\displaystyle G}$ durch die Kanten ${\displaystyle EG}$ oder ${\displaystyle FG}$ verbunden werden. Unter diesen Kanten ist ${\displaystyle EC}$ diejenige mit dem geringsten Gewicht und wird deshalb zusammen mit dem Knoten ${\displaystyle C}$ zum Graphen ${\displaystyle T}$ hinzugefugt.
	Der verbliebene Knoten ${\displaystyle G}$ kann durch die Kanten ${\displaystyle EG}$ oder ${\displaystyle FG}$ mit dem Graphen ${\displaystyle T}$ verbunden werden. Da ${\displaystyle EG}$ unter diesen beiden das geringere Gewicht hat, wird sie zusammen mit dem Knoten ${\displaystyle G}$ zum Graphen ${\displaystyle T}$ hinzugefugt.
	Der Graph ${\displaystyle T}$ enthalt jetzt alle Knoten des Ausgangsgraphen und ist ein minimaler Spannbaum dieses Ausgangsgraphen.

Effizienz und Laufzeit [ Bearbeiten | Quelltext bearbeiten ]

Fur eine effiziente Implementierung des Algorithmus von Prim muss man moglichst einfach eine Kante finden, die man dem entstehenden Baum ${\displaystyle T}$ hinzufugen kann. Man benotigt also eine Prioritatswarteschlange , in der alle Knoten gespeichert sind, die noch nicht zu ${\displaystyle T}$ gehoren. Alle Knoten haben einen Wert, der dem der leichtesten Kante entspricht, durch die der Knoten mit ${\displaystyle T}$ verbunden werden kann. Existiert keine solche Kante, wird dem Knoten der Wert ${\displaystyle \infty }$ zugewiesen. Die Warteschlange liefert nun immer einen Knoten mit dem kleinsten Wert zuruck.

Die Effizienz des Algorithmus hangt infolgedessen von der Implementierung der Warteschlange ab. Bei Verwendung eines Fibonacci-Heaps ergibt sich eine optimale Laufzeit von ${\displaystyle {\mathcal {O}}(|E|+|V|\log |V|)}$.

Korrektheitsbeweis [ Bearbeiten | Quelltext bearbeiten ]

Sei ${\displaystyle G}$ ein zusammenhangender , kantengewichteter Graph . Bei jeder Iteration des Algorithmus muss eine Kante gefunden werden, die einen Knoten in einem Teilgraphen mit einem Knoten außerhalb des Teilgraphen verbindet. Weil ${\displaystyle G}$ zusammenhangend ist, gibt es immer einen Pfad zu jedem Knoten. Der resultierende Graph ${\displaystyle T}$ des Algorithmus ist ein Baum , da die dem Baum hinzugefugte Kante und der Knoten verbunden sind.

Sei ${\displaystyle T_{1}}$ ein minimaler Spannbaum des Graphen ${\displaystyle G}$. Wenn ${\displaystyle T_{1}}$ gleich ${\displaystyle T}$ ist, dann ist ${\displaystyle T}$ ein minimaler Spannbaum.

Andernfalls sei ${\displaystyle e}$ die erste Kante, die wahrend der Konstruktion des Baums ${\displaystyle T}$ hinzugefugt wird, die sich nicht im Baum ${\displaystyle T_{1}}$ befindet, und ${\displaystyle V}$ sei die Menge der Knoten, die durch die vor der Kante ${\displaystyle e}$ hinzugefugten Kanten verbunden waren. Dann befindet sich ein Knoten der Kante ${\displaystyle e}$ in der Menge ${\displaystyle V}$ der schon verbundenen Knoten und der andere nicht. Weil der Baum ${\displaystyle T_{1}}$ ein Spannbaum des Graphen ${\displaystyle G}$ ist, gibt es im Baum ${\displaystyle T_{1}}$ einen Pfad, der die beiden Endknoten verbindet. Wenn man den Pfad entlang fahrt, muss man auf eine Kante ${\displaystyle f}$ stoßen, die einen Knoten der Menge ${\displaystyle V}$ mit einem Knoten verbindet, der nicht in der Menge ${\displaystyle V}$ liegt. Bei der Iteration, in der die Kante ${\displaystyle e}$ zu Baum ${\displaystyle T}$ hinzugefugt wurde, konnte nun auch die Kante ${\displaystyle f}$ hinzugefugt worden sein und sie wurde anstelle der Kante ${\displaystyle e}$ hinzugefugt, wenn ihr Gewicht kleiner als das Gewicht von ${\displaystyle e}$ ware, und weil die Kante ${\displaystyle f}$ nicht hinzugefugt wurde, schließen wir daraus, dass ihr Gewicht mindestens so groß ist wie das Gewicht von ${\displaystyle e}$.

Der Baum ${\displaystyle T_{2}}$ sei der Graph, der aus ${\displaystyle T_{1}}$ durch Entfernen der Kante ${\displaystyle f}$ und Hinzufugen der Kante ${\displaystyle e}$ entsteht. Es ist einfach zu zeigen, dass der Baum ${\displaystyle T_{2}}$ zusammenhangend ist, die gleiche Anzahl von Kanten wie der Baum ${\displaystyle T_{1}}$ hat und das Gesamtgewicht seiner Kanten nicht großer als das von Baum ${\displaystyle T_{1}}$ ist, daher ist ${\displaystyle T_{2}}$ auch ein minimaler Spannbaum des Graphen ${\displaystyle G}$ und er enthalt die Kante ${\displaystyle e}$ und alle Kanten, die wahrend der Konstruktion der Menge ${\displaystyle V}$ hinzugefugt wurden. Wiederholt man die bisherigen Schritte, dann erhalt man schließlich einen minimalen Spannbaum des Graphen ${\displaystyle G}$, der mit dem Baum ${\displaystyle T}$ identisch ist. Dies zeigt, dass ${\displaystyle T}$ ein minimaler Spannbaum ist.

Vergleich mit dem Algorithmus von Kruskal [ Bearbeiten | Quelltext bearbeiten ]

Wie auch der Algorithmus von Kruskal , der ebenfalls einen minimal spannenden Baum konstruiert, ist Prims Algorithmus ein Greedy-Algorithmus . Beide Algorithmen beginnen mit einem Graphen ohne Kanten und fugen in jedem Schritt eine Kante mit minimalem Gewicht hinzu. Sie unterscheiden sich vor allem darin, wie die Bildung eines Kreises vermieden wird.

Wahrend der Algorithmus von Kruskal global nach moglichen Kanten mit dem kleinsten Gewicht sucht und bei der Aufnahme dieser Kanten in den Losungsgraph die Kreisbildung aktiv vermeidet, betrachtet der Algorithmus von Prim nur Kanten, die von den Knoten der bisher konstruierten Teilknotenmenge zu Knoten der Komplementarmenge verlaufen. Da aus dieser Kantenmenge eine Kante ausgewahlt wird, vermeidet der Algorithmus per Konstruktion das Auftreten von Kreisen.

Ein Vergleich der Laufzeit der beiden Algorithmen ist schwierig, da im Algorithmus von Prim die Knoten die zentrale Komplexitatsschranke bestimmen, wahrend der Algorithmus von Kruskal auf Basis einer sortierten Kantenliste arbeitet und daher dessen Laufzeit von der Anzahl der Kanten dominiert wird. ^[2]

Parallele Implementierung [ Bearbeiten | Quelltext bearbeiten ]

Der Algorithmus von Prim ist grundlegend sequentieller Natur, da sich die außere Schleife aufgrund von Datenabhangigkeiten zwischen den Iterationen nicht parallelisieren lasst. Es ist allerdings moglich, die extract_min Operation zu parallelisieren. Hierfur kann zum Beispiel eine parallele Implementierung einer Prioritatswarteschlange verwendet werden. Auf einer Parallel Random Access Machine mit insgesamt ${\displaystyle O(|V|)}$ Prozessoren lasst sich der Zugriff auf die Prioritatswarteschlange zu konstanter Zeit beschleunigen ^[3] , sodass sich eine Gesamtlaufzeit in ${\displaystyle O(|E|+|V|)}$ ergibt. Alternativ konnen die Knoten zwischen mehreren Prozessoren aufgeteilt werden, sodass jeder Prozessor die eingehenden Kanten zu seinem Teil der Knoten verwaltet. ^[4] Dies wird in folgendem Pseudocode dargestellt.

1. Weise jedem Prozessor ${\displaystyle P_{i}}$ einen Teil ${\displaystyle V_{i}}$ der Knoten, sowie die dazugehorigen (eingehenden) Kanten zu. Bei Verwendung einer Adjazenzmatrix entspricht dies gerade einem Teil der Spalten.
2. Erstelle auf jedem Prozessor einen Vektor ${\displaystyle C}$, welcher die aktuellen Kosten fur jeden Knoten in ${\displaystyle V_{i}}$ enthalt. Initialisiere diesen Vektor mit ${\displaystyle \infty }$
3. Wiederhole folgende Schritte solange nicht alle Knoten im Spannbaum enthalten sind:
   1. Auf jedem Prozessor: bestimme den Knoten ${\displaystyle v_{i}}$ und dazugehorige Kante ${\displaystyle e_{i}}$ welcher den minimalen Wert in ${\displaystyle C}$ besitzt (lokale Losung).
   2. Bestimme aus den lokalen Losungen den Knoten dessen Verbindung zum aktuellen Spannbaum die geringsten Kosten hat. Dies ist mithilfe einer Minimum-Reduktion uber alle Prozessoren moglich.
   3. Teile jedem Prozessor den gewahlten Knoten mithilfe eines Broadcast mit.
   4. Fuge den neuen Knoten sowie die dazugehorige Kante (es sei denn es handelt sich um den ersten Knoten) dem Spannbaum hinzu
   5. Auf jedem Prozessor: aktualisiere ${\displaystyle C}$ indem die Kanten des neu eingefugten Knotens zu dem eigenen Knotenset betrachtet werden.

Diese Variation von Prims Algorithmus lasst sich sowohl auf Verteilten Systemen , ^[4] auf Shared Memory Systemen ^[5] , sowie auf Grafikprozessoren ^[6] implementieren. Die Laufzeit betragt dabei

${\displaystyle O\left({\frac {|V|^{2}}{|P|}}\right)+O(|V|\log |P|)}$,

da in jeder der ${\displaystyle |V|}$ Iterationen des Algorithmus jeweils ${\displaystyle {\tfrac {|V|}{|P|}}}$ Eintrage betrachtet werden mussen. Zusatzlich wird angenommen, dass sowohl die Minimum-Reduktion als auch der Broadcast in ${\displaystyle O(\log |P|)}$ Zeit durchgefuhrt werden konnen. ^[4]

Als weitere Alternative fur eine parallele Umsetzung von Prims Algorithmus wurde eine Variante prasentiert, in welcher der sequentielle Algorithmus parallel von verschiedenen Startknoten aus ausgefuhrt wird. ^[7] Im Allgemeinen eignen sich andere MST Algorithmen, wie beispielsweise der Algorithmus von Bor?vka , jedoch besser fur eine Parallelisierung.

Programmierung [ Bearbeiten | Quelltext bearbeiten ]

Das folgende Beispiel in der Programmiersprache C# zeigt die Implementierung des Algorithmus von Prim. Bei der Ausfuhrung des Programms wird die Methode Main verwendet, die die Kanten und die Abstande auf der Konsole ausgibt. Die Matrix fur die Abstande wird in einem zweidimensionalen Array vom Datentyp Integer gespeichert. ^[8]

using
 System
;


class
 Program

{

	// Diese Methode gibt den Index des Knotens mit dem minimalen Abstand zum Teilgraphen zuruck

	static
 int
 GetMinimumIndex
(
int
[]
 distances
,
 bool
[]
 includedNodes
)

	{

		int
 minimumDistance
 =
 int
.
MaxValue
;

		int
 minimumIndex
 =
 -
1
;

		for
 (
int
 i
 =
 0
;
 i
 <
 distances
.
Length
;
 i
++
)

		{

			if
 (
!
includedNodes
[
i
]
 &&
 distances
[
i
]
 <
 minimumDistance
)

			{

				minimumDistance
 =
 distances
[
i
];

				minimumIndex
 =
 i
;

			}

		}

		return
 minimumIndex
;

	}

	
	// Diese Methode verwendet den Algorithmus von Prim und gibt den minimalen Spannbaum zuruck

	static
 void
 Prim
(
int
[,]
 distanceMatrix
,
 int
 numberOfNodes
,
 out
 int
[]
 parent
,
 out
 int
[]
 distances
)

	{

		parent
 =
 new
 int
[
numberOfNodes
];

		distances
 =
 new
 int
[
numberOfNodes
];

		bool
[]
 includedNodes
 =
 new
 bool
[
numberOfNodes
];

		for
 (
int
 i
 =
 0
;
 i
 <
 numberOfNodes
;
 i
++
)

		{

			distances
[
i
]
 =
 int
.
MaxValue
;

			includedNodes
[
i
]
 =
 false
;

		}

		distances
[
0
]
 =
 0
;

		parent
[
0
]
 =
 -
1
;

		for
 (
int
 i
 =
 0
;
 i
 <
 numberOfNodes
 -
 1
;
 i
++
)

		{

			int
 minimumIndex
 =
 GetMinimumIndex
(
distances
,
 includedNodes
);

			includedNodes
[
minimumIndex
]
 =
 true
;

			for
 (
int
 j
 =
 0
;
 j
 <
 numberOfNodes
;
 j
++
)

			{

				if
 (
distanceMatrix
[
minimumIndex
,
 j
]
 !=
 0
 &&
 !
includedNodes
[
j
]
 &&
 distanceMatrix
[
minimumIndex
,
 j
]
 <
 distances
[
j
])

				{

					parent
[
j
]
 =
 minimumIndex
;

					distances
[
j
]
 =
 distanceMatrix
[
minimumIndex
,
 j
];

				}

			}

		}

	}

	
	// Hauptmethode, die das Programm ausfuhrt

	public
 static
 void
 Main
()

	{

		int
[,
 ]
 distanceMatrix
 =
 new
 int
[,]
 {
 {
0
,
 2
,
 0
,
 6
,
 0
},

			{
2
,
 0
,
 3
,
 8
,
 5
},

			{
0
,
 3
,
 0
,
 0
,
 7
},

			{
6
,
 8
,
 0
,
 0
,
 9
},

			{
0
,
 5
,
 7
,
 9
,
 0
}
 };
 // Deklariert und initialisiert die Matrix mit den Abstanden zwischen allen Punkten als zweidimensionales Array vom Typ int

		int
[]
 parent
;

		int
[]
 distances
;

		int
 numberOfNodes
 =
 5
;

		Prim
(
distanceMatrix
,
 numberOfNodes
,
 out
 parent
,
 out
 distances
);

		Console
.
WriteLine
(
"Kante\tAbstand"
);
 // Ausgabe auf der Konsole

		for
 (
int
 i
 =
 1
;
 i
 <
 numberOfNodes
;
 i
++
)

		{

			Console
.
WriteLine
(
parent
[
i
]
 +
 " - "
 +
 i
 +
 "\t"
 +
 distanceMatrix
[
i
,
 parent
[
i
]]);
 // Ausgabe auf der Konsole

		}

		
		Console
.
ReadLine
();

	}

}

Literatur [ Bearbeiten | Quelltext bearbeiten ]

• Robert C. Prim : Shortest connection networks and some generalisations . In: Bell System Technical Journal , 36, 1957, S. 1389?1401
• David Cheriton, Robert Tarjan : Finding minimum spanning trees . In: SIAM Journal on Computing , 5, Dezember 1976, S. 724?741
• Ellis Horowitz, Sartaj Sahni : Fundamentals of Computer Algorithms . In: Computer Science Press , 1978, S. 174?183

Weblinks [ Bearbeiten | Quelltext bearbeiten ]

Commons : Algorithmus von Prim  ? Sammlung von Bildern, Videos und Audiodateien

Wikibooks: Algorithmus von Prim  ? Implementierungen in der Algorithmensammlung

• Interaktives Applet zur Lernen, Ausprobieren und Demonstrieren des Algorithmus
• Anschauliche Darstellung des Algorithmus im Rahmen des Informatik Jahres 2006
• Java-Applet zur Schritt-fur-Schritt-Visualisierung (englisch)

Einzelnachweise [ Bearbeiten | Quelltext bearbeiten ]

1. ↑ Gerth Stølting Brodal, Jesper Larsson Traff, Christos D. Zaroliagis: A Parallel Priority Queue with Constant Time Operations . In: Journal of Parallel and Distributed Computing . 49. Jahrgang, Nr.   1 , 1998, S.   4?21 .  
2. ↑ vgl. dazu etwa Ellis Horowitz, Sartaj Sahni: Fundamentals of Computer Algorithms. (s. Literatur)
3. ↑ Gerth Stølting Brodal, Jesper Larsson Traff, Christos D. Zaroliagis: A Parallel Priority Queue with Constant Time Operations . In: Journal of Parallel and Distributed Computing . 49. Jahrgang, Nr.   1 , 1998, S.   4?21 .  
4. ↑ ^{a b c} Ananth Grama, Anshul Gupta, George Karypis, Vipin Kumar: Introduction to Parallel Computing . 2003, ISBN 978-0-201-64865-2 , S.   444?446 .  
5. ↑ Michael J. Quinn, Narsingh Deo: Parallel graph algorithms . In: ACM Computing Surveys (CSUR) 16.3 . 1984, S.   319?348 .  
6. ↑ Wei Wang, Yongzhong Huang, Shaozhong Guo: Design and Implementation of GPU-Based Prim’s Algorithm . In: International Journal of Modern Education and Computer Science 3.4 . 2011.  
7. ↑ Rohit Setia: A new parallel algorithm for minimum spanning tree problem . In: Proc. International Conference on High Performance Computing (HiPC) . 2009.  
8. ↑ GeeksforGeeks: Prim’s Minimum Spanning Tree (MST)